FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
сos(900+α)
sin(900+α)
сos(1800+α)
sin(1800+α)
sin(2700+α)
cos(2700+α)
, 3600+α
Из равенства прямоугольных треугольников можно заключить, что:
cosα=sin(900+ α)=–cos(1800+ α)=–sin(2700+ α)=cos(3600+ α), а также
sinα=–cos(900+ α)=–sin(1800+ α)=cos(2700+ α)=sin(3600+ α).
С первым столбцом все ясно – в нем известные Вам тригонометрические функции. Во втором столбце показано, что любой аргумент(угол) этих функций можно представить в таком виде. Поясним это на конкретных примерах:
Умножьте полученные сумму или разность на и получите искомые выражения.
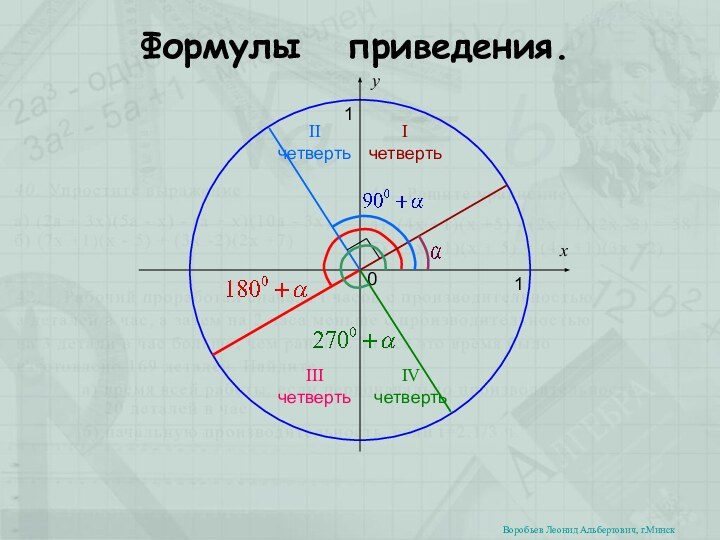
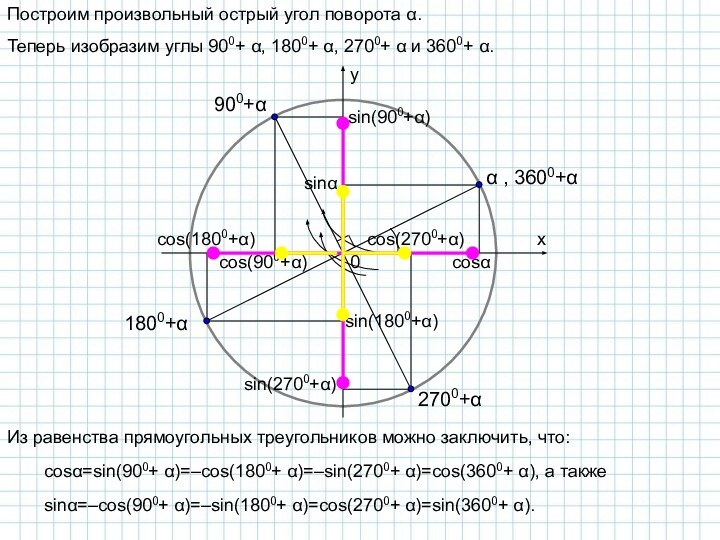
В любом случае мы добились следующего: наш аргумент тригонометрической функции представлен в виде целого числа прямых углов плюс или минус какой-то острый угол.
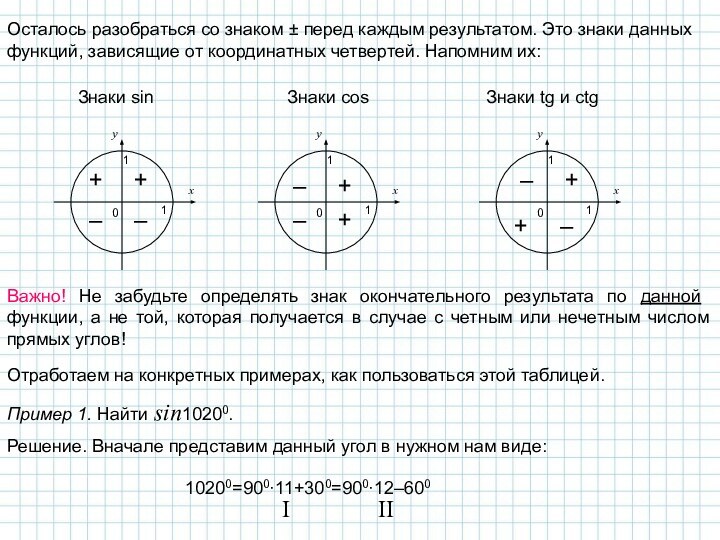
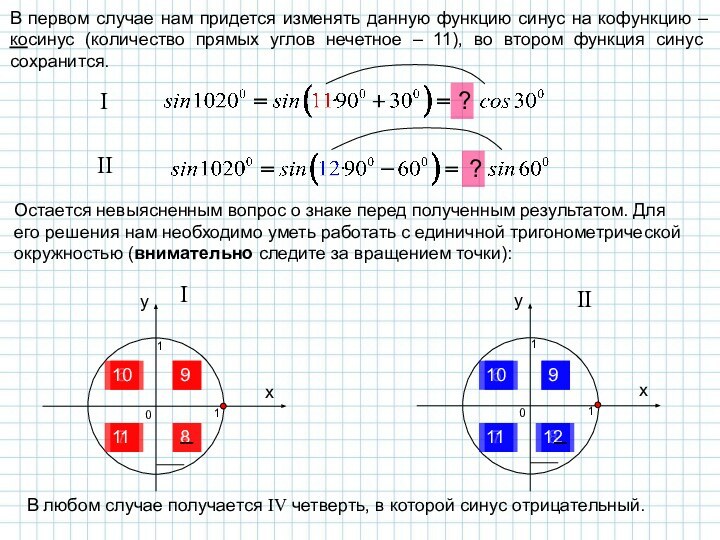
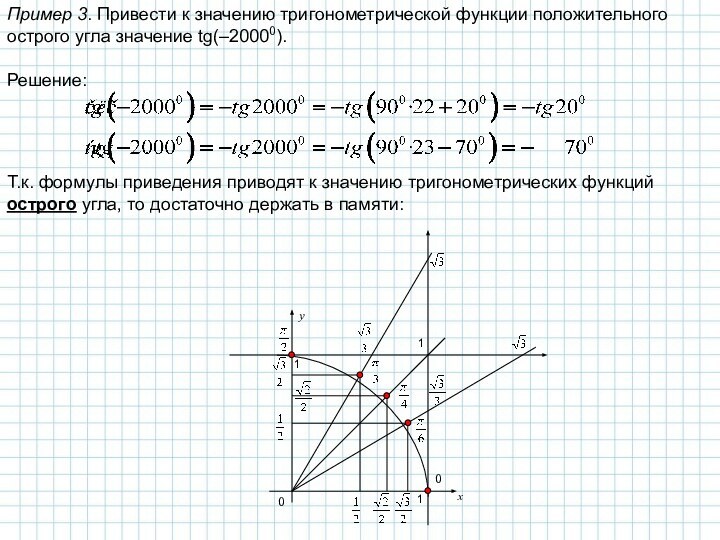
Обратим теперь внимание на 3-й и 4-й столбцы таблицы. Сразу заметим, что в случае четного числа прямых углов тригонометрическая функция остается такой же, а в случае нечетного числа – изменяется на кофункцию (sin на cos, tg на ctg и наоборот), причем аргументом этой функции является остаток.
х
0
у
1
1
х
0
у
1
1
х
0
у
1
1
Знаки sin
Знаки cos
Знаки tg и ctg
+
+
+
+
+
+
–
–
–
–
–
–
Важно! Не забудьте определять знак окончательного результата по данной функции, а не той, которая получается в случае с четным или нечетным числом прямых углов!
Отработаем на конкретных примерах, как пользоваться этой таблицей.
Пример 1. Найти sin10200.
Решение. Вначале представим данный угол в нужном нам виде:
10200=900·11+300=900·12–600
I
II
I
II
Остается невыясненным вопрос о знаке перед полученным результатом. Для его решения нам необходимо уметь работать с единичной тригонометрической окружностью (внимательно следите за вращением точки):
?
?
х
у
0
1
1
х
у
0
1
1
I
II
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
12
В любом случае получается IV четверть, в которой синус отрицательный.
–
–
