- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Клуб веселых математиков
Содержание
- 2. Цель внеклассного мероприятияУглубление и расширение учебного материала;Привитие
- 3. «Тем, кто учит математику,Тем, кто учит математике,Тем,
- 4. «Математик должен быть поэтом в душе»(С.В.Ковалевская)
- 5. «…Математику уже затем учить следует, что она ум в порядок приводит» (М.В.Ломаносов)
- 6. Краткая историческая справка о Евклиде и Лобачевском
- 7. ЕвклидДревнегреческий математик(умер между 275 и 270 г. до н. э.)
- 8. Евклид (Eνκλειδηζ), древнегреческий математик, авторпервого из дошедших
- 9. ЛОБАЧЕВСКИЙ Николай Иванович (1793-1856),российский математик, создатель неевклидовой геометрии (геометрии Лобачевского) . Ректор Казанского университета (1827-46).
- 10. Лобачевский, Николай Иванович родился 22 октября 1793
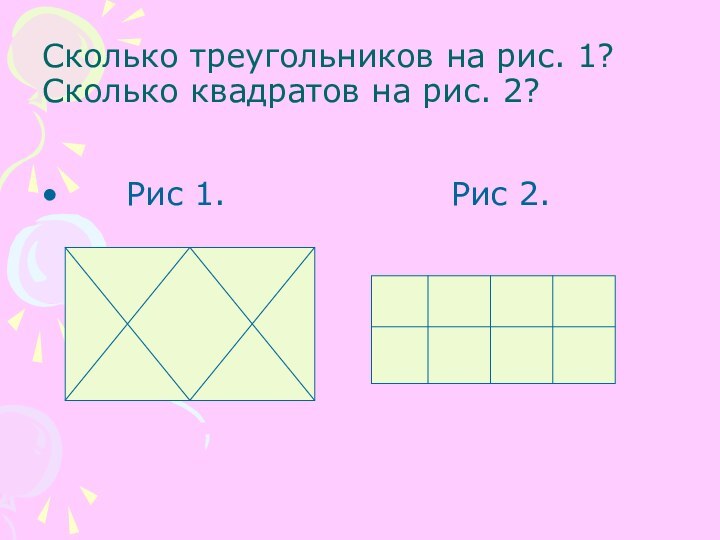
- 11. Сколько треугольников на рис. 1? Сколько квадратов
- 12. Задача.Разрезать прямоугольный треугольник на такие три части,
- 13. Скачать презентацию
- 14. Похожие презентации
Цель внеклассного мероприятияУглубление и расширение учебного материала;Привитие учащимся практических навыков;Ознакомление детей с историей развития математики;Использование материалов по занимательной математике.












Слайд 2
Цель внеклассного мероприятия
Углубление и расширение учебного материала;
Привитие учащимся
практических навыков;
занимательной математике.
Слайд 3
«Тем, кто учит математику,
Тем, кто учит математике,
Тем, кто
любит математику,
Тем, кто еще не знает, что может любить
математику,Неделя математики посвящается.»
Слайд 8
Евклид (Eνκλειδηζ), древнегреческий математик, автор
первого из дошедших до
нас теоретических трактатов
по математике.
Сведения об Евклиде крайне скудны.
Достоверным
можно считать лишь то, что егонаучная деятельность протекала в Александрии в III
веке до н. э. Евклид – первый математик
александрийской школы. Его главная работа
«Начала» (в латинизированной форме – «Элементы»)
содержит изложение планиметрии, стереометрии и
ряда вопросов теории чисел ; в ней он подвел итог
предшествующему развитию греческой математики и
создал фундамент дальнейшего развития математики.
Слайд 9
ЛОБАЧЕВСКИЙ Николай Иванович
(1793-1856),
российский математик, создатель неевклидовой геометрии
(геометрии Лобачевского) .
Ректор Казанского университета (1827-46).
Слайд 10
Лобачевский, Николай Иванович родился 22 октября 1793 г.
в
Нижегородской губернии. Учился в Казанском университете; рано
обратил на себя
внимание успехами в математике.Лобачевский читал лекции по самым разнообразным отделам
математики, а также по физике и астрономии.
Громкая слава Лобачевского основана на его геометрических
изысканиях, начатых в 1814 - 1817 годах. Сохранившаяся запись
лекций Лобачевского, читанных в эти годы, показывает, что
первоначально Лобачевский стоял на традиционной точке зрения,
предлагая разные доказательства аксиомы параллельных линий.
К 1826 г. он пришел к определенной формулировке своей новой
геометрической системы, которую назвал "воображаемой
геометрией" в отличие от "употребительной", евклидовой
Открытие Лобачевского (1826, опубликованное 1829-30), не
получившее признания современников, совершило переворот в
представлении о природе пространства, в основе которого более 2
тыс. лет лежало учение Евклида, и оказало огромное влияние на
развитие математического мышления.
Слайд 12
Задача.
Разрезать прямоугольный треугольник на такие три части, что
бы из них можно было бы составить фигуры, изображенные
на рисунке.





























