- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕСИИ
Содержание
- 2. 1. Нелинейные модели регрессии Во многих практических
- 3. Многие экономические зависимости не являются линейными по
- 4. Различают два класса нелинейных регрессий: 1) регрессии, нелинейные
- 5. Равносторонняя гипербола 2)
- 6. Показательная ЭкспоненциальнаяНелинейная регрессия по включенным переменным не таит
- 7. Так, например, в полиноме второй степени заменив
- 8. *Ее решение можно найти методом Крамера.
- 9. Среди класса нелинейных функций, параметры которых легко
- 10. Заменив в уравнении равносторонней гиперболы 1/х на
- 11. Модели виданазываются полулогарифмическими моделями. Эти модели
- 12. Система нормальных уравнений, например, для второй модели
- 13. В этом случае система нормальных уравнений для
- 14. Если нелинейная модель внутренне линейна, то
- 15. Данная модель нелинейна относительно оцениваемых параметров, так
- 16. Оценка параметров a и b в полученном
- 17. Параметр b определяется непосредственно из системы, а
- 18. Для степенной функции коэффициент эластичности будет рассчитываться следующим образомПри b0 – предложения.
- 19. В других функциях коэффициент эластичности зависит от
- 20. Если же модель степенной регрессии представить
- 21. Модели внутренне нелинейные по параметрам могут иметь
- 22. Линеаризовать эту модель можно относительно переменной Для
- 23. Так называемая логистическая функция также может быть приведена к линейному виду: Переходя к обратным величинам, получим:
- 24. Перенесем единицу в левую часть и прологарифмируем по основанию е, получим:или
- 25. 2. Модели с распределенным лагом.Будем рассматривать динамические
- 26. Будем рассматривать модели, в которых значения переменных
- 27. Если значение результативного признака в текущий момент
- 28. Разработка экономической политики как на макро-, так
- 29. Эконометрическое моделирование охарактеризованных выше процессов осуществляется с
- 30. Наряду с лаговыми значениями независимых, или факторных,
- 31. Построение моделей с распределенным лагом и моделей
- 32. Во-вторых, исследователям приходится решать проблемы выбора оптимальной
- 33. 3. Лаги Алмон. Рассмотрим общую модель с
- 34. Коэффициент регрессии b0 при переменной xt характеризует
- 35. В момент (t + 1) совокупное воздействие
- 36. С учетом конечной величины лага можно сказать,
- 37. Он показывает абсолютное изменение результата у в
- 38. Предположим, что было установлено, что в исследуемой
- 39. Формально модель зависимости коэффициентов bj от величины
- 40. В наиболее общем виде для полинома k-ой
- 41. b0 = c0; b1 =
- 42. Подставив в (1) найденные соотношения для bj,
- 43. Обозначим слагаемые в скобках при сi как
- 44. Перепишем модель (4) с учетом соотношений (5):yt
- 45. Процедура применения метода Алмон для расчета параметров
- 46. Определяются параметры уравнения линейной регрессии (6).С помощью соотношений (2) рассчитываются параметры исходной модели с распределенным лагом.
- 47. Применение метода Алмон сопряжено с рядом проблем.1.
- 48. Влияние этого фактора в такой модели будет
- 49. Выбор большей величины лага по сравнением с
- 50. Наиболее простым способом определения реальной величины лага
- 51. 2. Необходимо установить степень полинома k. Обычно
- 52. 3. Переменные z, которые определяются как линейные
- 53. Однако мультиколлинеарность факторов z0, … , zk
- 54. Метод Алми имеет два преимущества.1. Он достаточно
- 55. 4. Модель Койка. Рассмотренные модели были построены
- 56. Параметры такой модели обычным МНК определить нельзя
- 57. Впервые такой подход к оценке параметров моделей
- 58. Для некоторого периода (t – l) это
- 59. Чем ближе λ к нулю, тем выше
- 60. Выразим с помощью (8) все коэффициенты bj
- 61. Вычтем найденное соотношение (11) из соотношения (9):yt
- 62. Полученная модель есть модель двухфакторной линейной регрессии
- 63. Описанный алгоритм получил название преобразования Койка. Это
- 64. Несмотря на бесконечное число лаговых переменных в
- 65. то средний лаг определяется как (15)
- 66. Нетрудно заметить, что при λ = 0,5
- 67. выполнение следующего условия:Поэтому медианный лаг в модели Койка равен
- 68. *
- 69. *
- 70. *
- 71. *
- 72. *
- 73. *
- 74. *
- 75. Скачать презентацию
- 76. Похожие презентации
1. Нелинейные модели регрессии Во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат и может использоваться для анализа и прогнозирования. Однако в силу многообразия и сложности экономических процессов ограничиться рассмотрением лишь линейных








































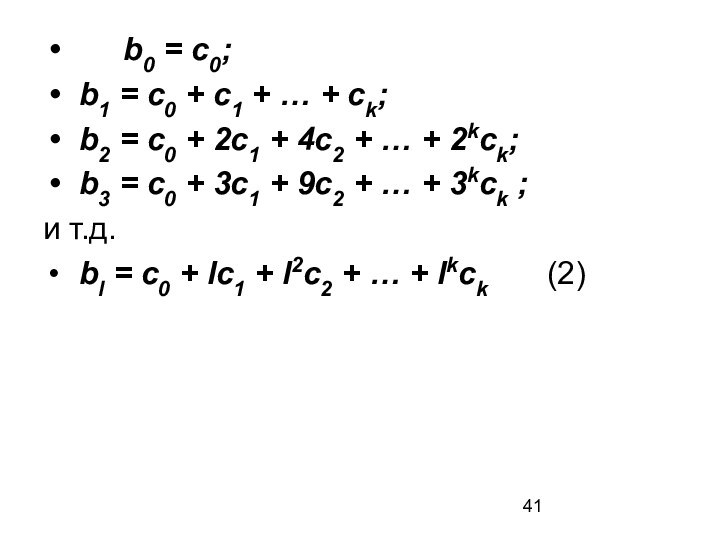


































Слайд 3 Многие экономические зависимости не являются линейными по своей
сути, и поэтому их моделирование линейными функциями, безусловно, не
даст положительного результата. Так, например, нелинейными являются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства - трудом, капиталом и т.п.), функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом) и др.
Слайд 4
Различают два класса нелинейных регрессий:
1) регрессии, нелинейные относительно
включенных в анализ объясняющих переменных, но линейные по оцениваемым
параметрам. К таким функциям относятся квазилинейные функции.Например, это полиномы различных степеней
Слайд 5
Равносторонняя гипербола
2) регрессии нелинейные
по оцениваемым параметрам. К таким регрессиям относятся нелинейные функции
второго класса.Например, степенная функция
Слайд 6
Показательная
Экспоненциальная
Нелинейная регрессия по включенным переменным не таит каких-либо
сложностей в оценке ее параметров.
Она определяется, как и
в линейной регрессии, методом наименьших квадратов, так как эти функции линейны по параметрам.
Слайд 7
Так, например, в полиноме второй степени
заменив х
= х1, х2 = х2, получим двухфакторное уравнение линейной
регрессии: у = a0 + a1x1 + a2x2 + ε.Применив метод наименьших квадратов для оценки коэффициентов исходного полинома второй степени, получим следующую систему нормальных уравнений:
Слайд 9 Среди класса нелинейных функций, параметры которых легко оцениваются
с помощью МНК, следует назвать хорошо известную в эконометрике
равностороннюю гиперболу:Она может быть использована для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота.
Слайд 10 Заменив в уравнении равносторонней гиперболы 1/х на z,
получим уравнение линейной регрессии y = a + bz
+ e, оценка параметров которого может быть дана с помощью МНК.Система нормальных уравнений для этого случая примет вид:
Слайд 11
Модели вида
называются полулогарифмическими моделями. Эти модели также относятся
к нелинейным моделям относительно включенных в анализ объясняющих переменных,
но линейным по параметрам.Слайд 12 Система нормальных уравнений, например, для второй модели будет
иметь вид:
Возможны и другие модели, нелинейные относительно объясняющих переменных.
Например,
Слайд 13 В этом случае система нормальных уравнений для оценки
параметров примет вид:
Иначе обстоит дело с регрессией, нелинейной по
оцениваемым параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные.
Слайд 14 Если нелинейная модель внутренне линейна, то она с
помощью соответствующих преобразований может быть приведена к линейному виду.
Например, в экономических исследованиях при изучении эластичности спроса от цен широко используется степенная функциягде y – спрашиваемое количество;
х – цена;
ε – случайная ошибка.
Слайд 15 Данная модель нелинейна относительно оцениваемых параметров, так как
включает параметры а и b неаддитивно. Однако ее можно
считать внутренне линейной, так как логарифмирование данного уравнения, например, по основанию e приводит его к видуСлайд 16 Оценка параметров a и b в полученном уравнении
может быть произведена с помощью МНК. При этом решается
система нормальных уравнений:
Слайд 17 Параметр b определяется непосредственно из системы, а параметр
а – косвенным путем после потенцирования величины lna.
Наибольшее распространение
степенной функции в эконометрике связано с тем, что параметр b имеет четкое экономическое истолкование, – он является коэффициентом эластичности. Это значит, что коэффициент b показывает, на сколько % в среднем изменится результат, если фактор изменится на 1%. Слайд 18 Для степенной функции коэффициент эластичности будет рассчитываться следующим
образом
При b0 –
предложения.Слайд 19 В других функциях коэффициент эластичности зависит от значений
фактора x. В силу этого для них обычно рассчитывается
средний показатель эластичности
Слайд 20
Если же модель степенной регрессии представить в виде
то
она становится внутренне нелинейной, так как ее невозможно превратить
в линейный вид. В этом случае, то есть, если модель внутренне нелинейна по параметрам, используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.Слайд 21 Модели внутренне нелинейные по параметрам могут иметь место
в эконометрических исследованиях, однако гораздо большее распространение получили модели,
приводимые к линейному виду.Среди них, в частности, можно назвать модель обратной зависимости вида
Слайд 22
Линеаризовать эту модель можно относительно переменной
Для
этого нужно просто «перевернуть» дробь:
Вводя новую переменную Y =
получим линейное уравнение:
Y = a + bx + ε.
Слайд 23 Так называемая логистическая функция также может быть приведена
к линейному виду:
Переходя к обратным величинам, получим:
Слайд 25
2. Модели с распределенным лагом.
Будем рассматривать динамические эконометрические
модели. Эконометрическая модель является динамической, если в данный момент
времени t она учитывает значения входящих в нее переменных, относящиеся как к текущим, так и к предыдущим моментам времени, т.е. если эта модель отражает динамику исследуемых переменных в каждый момент времени.
Слайд 26
Будем рассматривать модели, в которых значения переменных за
прошлые периоды времени (лаговые переменные) непосредственно включены в модель
(присутствуют в явном виде). Это модели с распределенным лагом.
Слайд 27
Если значение результативного признака в текущий момент времени
t формируется под воздействием ряда факторов, действовавших в прошлые
моменты времени t – 1, t – 2, … , t – l, то величину l, характеризующую запаздывание в воздействии фактора на результат, называют лагом, а временные ряды самих факторных переменных, сдвинутые на один или более моментов времени, – лаговыми переменными.
Слайд 28
Разработка экономической политики как на макро-, так и
на микроуровне требует решения обратного типа задач, т.е. задач,
определяющих, какое воздействие окажут значения управляемых переменных текущего периода на будущие значения экономических показателей.
Слайд 29
Эконометрическое моделирование охарактеризованных выше процессов осуществляется с применением
моделей, содержащих не только текущие, но и лаговые значения
факторных переменных. Эти модели называются моделями с распределенным лагом.Например,
yt = a + b0xt + b1xt-1 + b2xt-2 + εt –
модель с распределенным лагом.
Слайд 30
Наряду с лаговыми значениями независимых, или факторных, переменных
на величину зависимой переменной текущего периода могут оказывать влияние
ее значения в прошлые моменты или периоды времени. Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии. Например, модель видаyt = a + b0xt + c1yt-1 + εt –
модель авторегрессии.
Слайд 31
Построение моделей с распределенным лагом и моделей авторегрессии
имеет свою специфику. Во-первых, оценка параметров модели авторегрессии, а
в большинстве случаев и моделей с распределенным лагом не может быть произведена с помощью обычного МНК ввиду нарушения его предпосылок и требует специальных статистических методов.
Слайд 32
Во-вторых, исследователям приходится решать проблемы выбора оптимальной величины
лага и определения его структуры.
Наконец, в-третьих, между моделями
с распределенным лагом и моделями авторегрессии существует определенная взаимосвязь, и в некоторых случаях необходимо осуществлять переход от одного типа моделей к другому.
Слайд 33
3. Лаги Алмон. Рассмотрим общую модель с распределенным
лагом, имеющую конечную максимальную величину лага l, которая описывается
соотношениемyt = a + b0xt + b1xt-1 + … + bpxt-p + εt (1)
Эта модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной х, то это изменение будет влиять на значения переменной у в течение l следующих моментов времени.
Слайд 34
Коэффициент регрессии b0 при переменной xt характеризует среднее
абсолютное изменение yt при изменении xt на 1 ед.
своего измерения в некоторый фиксированный момент времени t без учета воздействий лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.
Слайд 35
В момент (t + 1) совокупное воздействие факторной
переменной xt на результат уt составит (b0 + b1)
усл. ед., в момент (t + 2) это воздействие составит (b0 + b1 + b2) и т.д. Полученные таким образом суммы называют промежуточными мультипликаторами.
Слайд 36
С учетом конечной величины лага можно сказать, что
изменение переменной xt в момент t на 1 усл.
ед. приведет к общему изменению результата через l моментов времени на (b0 + b1 + … +bl) абсолютных единиц.Величину
b = b0 + b1 + … + bl
называют долгосрочным мультипликатором.
Слайд 37
Он показывает абсолютное изменение результата у в долгосрочном
периоде
t + l под влиянием изменения фактора х
на 1 ед.
Слайд 38
Предположим, что было установлено, что в исследуемой модели
имеет место полиномиальная структура лага, т.е. зависимость коэффициентов регрессии
bi от величины лага описывается полиномом k-ой степени. Частным случаем полиномиальной структуры лага является линейная модель. Лаги, структуру которых можно описать с помощью полиномов, называют лагами Алмон, по имениШ. Алмон, впервые обратившей внимание на такое представление лагов.
Слайд 39
Формально модель зависимости коэффициентов bj от величины лага
j в форме полинома можно записать в следующем виде:
–
для полинома 1-й степени: bj = c0 + c1j;
– для полинома 2-й степени:
bj = c0 + c1j + с2j2;
– для полинома 3-й степени:
bj = c0 + c1j + с2j2 + c3j3 и т.д.
Слайд 40
В наиболее общем виде для полинома k-ой степени
имеем:
bj = c0 + c1j + с2j2 + …
+ ckjk .Тогда каждый из коэффициентов модели (1) можно выразить следующим образом:
Слайд 41
b0 = c0;
b1 = c0
+ c1 + … + ck;
b2 = c0 +
2c1 + 4c2 + … + 2kck;b3 = c0 + 3c1 + 9c2 + … + 3kck ;
и т.д.
bl = c0 + lc1 + l2c2 + … + lkck (2)
Слайд 42
Подставив в (1) найденные соотношения для bj, получим:
yt
= a + c0xt + (c0 + c1 +
… + ck)xt-1 +(c0 + 2c1 + 4c2 + … + 2kck)xt-2 + ( c0 + 3c1 + 9c2 + … + 3kck)xt-3 + … +( c0 + lc1 + l2c2 + … + lkck)xt-l + εt . (3)
Перегруппируем слагаемые в (3):
yt = a + c0(xt + xt-1 + xt-2 + … + xt-l) +
c1(xt-1 + 2xt-2 + 3xt-3 + … + lxt-l) + c2(xt-1 + 4xt-2 + 9xt-3 + … + l2xt-l) + … + ck(xt-1 + 2kxt-2 + 3kxt-3 + … + lkxt-l) + εt . (4)
Слайд 43
Обозначим слагаемые в скобках при сi как новые
переменные:
z0 = xt + xt-1 + xt-2 + …
+ xt-l = z1 = xt-1 + 2xt-2 + 3xt-3 + … + lxt-l =
z2 = xt-1 + 4xt-2 + 9xt-3 + … + l2xt-l = (5)
……………………………………………….
zk = xt-1 + 2kxt-2 + 3kxt-3 + … + l2xt-l =
Слайд 44
Перепишем модель (4) с учетом соотношений (5):
yt =
a + c0z0 + c1z1 + c2z2 + …
+ ckzk + εt 6)
Слайд 45
Процедура применения метода Алмон для расчета параметров модели
с распределенным лагом
1. Определяется максимальная величина лага l.
2. Определяется
степень полинома k, описывающего структуру лага.3. По соотношениям (5) рассчитываются значения переменных
z0, … ,zk.
Слайд 46
Определяются параметры уравнения линейной регрессии (6).
С помощью соотношений
(2) рассчитываются параметры исходной модели с распределенным лагом.
Слайд 47
Применение метода Алмон сопряжено с рядом проблем.
1. Величина
лага l должна быть известна заранее. При ее определении
лучше исходить из максимально возможного лага, чем ограничиваться лагами небольшой длины. Выбор меньшего лага, чем его реальное значение, приведет к тому, что в модели регрессии не будет учтен фактор, оказывающий значительное влияние на результат, т.е. к неверной спецификации модели.
Слайд 48
Влияние этого фактора в такой модели будет выражено
в остатках. Тем самым в модели не будут соблюдаться
предпосылки МНК о случайности остатков, а полученные оценки ее параметров окажутся неэффективными и смещенными.
Слайд 49
Выбор большей величины лага по сравнением с ее
реальным значением будет означать включение в модель статистически незначимого
фактора и снижение эффективности полученных оценок, однако эти оценки все же будут несмещенными.
Слайд 50
Наиболее простым способом определения реальной величины лага является
измерение тесноты связи между результатом и лаговыми значениями фактора.
Кроме того, оптимальную величину лага можно приближенно определить на основе априорной информации экономической теории или проведенных ранее эмпирических исследований.
Слайд 51
2. Необходимо установить степень полинома k. Обычно на
практике ограничиваются рассмотрением полиномов 2-й и 3-й степени, применяя
следующее правило: выбранная степень полинома должна быть на единицу больше числа экстремумов в структуре лага. Если априорную информацию о структуре лага получить невозможно, величину k проще всего получить путем сравнения моделей, построенных для различных значений k, и выбора наилучшей модели.
Слайд 52
3. Переменные z, которые определяются как линейные комбинации
исходных переменных х, будут коррелировать между собой в случаях,
когда наблюдается высокая связь между самими исходными переменными. Поэтому оценку параметров модели (6) приходится проводить в условиях мультиколлинеарности факторов.
Слайд 53
Однако мультиколлинеарность факторов z0, … , zk в
модели (6) сказывается на оценках параметров
b0, … ,
bl в несколько меньшей степени, чем если бы эти оценки были получены путем применения обычного МНК непосредственно к модели (1) в условиях мультиколлинеарности факторов xt, … , xt-l.
Слайд 54
Метод Алми имеет два преимущества.
1. Он достаточно универсален
и может быть применен для моделирования процессов, которые характеризуются
разнообразными структурами лагов.2. При относительно небольшом количестве переменных в (6) (обычно выбирают k = 2 или k = 3), которое не приводит к потере значительного числа степеней свободы, с помощью метода Алмон можно построить модели с распределенным лагом любой длины.
Слайд 55
4. Модель Койка. Рассмотренные модели были построены в
предположении конечной длины лага l.
Предположим, что для описания
некоторого процесса используется модель с бесконечным лагом вида yt = a + b0xt + b1xt-1 + b2xt-2 + … + εt. (7)
Слайд 56
Параметры такой модели обычным МНК определить нельзя из-за
бесконечного числа факторов. Однако, приняв определенные допущения относительно структуры
лага, оценки ее параметров все же можно получить. Эти допущения состоят в наличии геометрической структуры лага, т.е. такой структуры, когда воздействия лаговых значений фактора на результат уменьшаются с увеличением величины лага в геометрической прогрессии.
Слайд 57
Впервые такой подход к оценке параметров моделей с
распределенным лагом был предложен Л.М. Койком. Койк предположил, что
существует некоторый постоянный темп λ (0 < λ < 1) уменьшения во времени лаговых воздействий фактора на результат. Если, например, в период t результат изменялся под воздействием изменения фактора в этот же период времени на b0 ед., то под воздействием изменения фактора, имевшего место в период (t – 1), результат изменится на b0λ ед.; в период (t – 2) – на b0λ2 ед., и т.д.
Слайд 58
Для некоторого периода (t – l) это изменение
результата составит b0λl ед. В более общем виде можно
записать:bj = b0 λ; j = 0, 1, 2, … , 0<λ<1 (8)
Ограничение на значения λ > 0 обеспечивает одинаковые знаки для всех коэффициентов bj > 0, а ограничение bj < 1 означает, что с увеличением лага значения параметров модели ( 7) убывают в геометрической прогрессии.
Слайд 59
Чем ближе λ к нулю, тем выше темп
снижения воздействия фактора на результат во времени и тем
большая доля воздействия на результат приходится на текущие значения фактора хt.
Слайд 60
Выразим с помощью (8) все коэффициенты bj в
модели (7) через b0 и λ:
yt = a +
b0xt + b0 λxt-1 + b0 λ2xt-2 + … + εt (9)Тогда для периода (t – 1) модель (9) можно записать следующим образом:
yt-1 = a + b0xt-1 + b0λxt-2 + b0λ2xt-3 + … + εt-1 10)
Умножим обе части (10) на λ:
λyt-1 =λ a + b0 λxt-1 + b0λ2 xt-2 + b0λ3 xt-3 + …
+λ εt-1 (11)
Слайд 61
Вычтем найденное соотношение (11) из соотношения (9):
yt –
λyt-1 = a – λa + b0 xt +
εt-1 - λ εt-1 (12)Преобразовав (12), получим модель Койка:
yt = a(1 – λ) + b0 xt + (1 – λ)yt-1 + ut , (13)
где ut = εt – λεt-1.
Слайд 62
Полученная модель есть модель двухфакторной линейной регрессии (точнее
– авторегрессии). Определив ее параметры, мы найдем λ и
оценки параметров а и b0 исходной модели. Далее с помощью соотношений (8) можно определить параметры b1, b2, … модели (7). Отметим, что применение обычного МНК к оценке параметров модели (13) приведет к получению смещенных оценок ее параметров ввиду наличия в этой модели в качестве фактора лаговой результативной переменной yt-1.
Слайд 63
Описанный алгоритм получил название преобразования Койка. Это преобразование
позволяет перейти от модели с бесконечными распределенными лагами к
модели авторегрессии, содержащей две независимые переменные: xt и yt-1.
Слайд 64
Несмотря на бесконечное число лаговых переменных в модели
(7), геометрическая структура лага позволяет определить величины среднего и
медианного лагов в модели Койка. Поскольку сумма коэффициентов регрессии в модели (7) есть сумма геометрической прогрессии, т.е.(14)
Слайд 66
Нетрудно заметить, что при λ = 0,5 средний
лаг ,
а при l < 0,5 средний
лаг , т.е. воздействие фактора на результат в среднем занимает менее одного периода времени. Величину (1 – λ) интерпретируют обычно как скорость, с которой происходит адаптация результата во времени к изменению факторного признака. Для расчета медианного лага необходимо