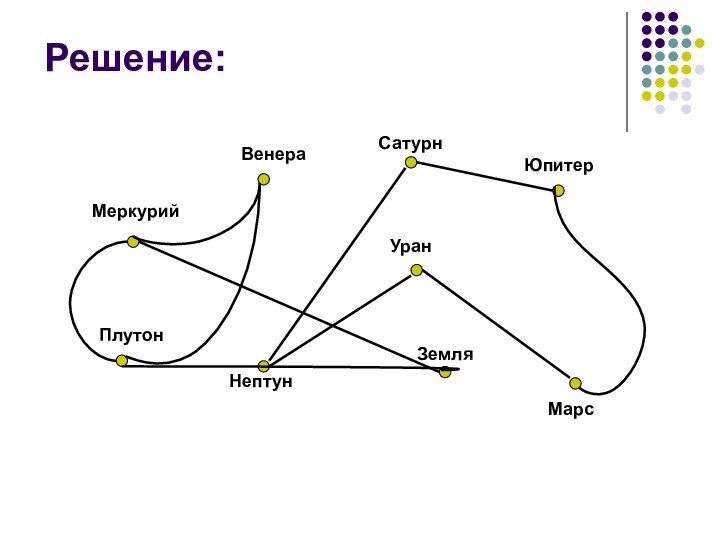
установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам:
Земля-Меркурий
Плутон-
ВенераЗемля – Плутон
Плутон – Меркурий
Меркурий – Венера
Уран – Нептун
Нептун – Сатурн
Сатурн – Юпитер
Юпитер – Марс
Марс – Уран
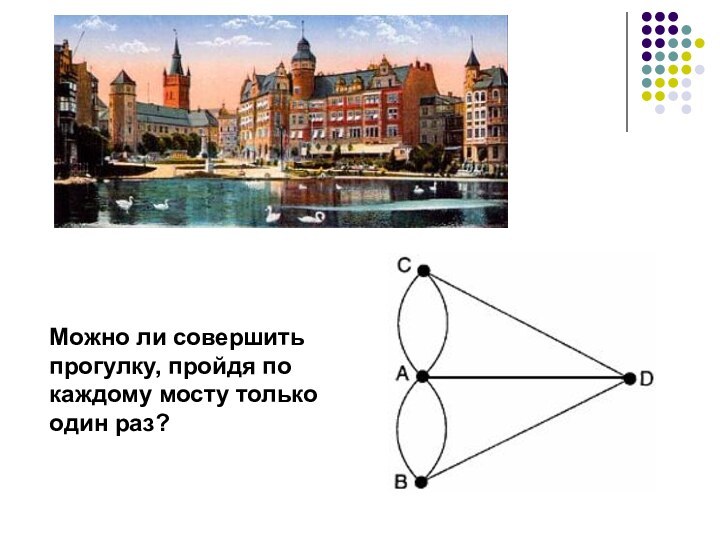
Можно ли долететь на рейсовых ракетах с Земли до Марса ?