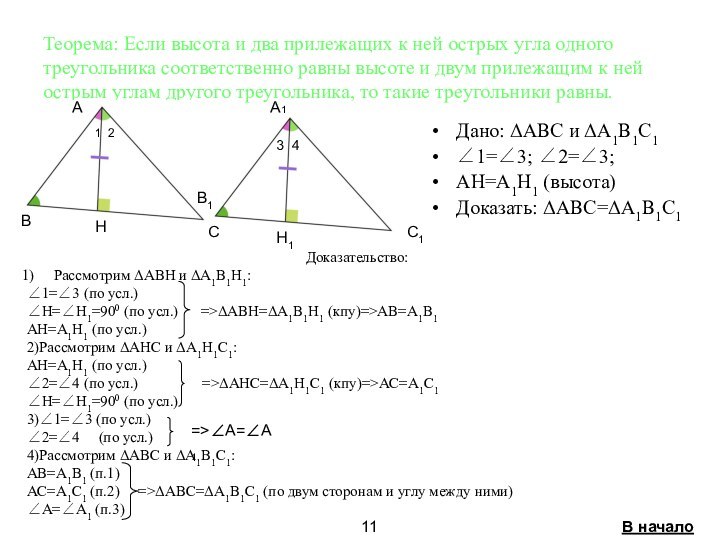
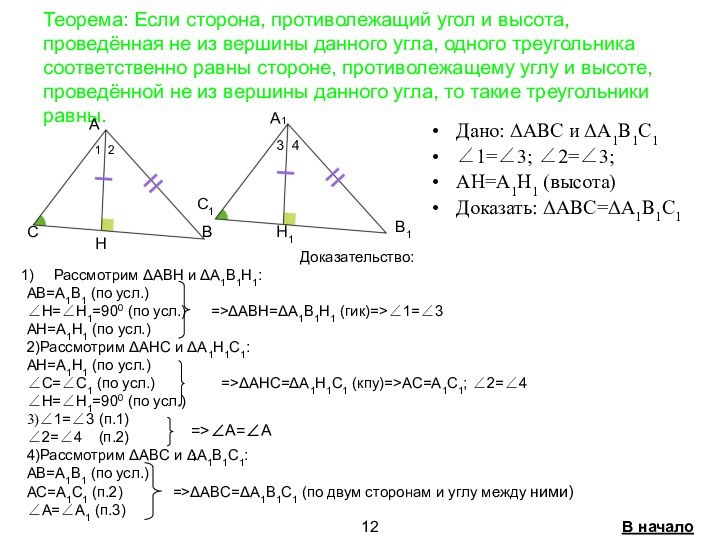
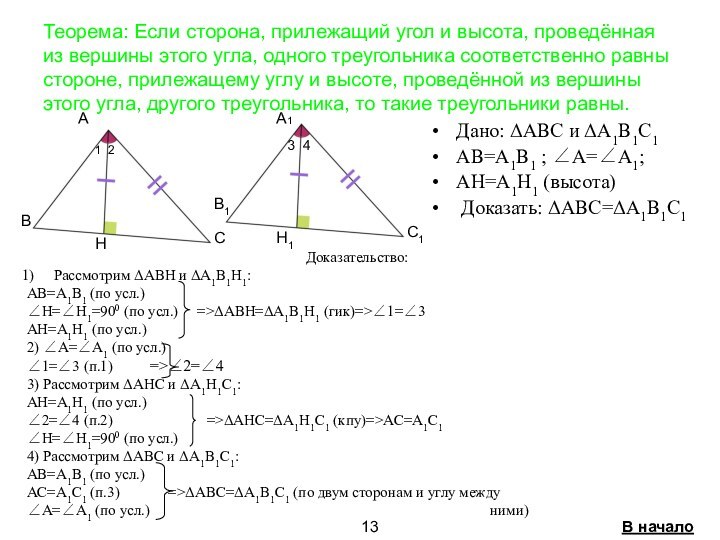
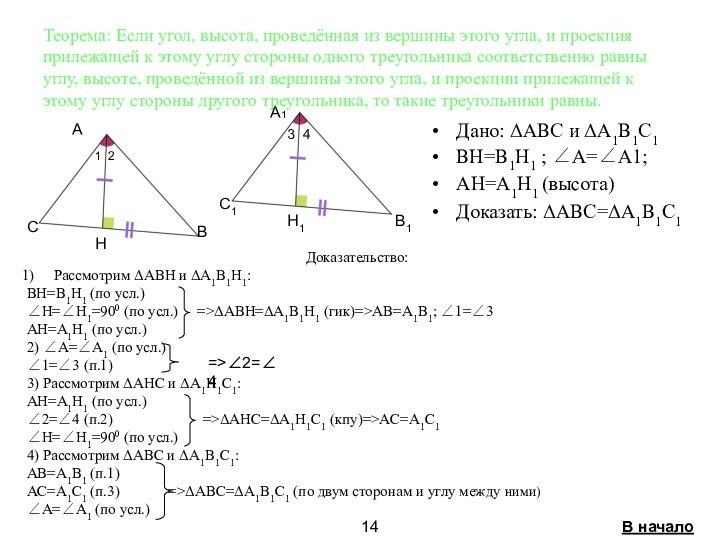
треугольников связанные с
высотой стр. 8-14
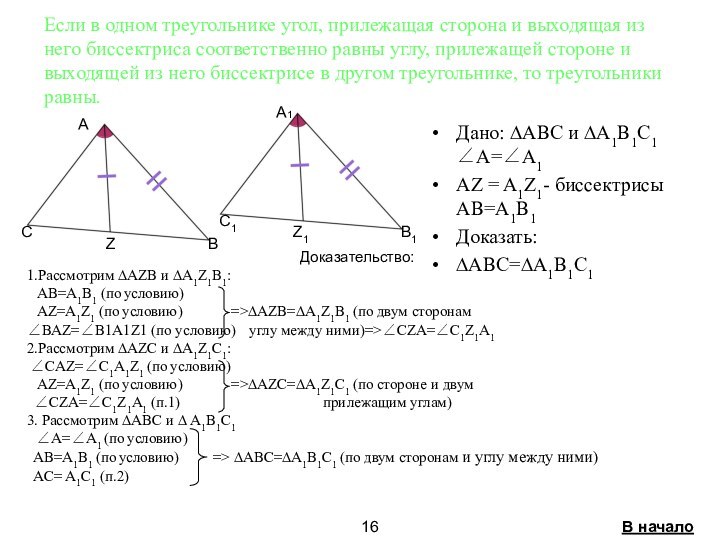
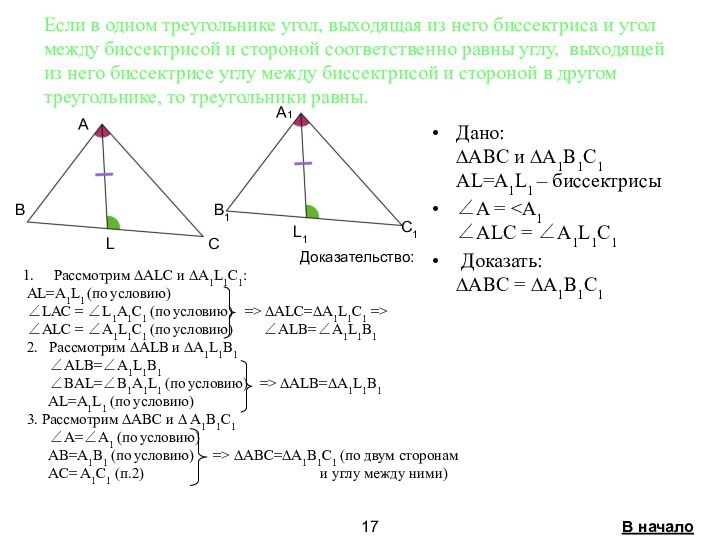
4.Признаки равенства треугольников связанные с
биссектрисой стр. 15-17
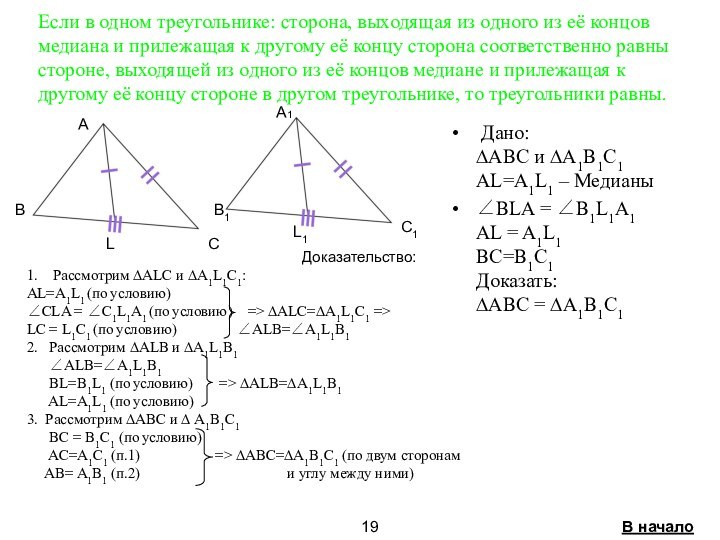
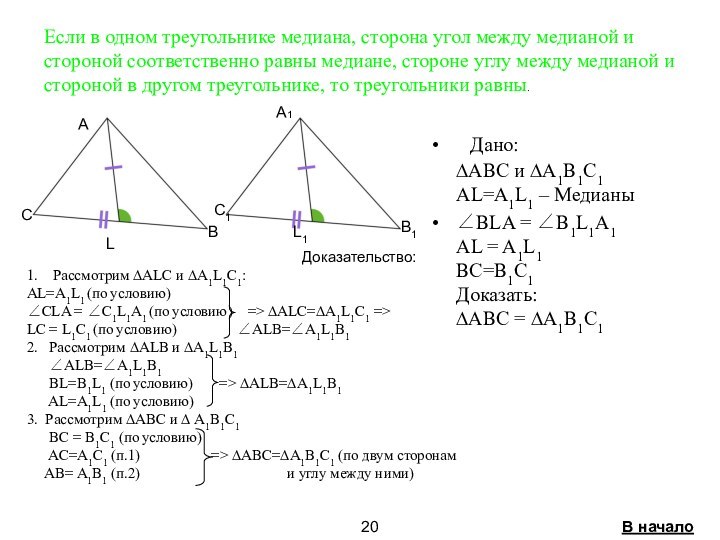
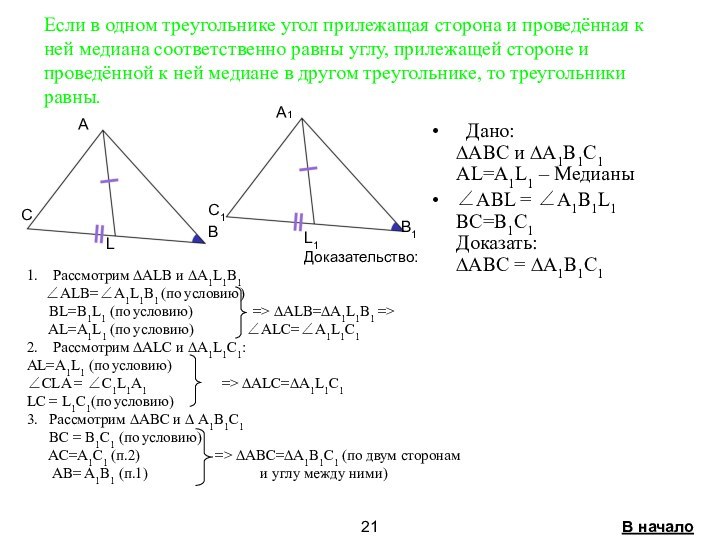
5.Признаки равенства треугольников связанные с
медианой стр. 18-21
4.Литература стр. 22-23
5.Рецензия стр. 24
В начало