- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Использование дидактических игр на уроках математики
Содержание
- 2. “Истинный педагог постарается сделать учение занимательным, но
- 3. Возникновение интереса к математике у большинства учащихся
- 4. Немаловажная роль здесь отводится дидактическим играм на
- 5. На своих уроках учитель всегда
- 6. Игра – творчество, игра – труд. В
- 7. Даже самые пассивные из детей включаются в
- 8. Предмет математики настолько серьезен, что полезно не упускать возможности сделать его немного более занимательным. Б.Паскаль
- 9. На своих уроках математики использую задания, большинство
- 10. Например, при изучении темы «Сложение и вычитание
- 13. Такого рода задания создают в классе атмосферу
- 16. Занимательная форма многих заданий привлекает учащихся, побуждает
- 17. Выполните преобразования. Используя найденные ответы, запишите
- 18. Что такое функция?
- 19. Груша тяжелее, чем яблоко, а яблоко тяжелее персика. Что тяжелее груша или персик?
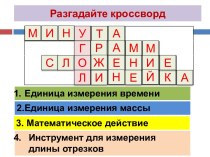
- 20. Расшифруйте слова и назовите лишнее: д и
- 21. В каком случае графикидвух линейных функций являются параллельными прямыми?
- 22. График некоторой линейной функции вида y= kx+1 параллелен графику функции y=-0,4x. Найдите значение k
- 23. Что называют графиком функции?
- 24. Какую функциюназывают прямой пропорциональностью?
- 25. Как найти координаты точки пересечения двух прямых?
- 26. В каком случае графики двух линейных функций перпендикулярны?
- 27. Найдите закономерностьи закончите числовой ряд: 0, 3, 8, 15, ?
- 28. Какую функцию называют линейной?
- 29. Что называют аргументом функции?
- 30. В каком случае графики двух линейных функций пересекаются?
- 31. График линейной функции -прямая, параллельная оси абсцисс
- 32. При использовании дидактических игр очень важно следить
- 33. Математическая сторона содержания игры всегда должна отчётливо
- 34. Преобразуйте линейное уравнение с двумя переменными 2х-5у+7=0 к виду линейной функции у=кх+m ЗЭГА
- 35. Найдите наибольшее значение линейной функции у=2х-1 на отрезке [-2;0]
- 36. Систематическое использование дидактических игр на разных этапах
- 37. • Что на Руси раньше называли " ломаными числами ?"
- 38. Ломаными числами Называли дроби.
- 39. Анализируя свой опыт можно прийти к выводу,
- 40. Скачать презентацию
- 41. Похожие презентации
“Истинный педагог постарается сделать учение занимательным, но никогда не лишит его характера серьезного труда, требующего усилия воли”К.Д. Ушинский


































![Использование дидактических игр на уроках математики Найдите наибольшее значение линейной функции у=2х-1 на отрезке [-2;0]](/img/tmb/7/649586/3baff69a8bf135f0f9c1c94fc8476e8f-720x.jpg)





Слайд 2 “Истинный педагог постарается сделать учение занимательным, но никогда
не лишит его характера серьезного труда, требующего усилия воли”
УшинскийСлайд 3 Возникновение интереса к математике у большинства учащихся зависит
в большей степени от методики её преподавания, от того,
насколько умело будет построена учебная работа. Надо позаботиться о том, чтобы на уроках математики каждый ученик работал активно и увлечённо, и использовать это как отправную точку для возникновения и развитиялюбознательности, глубокого
познавательного интереса.
Слайд 4 Немаловажная роль здесь отводится дидактическим играм на уроках
математики — современному
и признанному методу обучения и воспитания,
обладающему образовательной, развивающей и воспитывающей функциями, которые действуют в
органическом единстве.
Слайд 5 На своих уроках учитель всегда
использует
возможность заинтересовать учащихся
материалом. Это и дидактические карточки
со сказочным сюжетом, плакаты, использование ТСО. В современных условиях, когда в каждой школе имеются интерактивные доски, мультимедийные установки, задача для учителя стала более реалистичной. Создание презентаций, дидактических игр стало интересным процессом, который приносит радость не только создателю, но и ученику, для которого всё это создаётся.
Слайд 6
Игра – творчество, игра – труд. В процессе
игры у детей вырабатывается привычка сосредоточиться, мыслить самостоятельно, развивается
внимание, стремление к знаниям. Увлёкшись, дети не замечают, что учатся: познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию.Слайд 7 Даже самые пассивные из детей включаются в игру
с огромным желанием, прилагая все усилия, чтобы не подвести
товарищей по игре. Во время игры дети, как правило, очень внимательны, сосредоточенны и дисциплинированны. Дидактические игры очень хорошо уживаются с «серьезным» учением.Включение в урок дидактических игр и игровых моментов делает процесс обучения интересным и занимательным.
Слайд 8 Предмет математики настолько серьезен, что полезно не упускать возможности
сделать
его немного более занимательным.
Б.Паскаль
Слайд 9 На своих уроках математики использую задания, большинство которых
имеют занимательную форму. Обычные примеры, задачи принимают форму игры,
которую интересно пройти до конца. Выполнение такого рода заданий позволяет расширить кругозор учащихся в историческом аспекте, пополнить лексический запас новыми терминами, получить дополнительную информацию об окружающем мире.Слайд 10 Например, при изучении темы «Сложение и вычитание десятичных
дробей» в 6 классе можно использовать «Математическое лото» на
интерактивной доске, где при решении примеров, открывается картинка. Неправильно выполненное задание не открывается, а верное – открывает часть картинки.Слайд 13 Такого рода задания создают в классе атмосферу соревнования.
Кто быстрее, кто правильнее выполнит задание. Или, расставить числа
в порядке убывания (возрастания). При верном выполнении задания, складывается картинка, которуюможно угадать, расссказать о ней, и т.д.
Слайд 16 Занимательная форма многих заданий привлекает учащихся, побуждает их
к чёткой, последовательной и аккуратной деятельности. В 7 –
9 классах на уроках алгебры многие понятия учащиеся узнали из заданий.Слайд 17 Выполните преобразования. Используя найденные ответы, запишите в таблицах
два высказывания Козьмы Прудкова будь х5
· х2 = плачем х12 : х = быть х3 · х = имеем х8 : х2 = что х2· х3· х4 = потерявши х· х2· х3 : х6= не х4· х5· х = храним х3· х4· х5 : х7 = им х10 : х8 = счастливым хочешь х7 : х6 =
Слайд 22
График некоторой
линейной функции
вида y= kx+1
параллелен
графику
функции y=-0,4x.
Найдите значение k
Слайд 31
График линейной функции -
прямая, параллельная
оси абсцисс и
проходящая
через точку M(5;8).
Задайте эту функцию
формулой
Слайд 32 При использовании дидактических игр очень важно следить за
сохранением интереса школьников к игре.
При отсутствии интереса или
угасания его ни в коем случае не следует принудительно навязывать игру детям, так как игра по обязанности теряет своё дидактическое, развивающее значение; в этом случае из игровой деятельности выпадает самое ценное – её эмоциональное начало.Слайд 33 Математическая сторона содержания игры всегда должна отчётливо выдвигаться
на первый план. Только тогда игра будет выполнять свою
роль в математическом развитии детей и воспитании интереса их к математике.Создание игровых ситуаций на уроках математики повышает интерес к математике, вносит разнообразие и эмоциональную окраску в учебную работу, снимает утомление, развивает внимание, сообразительность, чувство соревнования, взаимопомощь.
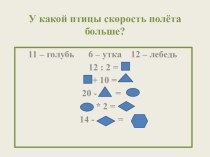
В 7 классе использую математические ребусы, где в результате правильного решение получаем фамилию выдающегося математика.
Слайд 34 Преобразуйте линейное уравнение с двумя переменными 2х-5у+7=0 к
виду линейной функции у=кх+m
З
Э
Г
А
Слайд 36 Систематическое использование дидактических игр на разных этапах изучения
различного по характеру математического материала является эффективным средством активизации
учебной деятельности школьников, положительно влияющим на повышение качества знаний, умений и навыков учащихся, развитие умственной деятельности.Слайд 39 Анализируя свой опыт можно прийти к выводу, что
применение дидактических игр и упражнений в игровой форме на
уроках математики дает рост интереса к предмету, созданию положительную эмоциональную обстановку, развивают логическое и аналитическое мышление. Так, дети, хорошо успевающие, в большей степени смогли развернуть свои мыслительные способности в условиях решения нестандартных задач, требующих сообразительности и находчивости.А дети слабоуспевающие, решая нестандартные задачи, но относительно легкие, посильные для них, смогли обрести уверенность в своих силах, научиться управлять своими поисковыми действиями, подчинять их определенному плану.