Презентация на тему Объем шара и площадь сферы

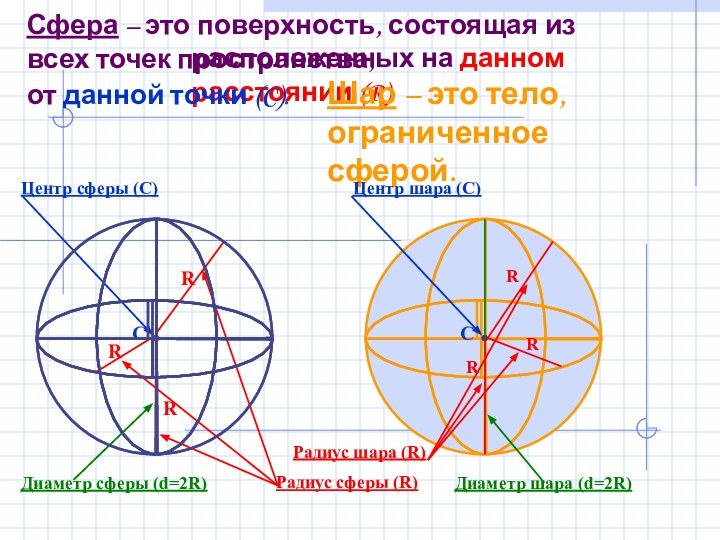
пространства,
расположенных на данном расстоянии (R)
от данной точки (C).
Центр

Радиус сферы (R)

Диаметр сферы (d=2R)

Шар – это тело, ограниченное сферой.

Центр шара (С)

Радиус шара (R)

Диаметр шара (d=2R)

сегмент – это часть шара, отсекаемая от него какой-нибудь

Шаровой слой – это часть шара, заключённая между двумя параллельными секущими плоскостями.

Vш. Сегмента = Пh2(R- 1/3h)

Vш. слоя=Vш.сег.1-Vш.сег.2

Основание сегмента

Высота сегмента (h)

тело, полученное вращением кругового сектора, с углом, меньшим 90о,

вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.

Шаровой сектор состоит из шарового сегмента

и конуса.

объем этого шара, деленный на
.
Решение. Радиус вписанного в

Тогда объем шара

.
Ответ: 4,5.

ЕГЭ: В11

радиус увеличить в три раза?

Решение. Объем шара радиуса  

При увеличении радиуса втрое, объем шара увеличится в 27 раз.

Ответ: 27.

В11

шара, площадь поверхности которого равна сумме площадей их поверхностей.

Решение. Из условия

найдем, что радиус такого шара

Ответ: 10.

В11

этого шара, деленный на
Решение. Радиус описанного шара равен половине

.
Поэтому объем шара равен

Тогда

Ответ: 4,5.

В11

поверхности шара.
Решение. Радиус большого круга является радиусом шара. Площадь

как

, а площадь поверхности сферы – как 4ПR2. Видно, что площадь поверхности шара в

раза больше площади поверхности большого круга.

Ответ: 12.

В11

радиус шара увеличить в 2 раза?
Решение. Площадь поверхности шара выражается

как

, поэтому при увеличении радиуса вдвое площадь увеличится в

Ответ: 4.

раза.

В11

поверхности, деленную на
Решение. Объем шара радиуса
, откуда


Площадь

Ответ: 144.

В11

18. Найдите площадь поверхности шара.
Решение. По построению радиусы шара и

равна

Площадь поверхности шара радиусом

равна

, то есть в 1,5 раза меньше первой. Площадь поверхности шара тогда равна 12.
Ответ: 12.

В11