пропорциональность частей чего-нибудь, расположенных по обе стороны от середины,
центра».«Словарь иностранных слов»: «Симметрия – полное зеркальное соответствие в расположении частей целого относительно средней линии, центра; соразмерность».
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
















•
•
А
А1
а
а
а - ось симметрии
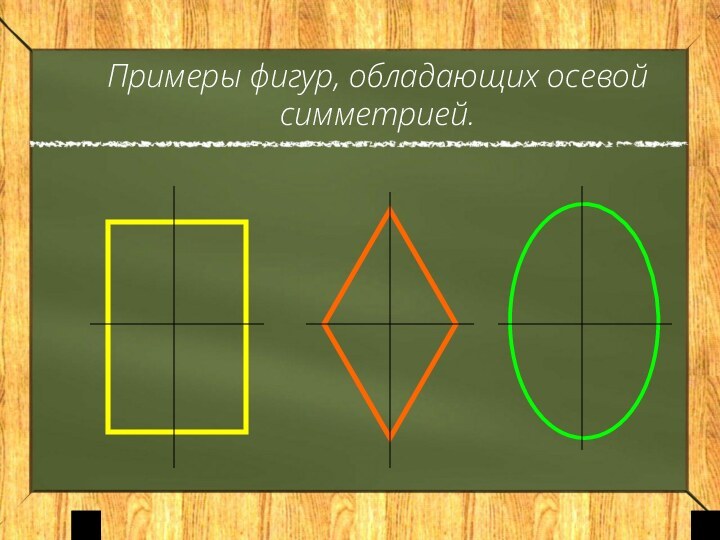
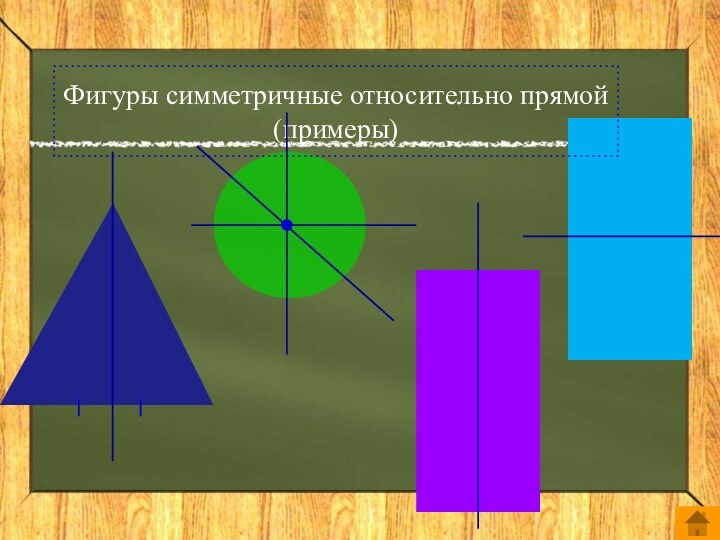
Осевая симметрия
•
•
А
А1
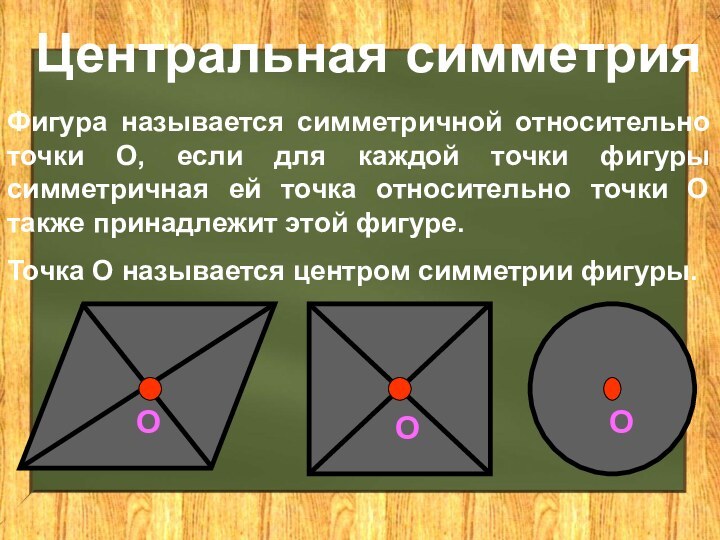
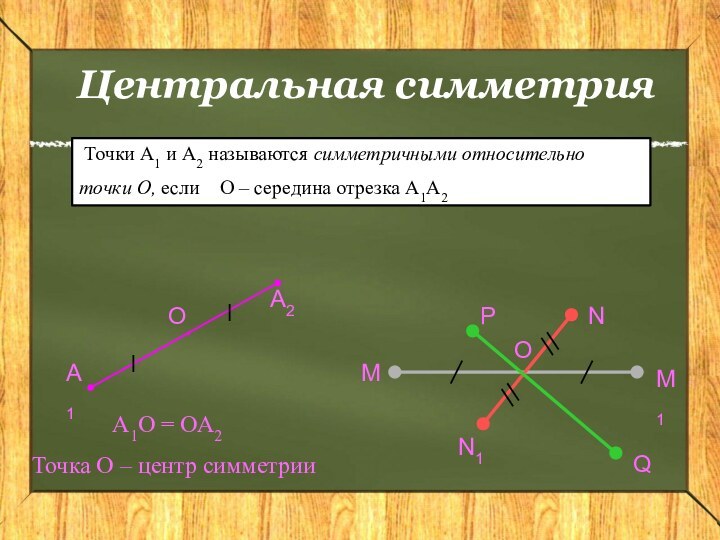
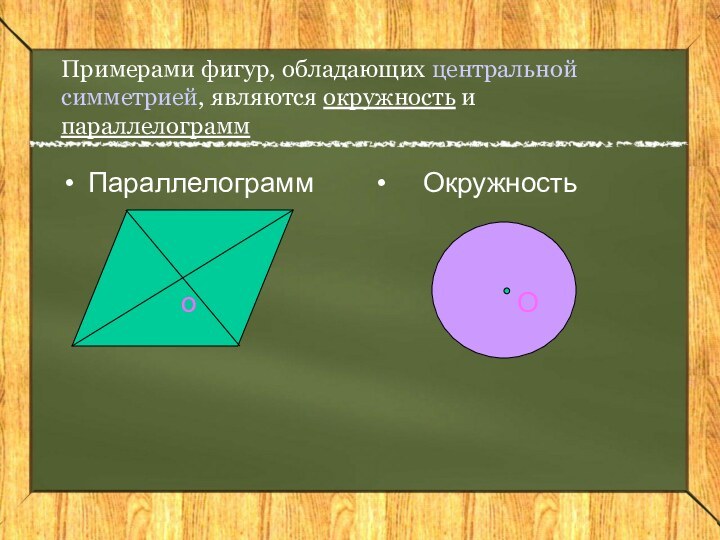
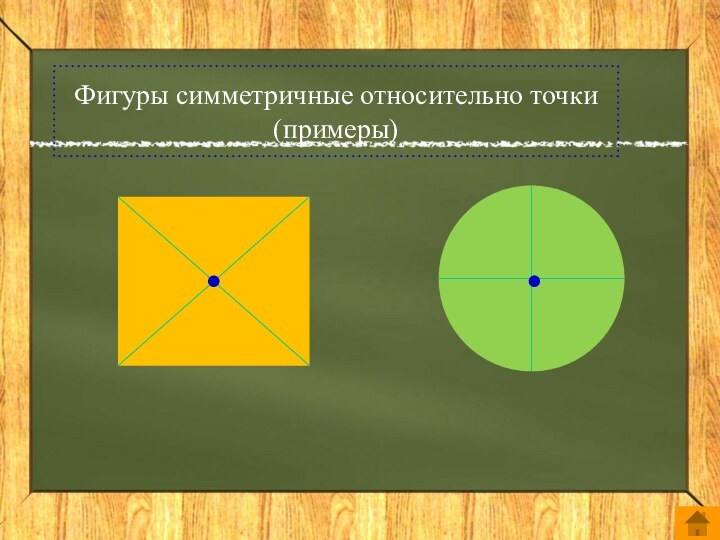
Центральная симметрия
О
О
О
А1
А2
О
О
Р
Q
M
M1
N
N1
А1О = ОА2
Точка О – центр симметрии
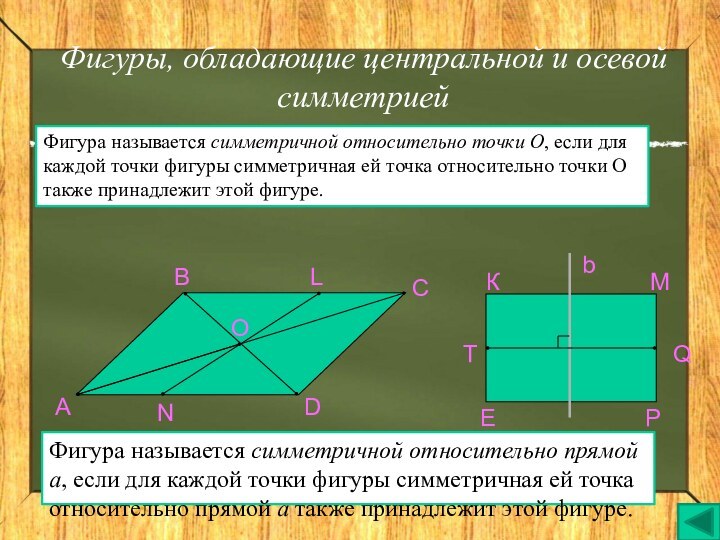
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
К
М
E
P
b
T
Q