- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задания по арифметической прогрессии
Содержание
- 2. Изучена данная
- 3. Цели урока:Обобщить теоретические знания по теме;
- 4. Хочу Могу Умею
- 5. Умение применять формулы …Умение грамотно говорить …Умение
- 6. Определение
- 7. Устная работа:3; 6; 9; 12; …-1;
- 8. Выразите через а
- 9. Задача. Родители ко Дню рождения
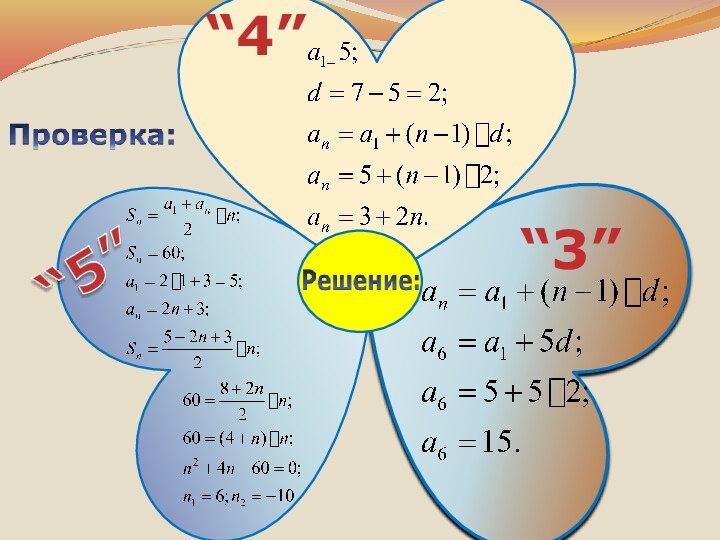
- 10. Дано: Найти: Решение:Ответ:
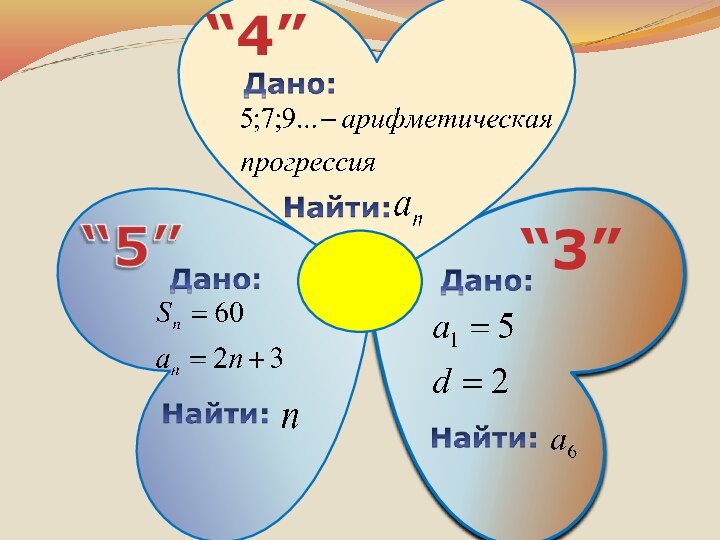
- 11. “4”“3”
- 12. “4”“3”
- 13. Задача.Для участия в международнойматематической игре «Кенгуру –
- 14. Пятый член арифметической прогрессии на 15
- 15. Вычислите сумму: 502 – 492 + 482
- 16. Свойства арифметической прогрессии Дано: (а n
- 17. Занимательное свойство арифметической прогрессии.А теперь, рассмотрим еще
- 18. Знаете ли вы, что такое магический квадрат?
- 19. Нетрудно видеть, что получился
- 20. Задания из сборника предназначенного для подготовки к
- 21. Ответы:6.1 (20,4) 6.2. (является), 6.5. (6;8,2;10’4;12’6;14’8;17.),
- 22. Урок сегодня завершён,Дружней вас не сыскать. Но
- 23. Рефлексия.Тест.Результатом своей личной работы считаю, что я
- 24. Скачать презентацию
- 25. Похожие презентации





















Слайд 3
Цели урока:
Обобщить теоретические знания по теме;
совершенствовать навыки нахождения п-го члена и суммы п первых
членов арифметической прогрессии с помощью формул; расширить знания о свойствах арифметической прогрессии и применять их при решении задач;Видеть связь между математикой и окружающей жизнью;
развивать грамотную математическую речь;
Воспитывать волю и настойчивость для достижения конечных результатов.
Слайд 5
Умение применять формулы …
Умение грамотно говорить …
Умение обобщать,
систематизировать …
Умение логически мыслить …
Умение пересказывать …
Умение молчать …
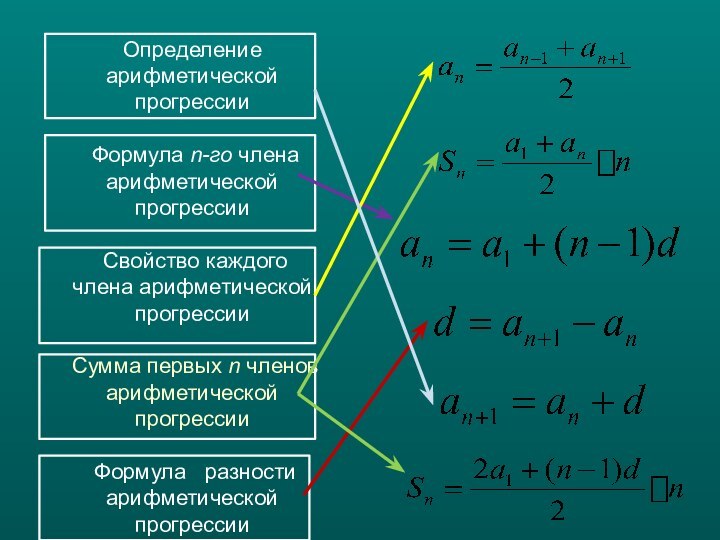
Слайд 6 Определение
арифметической прогрессии Формула n-го члена арифметической прогрессии Свойство каждого члена арифметической прогрессии Сумма первых n членов арифметической прогрессии Формула разности арифметической прогрессии
Слайд 7
Устная работа:
3; 6; 9; 12; …
-1; -1;
-1; …
0; 13; 1; 14; …
= 3п –
2;= 25 + ;
-3; -1; 1; 3; …
Является ли заданная последовательность арифметической прогрессией, почему?
Слайд 8
Выразите через а
и d а , а
, аНайдите а , если а = 4, d =7.
Найдите а , если а = 20, а = 30.
1
8
33
100
5
1
12
11
13
Слайд 9
Задача.
Родители ко Дню рождения
своего сына Андрея решили купить и обновить ему мобильный
телефон. Для этого они в первый месяц отложили 650 рублей, а в каждый последующий месяц они откладывали на 50 рублей больше, чем в предыдущий. Какая сумма будет у родителей Андрея через 10 месяцев?…
Слайд 13
Задача.
Для участия в международной
математической игре
«Кенгуру – математика
для всех»
в региональный оргкомитет
необходимо подать заявку от школы.
Впервый день после указанного срока заявки на участие подали 5 школ, во второй -7, в третий - 9 … Через сколько дней в оргкомитет будет подано 60 заявок (считая, что полученная закономерность не будет нарушена)? Сколько заявок поступит в последний день?
Слайд 14 Пятый член арифметической прогрессии на 15 меньше
второго. Сумма третьего и седьмого её членов равна -6.
Найдите третий и четвёртый члены этой прогрессии. Составьте систему уравнений и воспользуйтесь формулой n-го члена арифметической прогрессии:
а2-а5=15,
а3+а7=-6;
а1+ d - (а1+ 4d)=15,
(а1+2d) + (а1+6d) =-6;
d=-5,
а1=17;
а3=а1+2d, а3=7,
а4=а3+d, а4=2.
Ответ: а3=7, а4=2.
Слайд 15
Вычислите сумму:
502 – 492 + 482 –
472 + 462 – 452 +…
… + 42 – 32 +22 – 12;1) Воспользуйтесь формулой разности квадратов:
(50-49)(50+49) + (48-47)(48+47) + (46-45)(46+45) +…
…+ (4-3)(4+3) + (2-1)(2+1);
2) Выполните действия в скобках:
99 + 95 + 91 + 87 +… + 7 + 3; эти числа образуют убывающую арифметическую прогрессию a1=99, an=3, n=25.
Ответ: сумма равна 1275.
Слайд 16
Свойства
арифметической прогрессии
Дано: (а n ) арифметическая
прогрессия
а4=12,5; а6=17,5
Найти: а5
Решение:
используя свойство арифметической прогрессии имеем:
Ответ:15
Решeние
Слайд 17
Занимательное свойство арифметической прогрессии.
А теперь, рассмотрим еще одно
свойство членов арифметической прогрессии. Оно, скорее всего, занимательное. Нам
дана “стайка девяти чисел”3, 5, 7, 9, 11, 13, 15,17, 19.
Она представляет собой арифметическую прогрессию. Кроме того, данная стайка чисел привлекательна способностью разместиться в девяти клетках квадрата так, что образуется магический квадрат с константой, равной 33
Слайд 18
Знаете ли вы, что такое магический квадрат?
Квадрат, состоящий из 9 клеток, в него вписывают
числа, так чтобы сумма чисел по вертикали, горизонтали диагонали была одним и тем же числом – constanta. Замечание об арифметической прогрессии само по себе очень интересно. Дело в том, что из каждых девяти последовательных членов любой арифметической прогрессии натуральных чисел можно составить магический квадрат.
Слайд 19
Нетрудно видеть, что
получился магический
квадрат, константа C
которого равна 3a+12d.
Действительно, суммачисел в каждой строке,
в каждом столбце и по каждой диагонали квадрата равна 3a+12d.
Пусть дана арифметическая прогрессия: a, a+d, a+2d, a+3d, …, a+8d, где a и d натуральные числа. Расположим её члены в таблицу.
Слайд 20 Задания из сборника предназначенного для подготовки к итоговой
аттестации в новой форме по алгебре в 9 классе,
предлагаются задания которые оцениваются в 2 балла:6.1. 1) Пятый член арифметической прогрессии равен 8,4, а ее десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии.
6.2. 1) Число –3,8 является восьмым членом арифметической прогрессии (ап), а число –11 является ее двенадцатым членом. Является ли членом этой прогрессии число –30,8?
6.5. 1) Между числами 6 и 17 вставьте четыре числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию.
Слайд 22
Урок сегодня завершён,
Дружней вас не сыскать.
Но каждый
должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут.
Слайд 23
Рефлексия.
Тест.
Результатом своей личной работы считаю, что я ..
А.
Разобрался в теории.
В. Научился решать задачи.
С. Повторил весь ранее
изученный материал.Что вам не хватало на уроке при решении задач?
А. Знаний. Б. Времени. С. Желания.
Д. Решал нормально.
Кто оказывал вам помощь в преодолении трудностей на уроке?
А. Одноклассники. Б. Учитель.
С. Учебник. Д. Никто.