- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Парная линейная регрессия. Оценивание по МНК коэффициентов регрессии
Содержание
- 2. ПланМетод наименьших квадратов (МНК).Перечень средств MS Excel.Алгоритм применения функции ЛИНЕЙН.Результаты оценивания регрессии.
- 3. Цели обучениянаучиться применять МНК для оценивания теоретических
- 4. Метод наименьших квадратов (МНК)Пусть в генеральной совокупности
- 5. Цель МНК – выполнить наилучшую ”подгонку” прямой
- 6. Суть МНК:следует найти такие коэффициенты уравнения регрессии,
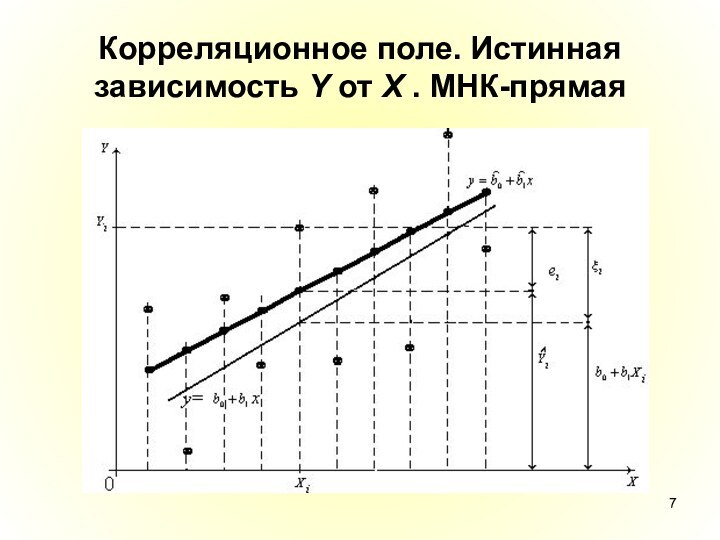
- 7. Корреляционное поле. Истинная зависимость Y от X . МНК-прямая
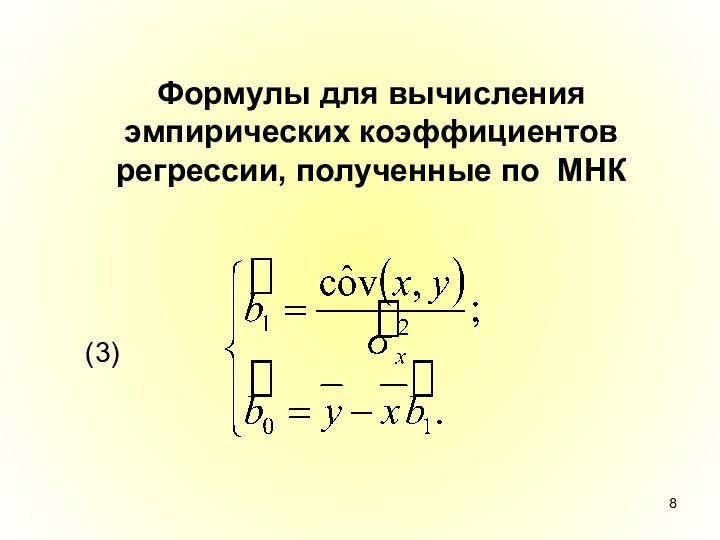
- 8. Формулы для вычисления эмпирических коэффициентов регрессии, полученные
- 9. Пример 1. Есть данные о
- 10. Перечень средств MS ExcelВстроенная статистическая функция MS
- 11. Краткие сведенияФункция СУММКВРАЗН(массив_1;массив_2) вычисляет сумму квадратов разностей
- 12. Алгоритм применения функции ЛИНЕЙНЗанести в ячейки с
- 13. Алгоритм применения функции ЛИНЕЙН (продолжение)Задать значения четырех
- 14. Результаты применения функции ЛИНЕЙНВ левой из двух
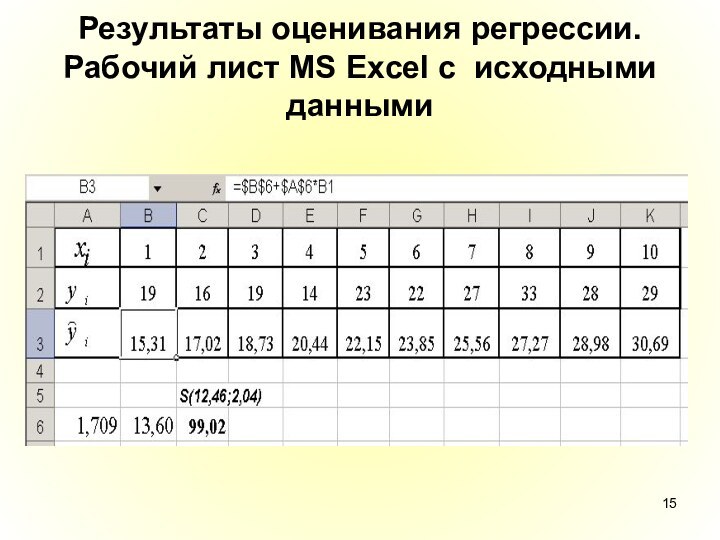
- 15. Результаты оценивания регрессии. Рабочий лист MS Excel c исходными данными
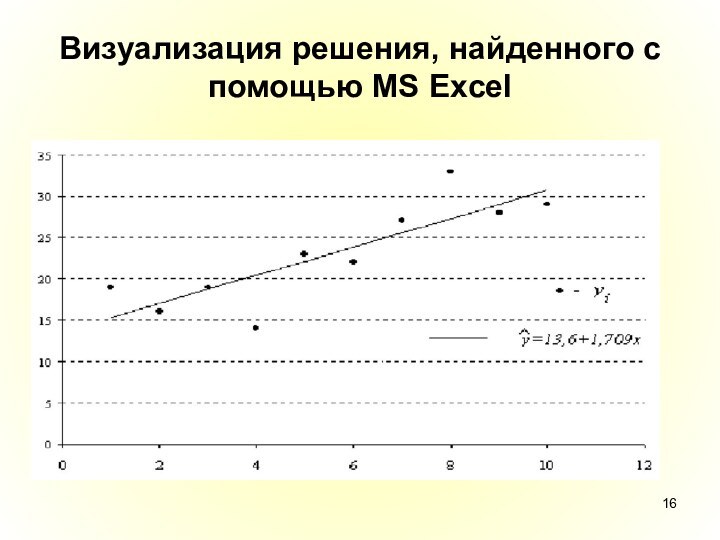
- 16. Визуализация решения, найденного с помощью MS Excel
- 17. Основные варианты задания логических аргументов функции ЛИНЕЙН
- 18. Варианты вывода результатов функции ЛИНЕЙН для случая
- 19. Скачать презентацию
- 20. Похожие презентации
ПланМетод наименьших квадратов (МНК).Перечень средств MS Excel.Алгоритм применения функции ЛИНЕЙН.Результаты оценивания регрессии.














Слайд 2
План
Метод наименьших квадратов (МНК).
Перечень средств MS Excel.
Алгоритм применения
функции ЛИНЕЙН.
Слайд 3
Цели обучения
научиться применять МНК для оценивания теоретических коэффициентов
уравнения парной линейной регрессии;
изучить структуру дополнительной регрессионной статистики функции
ЛИНЕЙН табличного процессора MS Excel.
Слайд 4
Метод наименьших квадратов (МНК)
Пусть в генеральной совокупности зависимость
между переменными Y и X имеет вид:
(1)Типичный вид корреляционного поля данных наблюдений для выборки значений (Xi,Y i), объемом n из генеральной совокупности:
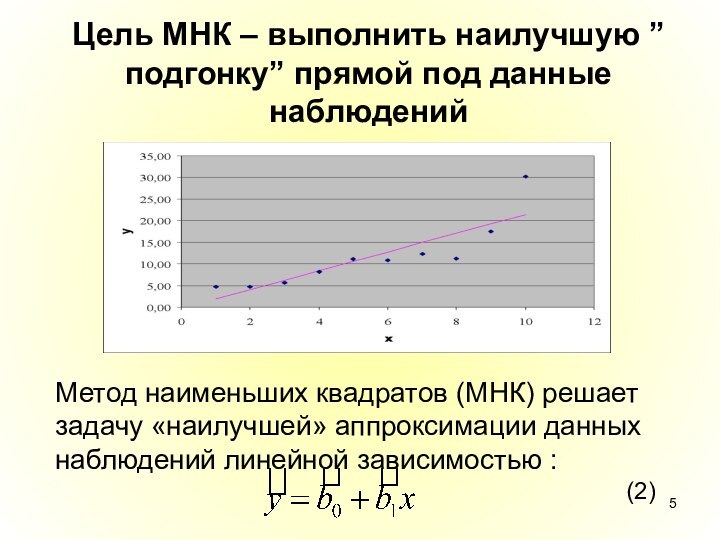
Слайд 5 Цель МНК – выполнить наилучшую ”подгонку” прямой под
данные наблюдений
Метод наименьших квадратов (МНК) решает задачу «наилучшей»
аппроксимации данных наблюдений линейной зависимостью : (2)
Слайд 6
Суть МНК:
следует найти такие коэффициенты уравнения регрессии, чтобы
сумма квадратов отклонений эмпирических значений результативного признака от расчетных,
вычисленных по уравнению, была бы минимальной, т.е.
Слайд 9 Пример 1. Есть данные о количестве внесенных удобрений
(Y, кг/га) и урожайности пшеницы (X, ц/га) по десяти
фермерским хозяйствам:Считая форму связи между признаками Y и X линейной,1) найти по МНК эмпирические коэффициенты регрессии; 2) построить корреляционное поле и эмпирическую линию регрессии; 3) вычислить значение функции
Слайд 10
Перечень средств MS Excel
Встроенная статистическая функция MS Excel
КОВАР(массив_1;массив_2).
Встроенная математическая функция MS Excel СУММКВРАЗН(массив_1;массив_2).
Встроенная статистическая функция ЛИНЕЙН
(известные_значения_y ; известные_значения_x; конст; статистика ).Мастер диаграмм.
Слайд 11
Краткие сведения
Функция СУММКВРАЗН(массив_1;массив_2) вычисляет сумму квадратов разностей между
соответствующими компонентами массивов.
Функция КОВАР(массив_1;массив_2) находит выборочную ковариацию данных наблюдений,
представленных в массивах.Функция ЛИНЕЙН (известные_значения_y ; известные_значения_x; конст; статистика ) находит по МНК оценки коэффициентов регрессии и дополнительную регрессионную статистику.
Точечная диаграмма позволяет визуализировать точки из двумерной совокупности.
Слайд 12
Алгоритм применения функции ЛИНЕЙН
Занести в ячейки с адресами
B1:K1 рабочего листа MS Excel значения X, а в
ячейки B2:K2 – значения Y.Выделить интервал из двух ячеек A6:B6 . Вставка -> Функция.
Выбрать категорию (вид функции) – «Статистические». Затем в списке с названиями статистических функций, упорядоченными по алфавиту, найти функцию ЛИНЕЙН.
ЛИНЕЙН -> ОК.
Слайд 13
Алгоритм применения функции ЛИНЕЙН (продолжение)
Задать значения четырех аргументов
функции ЛИНЕЙН.
Первый аргумент: известные_значения_y -> B2:K2.
Второй аргумент: известные_значения_x -> B1:K1.Задать значения необязательных логических аргументов конст и статистика по умолчанию, т.е.: конст ->1; статистика -> 0.
7. ОК.
Слайд 14
Результаты применения функции ЛИНЕЙН
В левой из двух выделенных
ячеек (A6) появится первый элемент итоговой таблицы – величина
коэффициента .Для того, чтобы получить всю таблицу, следует сначала нажать клавишу F2, а затем –комбинацию клавиш: CTRL+SHIFT+ENTER.
В ячейке B6 появится значение коэффициента .
Слайд 18 Варианты вывода результатов функции ЛИНЕЙН для случая парной
линейной регрессии
сокращенный
[конст =1 (или истина),
статистика = 0
(или ложь)]
полный
[конст =1 (или истина),
статистика =1
(или истина)]