Презентация на тему Показательные уравнения. Подготовка к ЕГЭ

трудом даётся
Цель:
Повторить и обобщить материал по теме

«Показательные уравнения»;
Решение показательных уравнений различных видов;
Подготовка к ЕГЭ.

х∙у, где (х;∙у) – решение системы:

5х (у

– 0,2) = − 1,
5х – у = 5.

ЕГЭ – 2008
В1 Решить уравнения:
а) х∙63х − 36∙63х = 0
б) 4 х +1 + 8∙4х = 3

ЕГЭ - 2009
В4 Найдите
х + у, где:
х – у = 1,
64х – 56∙8у = 8.

ЕГЭ - 2010
В3 7х – 2 = 49.

С1 Решите уравнение:

4 х2+3х–2 − 0,5 2х2+2х–1= 0

ЕГЭ – 2010
Решите систему ур-ий:

С3 5∙5 tgy + 4 = 5 -tgy,

√х – 5 + 4сosy = 0.

о показательных ур-ий
аf(x) = ag(x) f(x) = g(x))
Метод

введения новой переменной

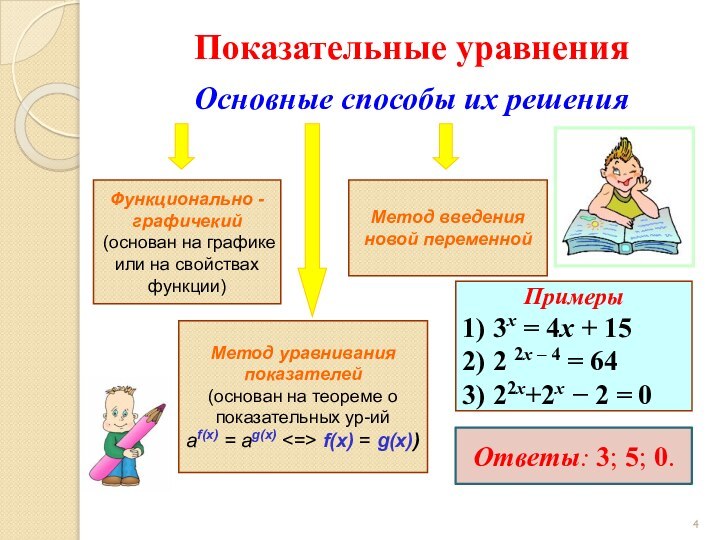
Примеры
1) 3х = 4х + 15
2) 2 2х – 4 = 64
3) 22х+2х − 2 = 0

Функционально - графичекий (основан на графике или на свойствах функции)

Показательные уравнения

Ответы: 3; 5; 0.

одинаковыми основаниями. Приём: вынос за скобку степень с наименьшим

показателем)

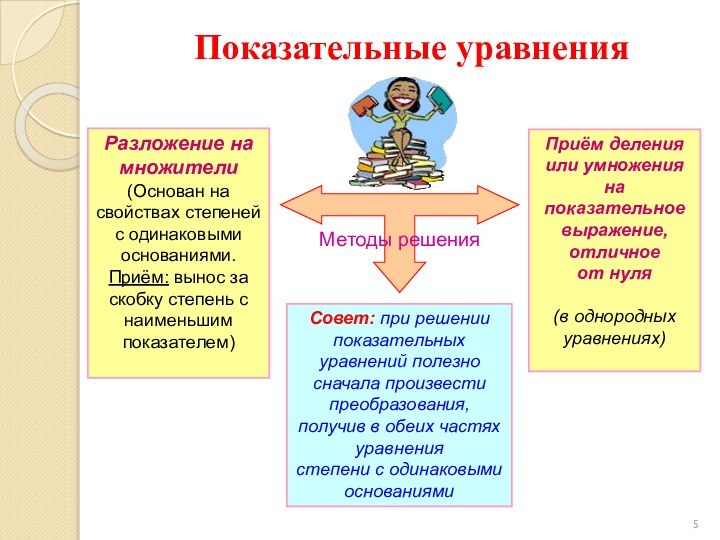
Приём деления или умножения
на показательное выражение, отличное
от нуля

(в однородных уравнениях)

Показательные уравнения

Совет: при решении показательных уравнений полезно сначала произвести преобразования, получив в обеих частях уравнения
степени с одинаковыми основаниями

Методы решения

4 х – 2 = 124,

4 х – 2 ∙ (43 − 2) = 124, 4 х – 2 ∙ 62 = 124,
4 х – 2 = 2, 4 х - 2 = 40,5,…
2 ∙ 22х − 3 ∙ 2х ∙ 5х − 5 ∙ 52х = 0│
: 52х ≠ 0,
2 ∙ (2/5)2х − 3 ∙ (2/5) х − 5 = 0,
t = (2/5) х (t > 0), 2t 2 − 3 t − 5 = 0,
t = − 1, t = 5/2 (?...).
5/2 = (2/5)х,

х = 2,5

х = −1

МОЛОДЦЫ!

б) (1/6) 12 – 7х = 36.

Ответ: а) х = 4, б) х = 2.
С1: 4 х2 + 3х – 2 − 0,5 2х2 + 2х – 1= 0. (Можно 0,5 = 4– 0,5)
Решение. 4 х2 + 3х – 2 = 4 −х2 − х + 0,5
х2 + 3х – 2 = −х2 − х + 0,5, …
Ответ: х = −5/2, х = ½.
С3: 5 ∙ 5 tgy + 4 = 5 −tgy, при сosy < 0.
Указание к решению.
5 ∙ 5 tgy + 4 = 5−tgy │∙ 5 tgy ≠ 0,
5 ∙ 5 2gy + 4 ∙ 5 tgy – 1 = 0. Пусть х = 5 tgy , …
5 tgy = − 1 (?...), 5 tgy = 1/5, tgy = − 1.
Так как tgy = − 1 и сosy < 0, то у  … к.ч.
у  II к.ч., значит,

Решение заданий ЕГЭ – 2010 года

у = 3π/4 + 2πk, k  N.

22х – 3 ∙ 2х +

а2 – 4а = 0 имеет два корня?
Решение.
Пусть t = 2х, t > 0, t 2 – 3t + (а2 – 4а) = 0 .
1) Т. к. уравнение имеет два корня, то D =…
2) Т. к. t1, 2 > 0, то t1 ∙ t2 > 0, т. е. а2 – 4а > 0 (?...).
Значит,
D > 0, −4а2 + 16а + 9 > 0,
а2 – 4а > 0; а (а − 4) > 0; …
Ответ: а  (-0,5; 0) или (4; 4,5).

D > 0.

)2

2. у = 5х – 1

у =

3. 5∙2х + 3 − 4∙2х – 1 = 19

4*. 3∙9х = 2∙15х + 5∙25х

2010 годов
выбрать задания по теме и

решить их.
Решить уравнения и систему уравнений:
1. (2 )х + 7 = 9/49

2. у = 3х + 2
у =

3. 2 ∙ 3х + 1 − 4 ∙ 3х – 1 = 42
4* 2 ∙ 4х − 3 ∙ 10х = 5 ∙ 25х