Слайд 2
Основной целью дисперсионного анализа является исследование значимости различия
между средними.
Установить различаются ли три группы или более
по какому-либо одному количественному признаку
Например определить, зависит ли активность фермента от стадии заболевания
Слайд 3
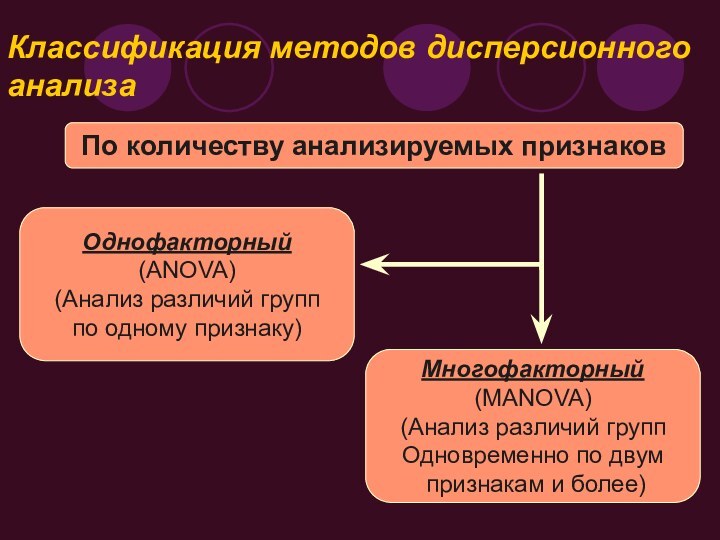
Классификация методов дисперсионного анализа
По количеству анализируемых признаков
Однофакторный
(ANOVA)
(Анализ
различий групп
по одному признаку)
Многофакторный
(МANOVA)
(Анализ различий групп
Одновременно
по двум
признакам и более)
Слайд 4
Классификация методов дисперсионного анализа
По принципам анализа
Параметрический
(Для анализа
нормально
распределенных признаков
в группах)
Непараметрический
(для анализа количественного
признака
независимо от
вида его распределения
в группах)
Слайд 5
Классификация методов дисперсионного анализа
По анализируемым данным
Данные, полученные в
несвязанных
(независимых) выборках (в частности данные
однократных наблюдении)
Данные, полученные в
связанных
(зависимых) выборках (в частности данные
повторных наблюдений)
Слайд 6
Параметрический дисперсионный анализ
Сравнить три или более группы
по количественному нормально распределенному признаку
В процедуре параметрического анализа
вариаций общая вариация данных рассматривается как сумма двух видов вариаций:
Слайд 7
Параметрический дисперсионный анализ
1. Межгрупповая вариация – вариация между
средним каждой группы и общим средним значением всей выборки
2.
Внутригрупповая вариация – вариация между каждым объектом исследования группы и средним значением соответствующей группы
Слайд 8
Параметрический дисперсионный анализ
Если межгрупповая вариация оказывается статистически
значимо больше внутригрупповой вариации , то можно полагать, что
различия между средними значениями групп существуют
NB: если анализируются две группы, ANOVA сводится к вычислению критерия Стьюдента
Слайд 9
Параметрический дисперсионный анализ
Условия применимости метода:
Анализируемый признак является
количественным
Анализируемый признак нормально распределен в каждой из групп
Дисперсии анализируемого
признака равны
Группы определяются качественным признаком (группирующий признак является качественным)
Слайд 10
Параметрический дисперсионный анализ
Этапы выполнения:
Проверка гипотез о равенстве дисперсий
Собственно
анализ вариаций
Апостериорное сравнение групп с помощью специализированных процедур,
отличных от Т-критерия
Слайд 11
Проверка гипотез о равенстве дисперсий ( тест Левена
)
Происходит проверка нулевой гипотезы
об отсутствии различий дисперсий
в группах
Если результат свидетельствует об отсутствии различия дисперсий ( р>0,05), то применение параметрического дисперсионного анализа обосновано
Если различие дисперсий имеется ( р<0,05), то применять параметрический дисперсионный анализ не следует
Слайд 12
Апостериорные сравнения групп
Если при анализе вариаций получены
статистически значимые результаты, то можно выяснить, которые же из
нескольких групп попарно отличаются друг от друга
Слайд 13
Непараметрические методы исследования независимых групп
(м-д Краскела-Уоллиса, медианный
тест)
Используется в случае необходимости сопоставить несколько групп по
одному количественному или порядковому признаку независимо от вида его распределения в группах
Слайд 14
М-д Краскела-Уоллиса – обобщение метода Манна-Уитни для
сравнения трех и более групп
Медианный тест – наиболее эффективен
в случаях если шкала измерений признака имеет искусственные границы, т.е. большое число объектов приходится на крайние значения шкалы
Слайд 15
Непараметрические методы исследования независимых групп
Условия применимости:
Анализируемый признак
должен быть количественным или порядковым
Если распределение признака не является
нормальным
Если вид распределения неизвестен (не исследовался)
Слайд 16
Сравнение нескольких зависимых групп (непараметрический метод Фридмана)
Используется
с целью сопоставления признака на разных этапах динамического исследования
Сопоставляет
не группы участников исследования, а одних и тех же участников в разные моменты времени
Слайд 17
Сравнение нескольких зависимых групп
Условия применения метода:
Анализируемые признаки
должны быть количественными
Вид распределения признака может быть любым