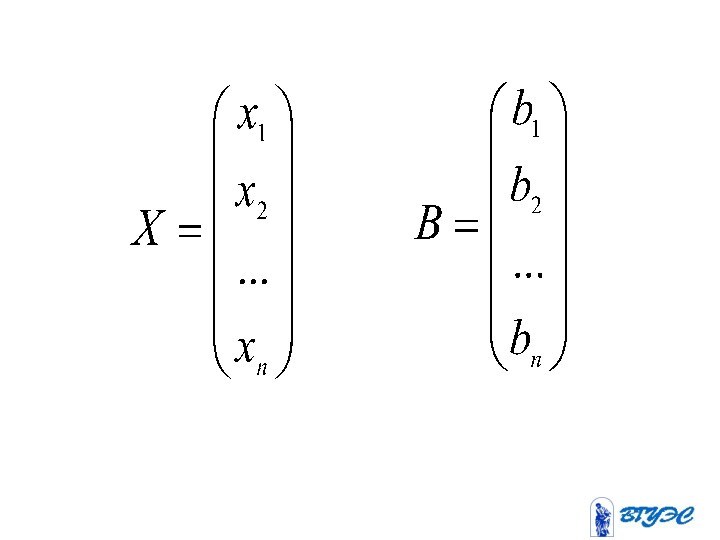
- неизвестные;
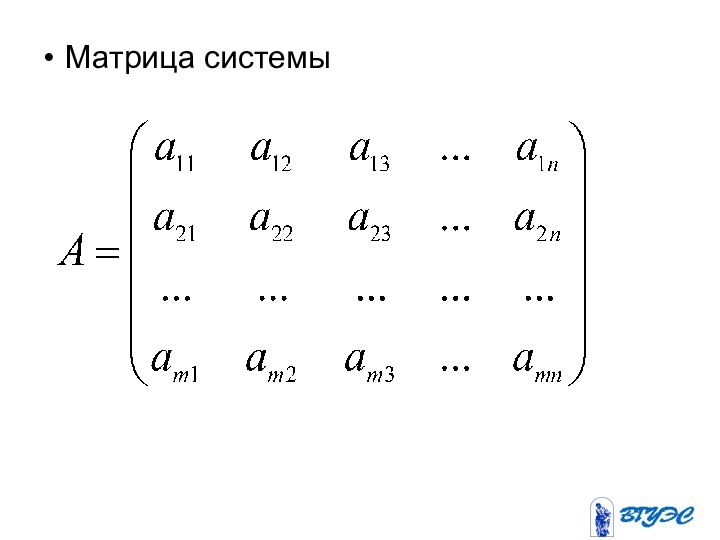
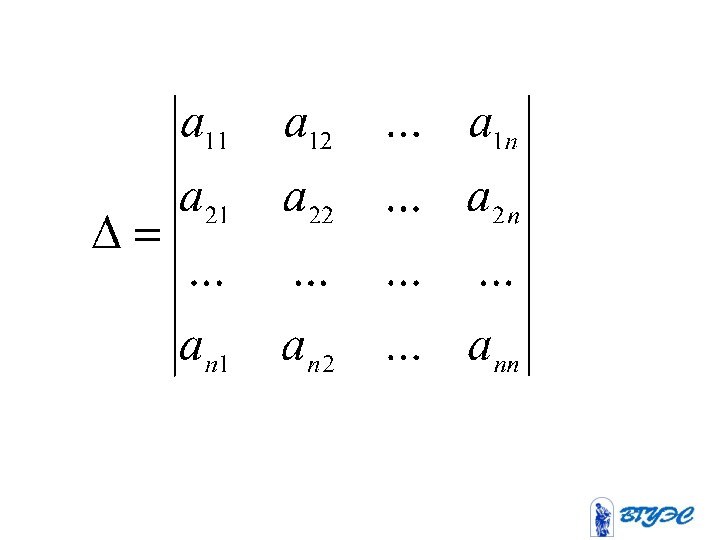
- коэффициенты при неизвестных, где - номер уравнения,
- номер неизвестного;
- свободные члены (правые части).
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

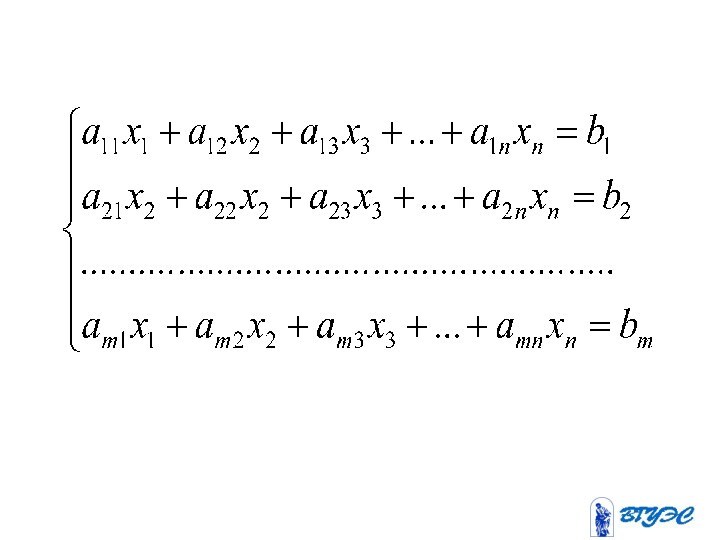















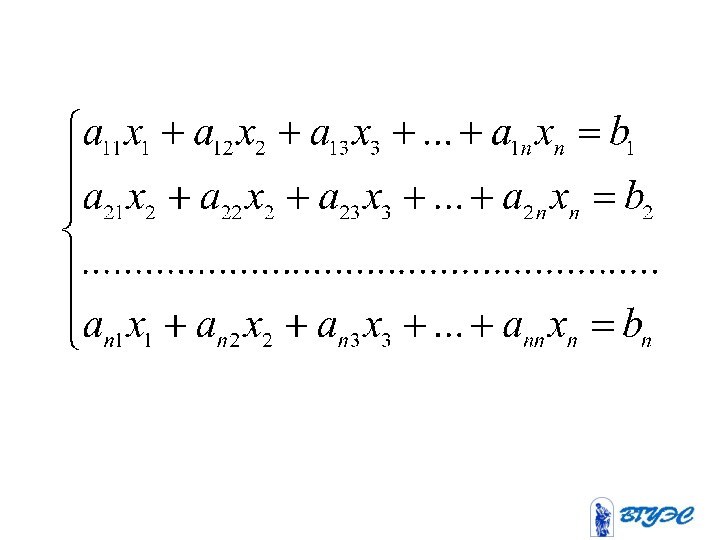
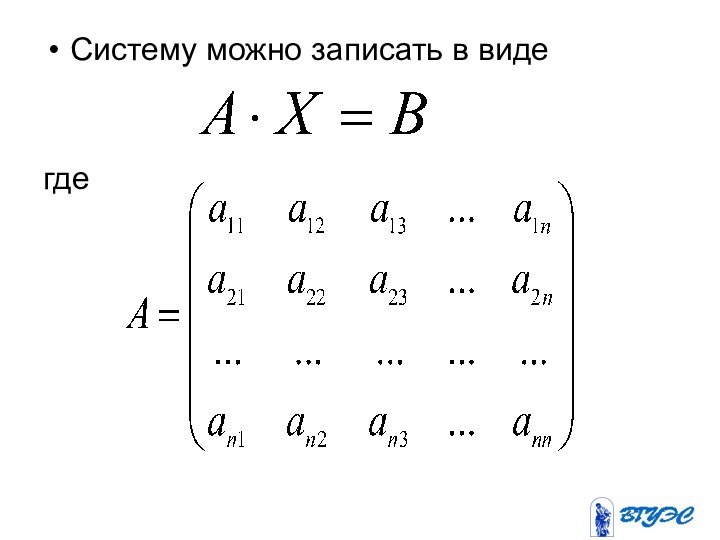



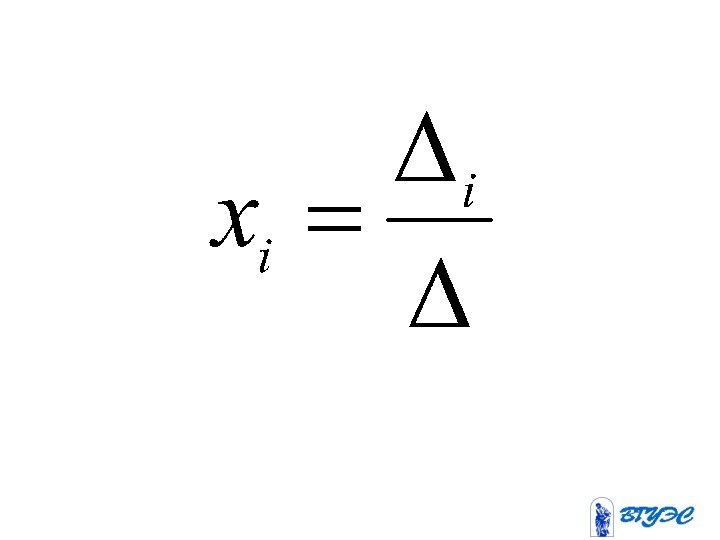

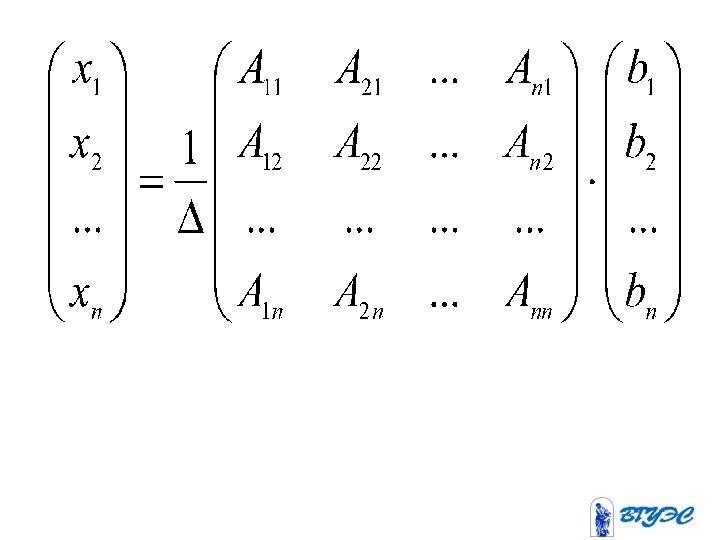






Для того чтобы система
неоднородных линейных уравнений
с неизвестными была совместной,
необходимо и достаточно, чтобы