- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Свойства и график квадратичной функции
Содержание
- 2. Цели:вспомнить свойства квадратичной функциивспомнить алгоритм построения графика квадратичной функциирассмотреть задания, предлагавшиеся на ГИА
- 3. Какая функция называется квадратичной?
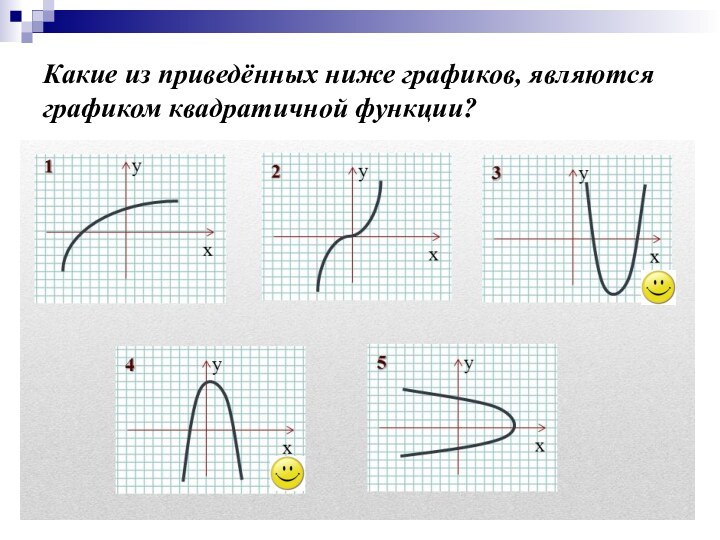
- 4. Какие из приведённых ниже графиков, являются графиком квадратичной функции?
- 5. у = 2(х-4)² +5у = -6(х-1)²у =
- 6. у= х²-6х+8y=(х²-6x +9)-1у= (х-3)²-1у= х²-4х+4у=(х-2)²(3;-1)(2;0)Найти координаты вершины параболы
- 7. УУстановите соответствие между графиком функцииформулой и координатами вершины параболы:у=-2х²+2(2; 0)
- 8. УУстановите соответствие между графиком функцииформулой и координатами вершины параболы:у = (х -3)²-3(-3;3)
- 9. ХУ11-223-1Используя правила переноса графика функции у=ах2, постройте
- 10. Как найти координаты вершины параболы для графика произвольной функции у=ах2+bх+с? Повторим формулы.уo = у(хo)
- 11. Итак:
- 12. ХУ11-223-11. D(y): R2. у=0, если х =1;
- 13. Дана функция у=ах²+bх+с. На каком рисунке изображен
- 14. На рисунке изображен график квадратичной функции. Какая
- 15. На рисунке изображен график функции у = х²+2х. Используя этот график, решите неравенство х²
- 16. На рисунке изображены графики функций вида у
- 17. На рисунке изображена парабола и три прямые.
- 18. На рисунке изображены графики функций у =
- 19. Задание на домУпражнения № 178(1), 181(1), 192(1).
- 20. Скачать презентацию
- 21. Похожие презентации
Цели:вспомнить свойства квадратичной функциивспомнить алгоритм построения графика квадратичной функциирассмотреть задания, предлагавшиеся на ГИА
Слайд 2
Цели:
вспомнить свойства квадратичной функции
вспомнить алгоритм построения графика
квадратичной функции
Слайд 5
у = 2(х-4)² +5
у = -6(х-1)²
у = -х²+12
у
= х²+4
у = (х+7)² - 9
У = 6 х²
(4;5)
(1;0)
(0;12)
(0;4)
(-7;-9)
(0;0)
Найти координаты вершины параболы
Слайд 6
у= х²-6х+8
y=(х²-6x +9)-1
у= (х-3)²-1
у= х²-4х+4
у=(х-2)²
(3;-1)
(2;0)
Найти координаты вершины параболы
Слайд 7
У
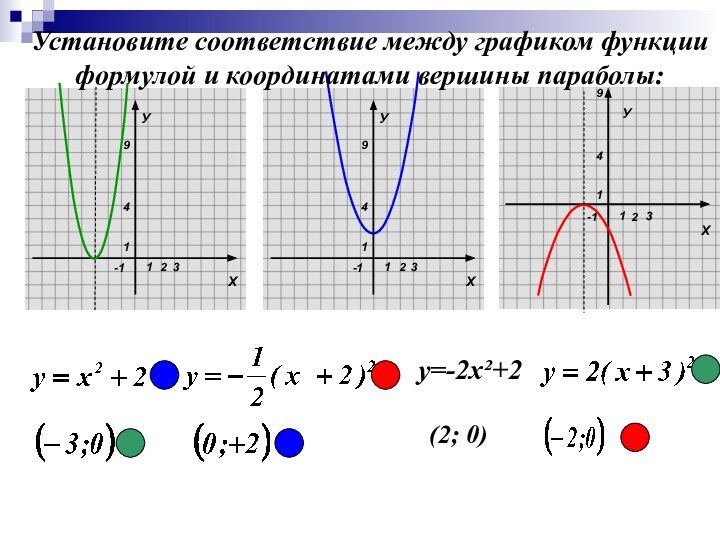
Установите соответствие между графиком функции
формулой и координатами вершины
параболы:
у=-2х²+2
(2; 0)
Слайд 8
У
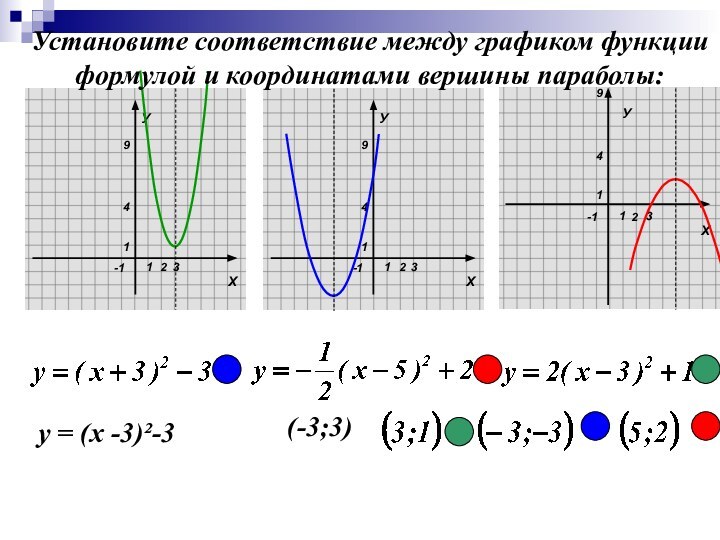
Установите соответствие между графиком функции
формулой и координатами вершины
параболы:
у = (х -3)²-3
(-3;3)
Слайд 9
Х
У
1
1
-2
2
3
-1
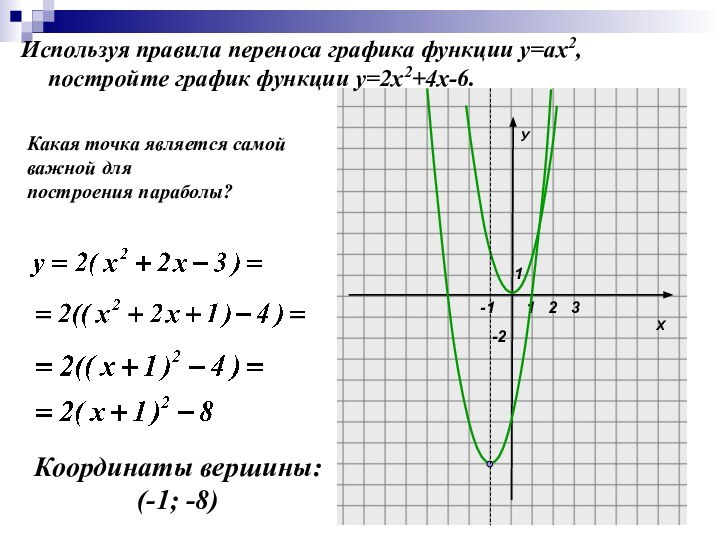
Используя правила переноса графика функции у=ах2, постройте график
функции у=2х2+4х-6.
Координаты вершины:
(-1; -8)
Какая точка является самой
важной
для построения параболы?
Слайд 10 Как найти координаты вершины параболы для графика произвольной
функции у=ах2+bх+с?
Повторим формулы.
уo = у(хo)
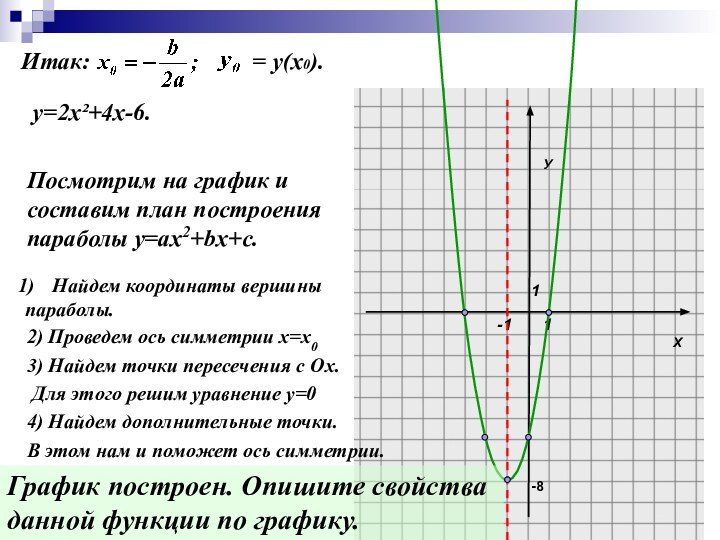
Слайд 11 Итак:
= у(х0).
Х
У
1
1
-1
Посмотрим на график и
составим план построения
параболы у=ах2+bх+с.
Найдем координаты вершины
параболы.
2) Проведем ось симметрии х=х0
3) Найдем точки пересечения с Ох.
Для этого решим уравнение у=0
4) Найдем дополнительные точки.
В этом нам и поможет ось симметрии.
График построен. Опишите свойства
данной функции по графику.
-8
у=2х²+4х-6.
Слайд 12
Х
У
1
1
-2
2
3
-1
1. D(y): R
2. у=0, если х =1; х
= -3
3. у>0, если х
4. у↓, если х
у↑, если х5. унаим= -8, если х = -1
унаиб – не существует.
6. Е(y):
Проверь себя:
у<0, если х
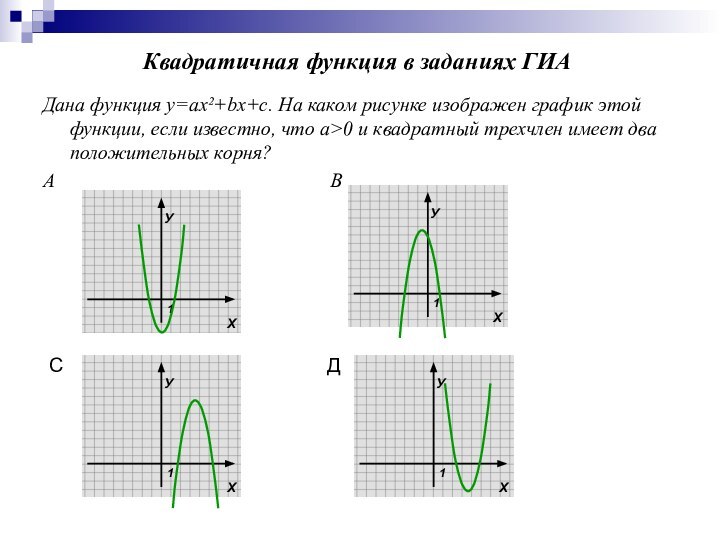
Слайд 13 Дана функция у=ах²+bх+с. На каком рисунке изображен график
этой функции, если известно, что а>0 и квадратный трехчлен
имеет два положительных корня?А В
Квадратичная функция в заданиях ГИА
С
Д
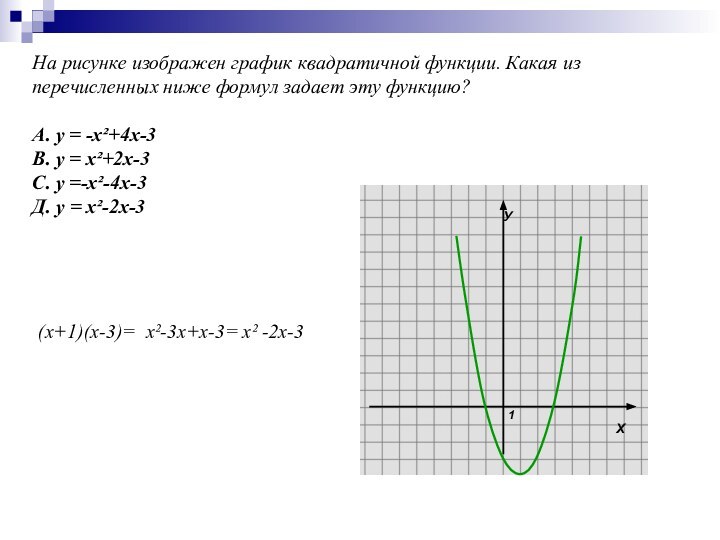
Слайд 14 На рисунке изображен график квадратичной функции. Какая из
перечисленных ниже формул задает эту функцию? А. у = -х²+4х-3 В.
у = х²+2х-3 С. у =-х²-4х-3 Д. у = х²-2х-3(х+1)(х-3)=
х²-3х+х-3=
х² -2х-3
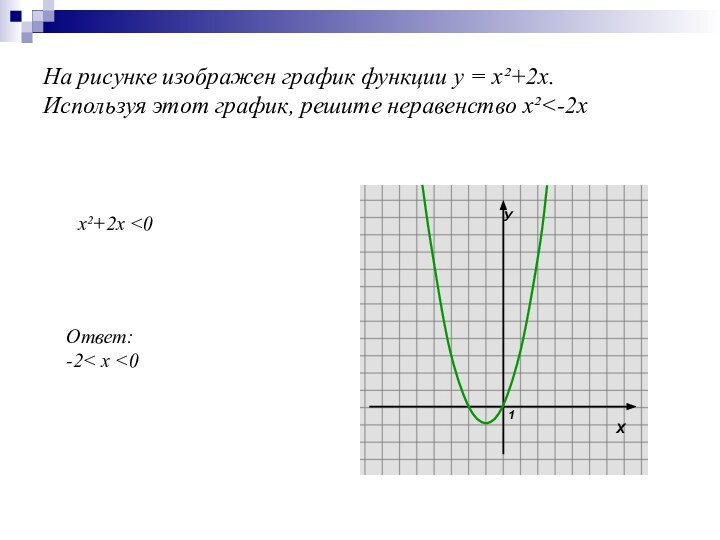
Слайд 15 На рисунке изображен график функции у = х²+2х. Используя
этот график, решите неравенство х²
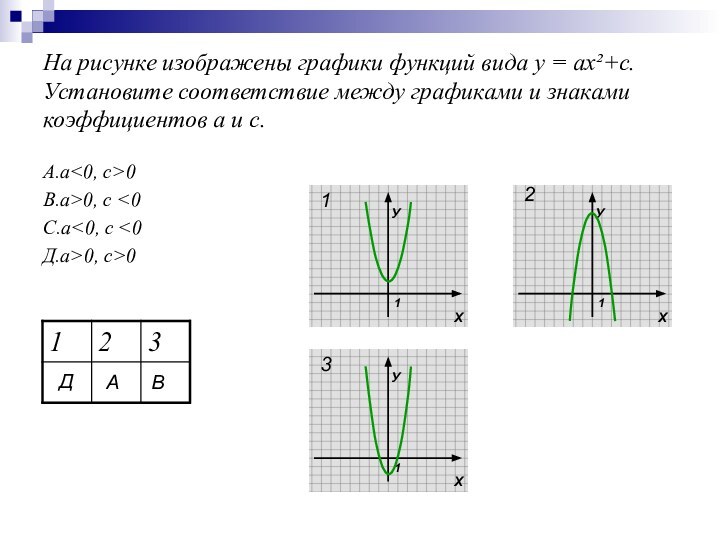
Слайд 16 На рисунке изображены графики функций вида у =
ах²+с. Установите соответствие между графиками и знаками коэффициентов а и
с.А.а<0, с>0
В.а>0, с <0
С.а<0, с <0
Д.а>0, с>0
1
2
3
Д
А
В
Слайд 17 На рисунке изображена парабола и три прямые. Укажите
систему уравнений, которая не имеет решений.
А. {
х-у=2
у = х²-1
у-10=0
х+5=0
у = х²-1
х-у=2
В.
{
у = х²-1
х+5=0
С.
{
у = х²-1
у-10=0
Д.
Все три указанные системы.
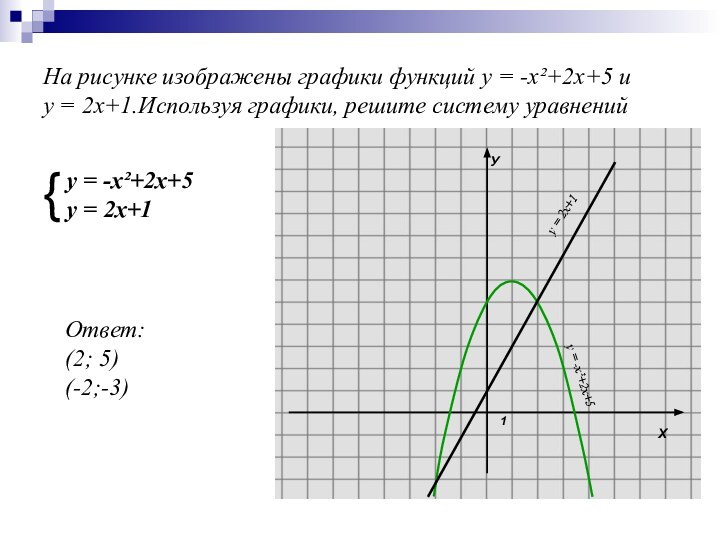
Слайд 18 На рисунке изображены графики функций у = -х²+2х+5
и
у = 2х+1.Используя графики, решите систему уравнений
{
у =
-х²+2х+5у = 2х+1
у = -х²+2х+5
у = 2х+1
Ответ:
(2; 5)
(-2;-3)
