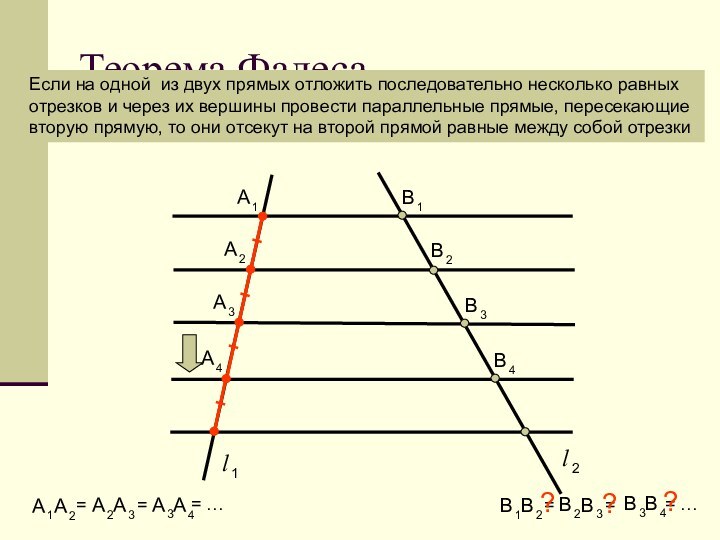
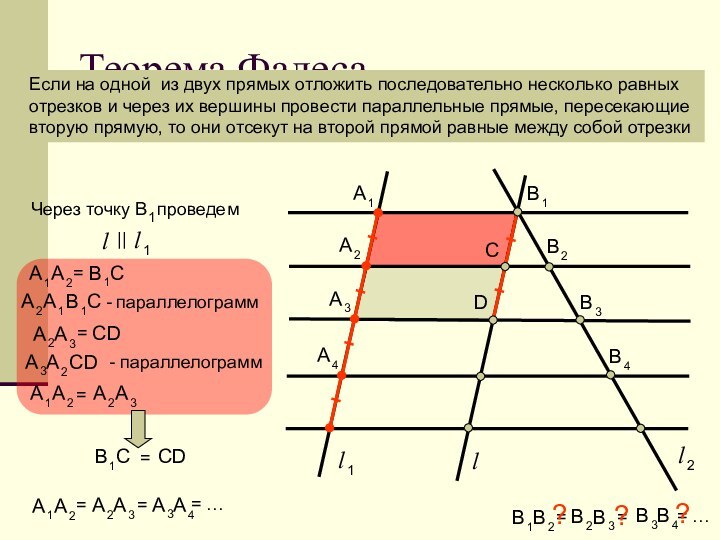
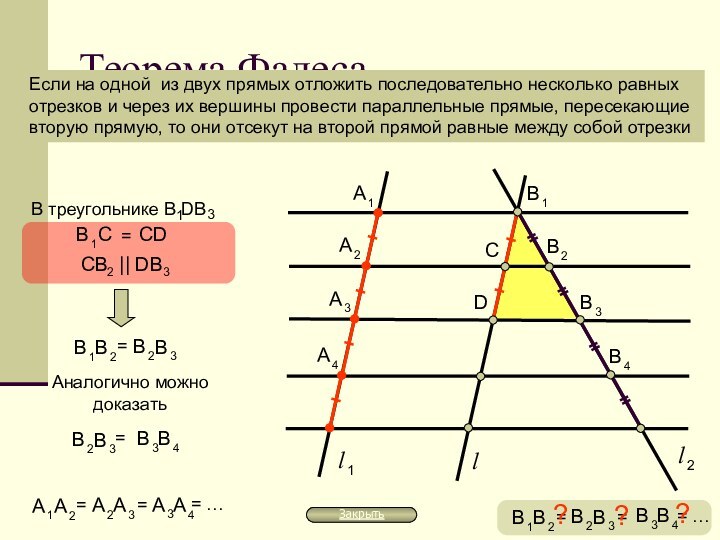
философии и науки, основатель
милетской школы.
Сочинения Фалеса не
сохранились, однако Аристотель называет его первым ионийским философом.
Важнейшей заслугой Фалеса в области математики
считается перенесение им из Египта в Грецию первых
начал теоретической элементарной геометрии:
• Вертикальные углы равны.
• Углы при основании равнобедренного треугольника равны.
• Треугольник определяется стороной и прилежащими к ней двумя углами.
• Диаметр делит круг на две равные части.
Фалесу приписывается решение двух геометрических задач практического
характера: определения расстояния корабля на море от Милетской гавани и
определения высоты пирамиды по длине её тени.