- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему тест Вписанная и описанная окружность
Содержание
- 2. 1. Центр вписанной в треугольник окружности совпадает с точкой пересечения…медианбиссектриссерединный перпендикуляровпроверка
- 3. сторон треугольника2. Центр вписанной в треугольник окружности равноудален от…углов треугольникавершин треугольникапроверка
- 4. 3. Центр вписанной в треугольник окружности является точкой пересечения его медиан. Этот треугольник…равнобедренныйпрямоугольныйравносторонний
- 5. 4. Окружность называется вписанной в многоугольник, если…
- 6. 5. Центр описанной окружности около треугольника – это точка пересечения…высотбиссектриссерединных перпендикуляровпроверка
- 7. 6. Радиус описанной около треугольника окружности равен расстоянию от центра окружности до… углов треугольникавершин треугольникасторон треугольникапроверка
- 8. 7. Центр описанной около равнобедренного треугольника окружности
- 9. 8. Центр описанной около прямоугольного треугольника окружности лежит на…середине гипотенузысередине катетагипотенузепроверка
- 10. 9. Четырехугольник можно вписать в окружность, если…суммы противолежащих углов равны 180°суммы противолежащих сторон равныпротиволежащие стороны равныпроверка
- 11. 10. В четырехугольник можно вписать окружность, если…противолежащие стороны равнысуммы противолежащих сторон равныпротиволежащие углы равныпроверка
- 12. 11. Прямоугольник. Окружность можно… описатьничего нельзя сделатьвписатьпроверка
- 13. 12. Сторона равностороннего треугольника равна 12см. Радиус вписанной окружности равен… свой ответ2√34√3
- 14. В любой треугольник можно вписать окружность и
- 15. В любой треугольник можно вписать окружность и
- 16. Если все стороны многоугольника касаются окружности, то
- 17. Около любого треугольника можно описать окружность и
- 18. Около любого треугольника можно описать окружность и
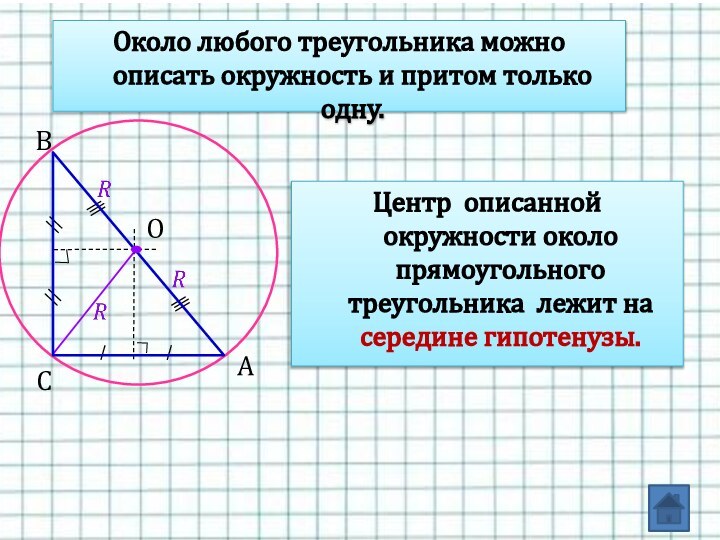
- 19. Около любого треугольника можно описать окружность и
- 20. Дано: окр.(О;R) описанна около четырехугольник ABCDДоказательство:
- 21. В четырехугольник можно вписать окружность тогда и
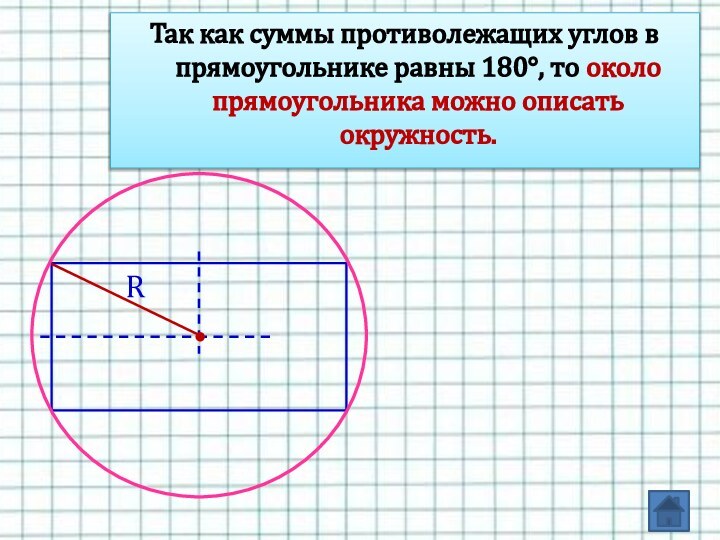
- 22. Так как суммы противолежащих углов в прямоугольнике равны 180°, то около прямоугольника можно описать окружность. R
- 23. Скачать презентацию
- 24. Похожие презентации
1. Центр вписанной в треугольник окружности совпадает с точкой пересечения…медианбиссектриссерединный перпендикуляровпроверка













Слайд 3
сторон треугольника
2. Центр вписанной в треугольник окружности равноудален
от…
углов треугольника
вершин треугольника
проверка
Слайд 4 3. Центр вписанной в треугольник окружности является точкой
пересечения его медиан. Этот треугольник…
равнобедренный
прямоугольный
равносторонний
Слайд 5
4. Окружность называется вписанной в многоугольник, если…
все
его вершины лежат на окружности
все его стороны имеют общие
точки с окружностью
все его стороны касаются
окружности
проверка
Слайд 6 5. Центр описанной окружности около треугольника – это
точка пересечения…
высот
биссектрис
серединных перпендикуляров
проверка
Слайд 7 6. Радиус описанной около треугольника окружности равен расстоянию
от центра окружности до…
углов треугольника
вершин треугольника
сторон треугольника
проверка
Слайд 8 7. Центр описанной около равнобедренного треугольника окружности может
лежать…
на одной из его медиан
на любой из его
биссектрисна любой из его высот
Слайд 9 8. Центр описанной около прямоугольного треугольника окружности лежит
на…
середине гипотенузы
середине катета
гипотенузе
проверка
Слайд 10
9. Четырехугольник можно вписать в окружность, если…
суммы противолежащих
углов равны 180°
суммы противолежащих сторон равны
противолежащие стороны равны
проверка
Слайд 11
10. В четырехугольник можно вписать окружность, если…
противолежащие стороны
равны
суммы противолежащих сторон равны
противолежащие углы равны
проверка
Слайд 13 12. Сторона равностороннего треугольника равна 12см. Радиус вписанной
окружности равен…
свой ответ
2√3
4√3
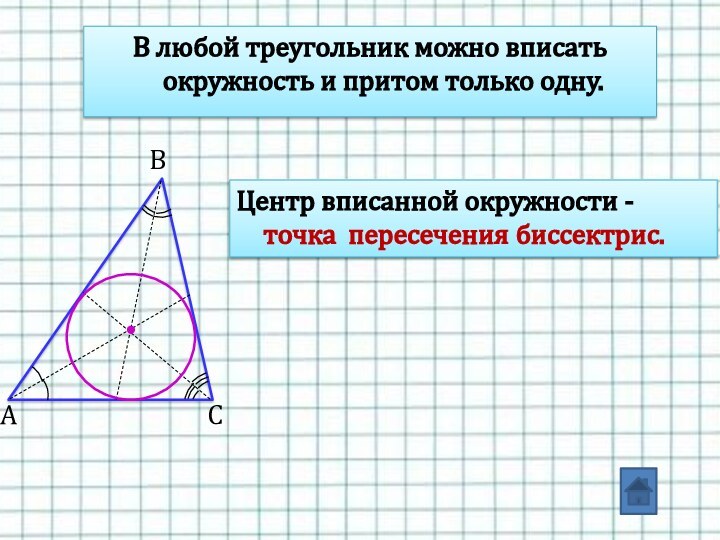
Слайд 14 В любой треугольник можно вписать окружность и притом
только одну.
А
В
С
Центр вписанной окружности - точка пересечения биссектрис.
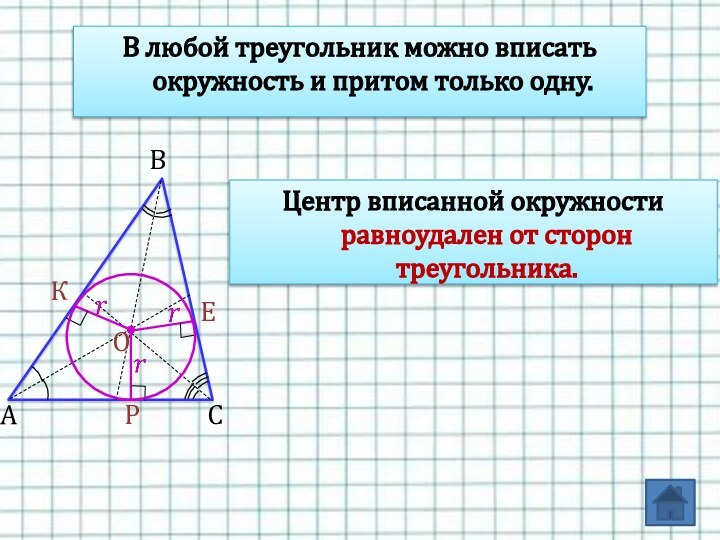
Слайд 15 В любой треугольник можно вписать окружность и притом
только одну.
А
В
С
О
К
Е
Р
Центр вписанной окружности равноудален от сторон треугольника.
Слайд 16
Если все стороны многоугольника касаются
окружности, то окружность
называется
вписанной в многоугольник, а многоугольник –
описанным около
этой окружности.окр.(О;r) вписана в ABCD
А
В
С
D
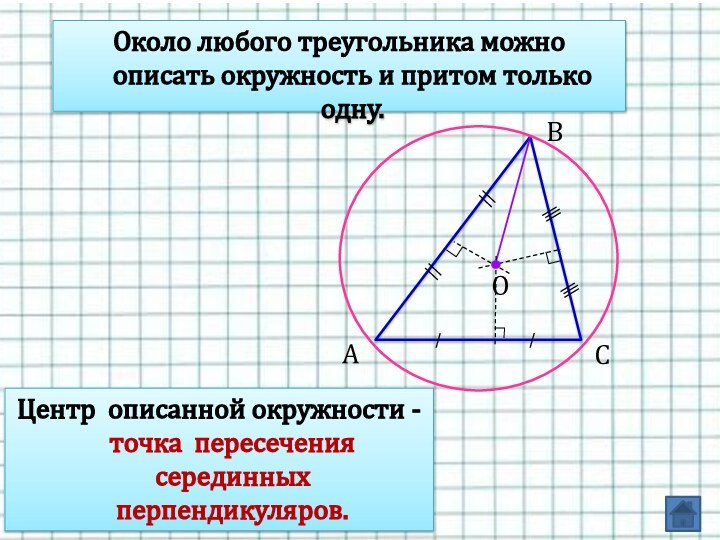
Слайд 17 Около любого треугольника можно описать окружность и притом
только одну.
А
В
С
О
Центр описанной окружности - точка пересечения серединных
перпендикуляров. Слайд 18 Около любого треугольника можно описать окружность и притом
только одну.
А
В
С
О
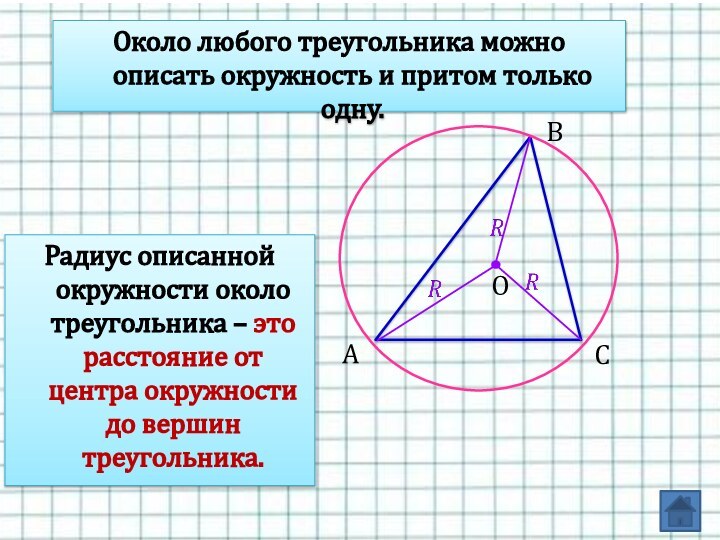
Радиус описанной окружности около треугольника – это
расстояние от центра окружности до вершин треугольника. Слайд 19 Около любого треугольника можно описать окружность и притом
только одну.
А
В
С
О
Центр описанной окружности около прямоугольного треугольника лежит
на середине гипотенузы. Слайд 21 В четырехугольник можно вписать окружность тогда и только
тогда, когда суммы противоположных сторон равны.
А
В
С
D
Дано: окр.(О;r) вписана
в ABCDДоказательство:
Доказать: AB + CD = BC + AD
a
a
b
b
c
c
d
d
AB + CD = a + b + c + d
BC + AD = a + b + c + d
AB + CD = BC + AD
обозначим равные
отрезки касательных буквами:
а, b, c, d





























