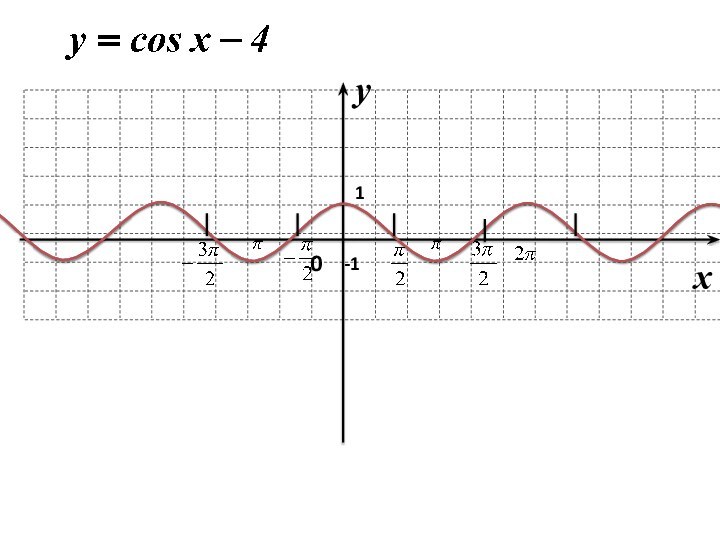
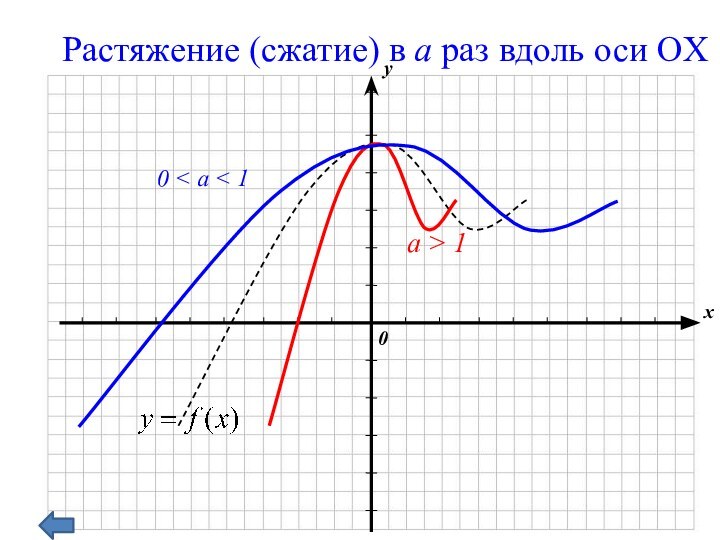
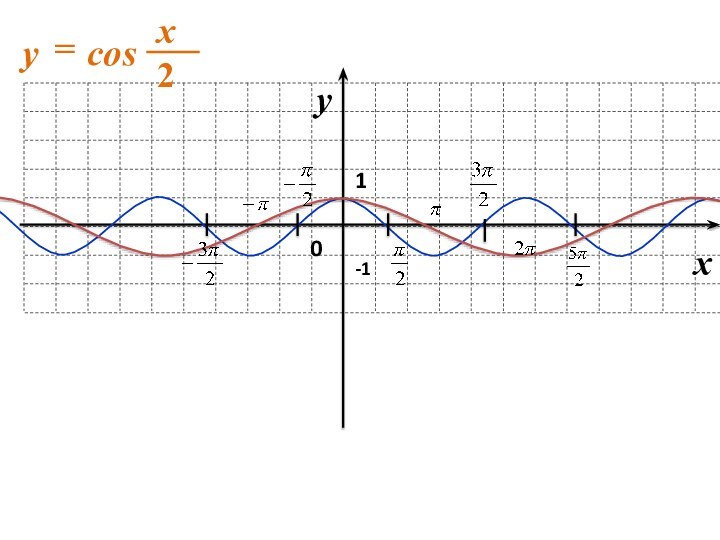
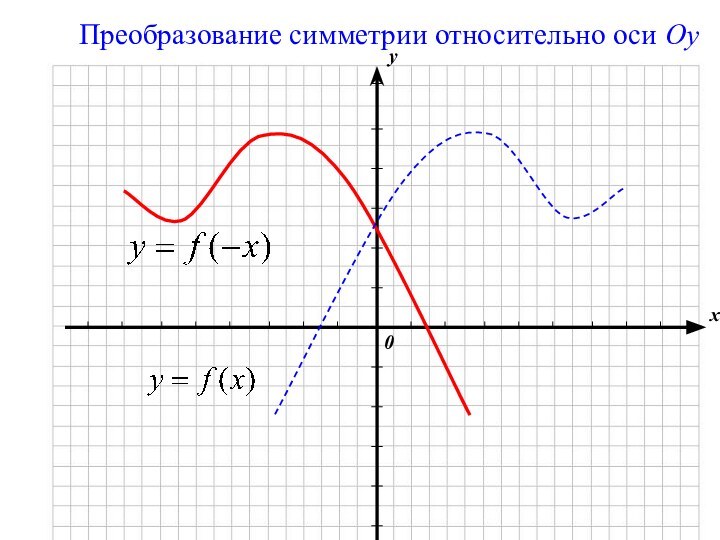
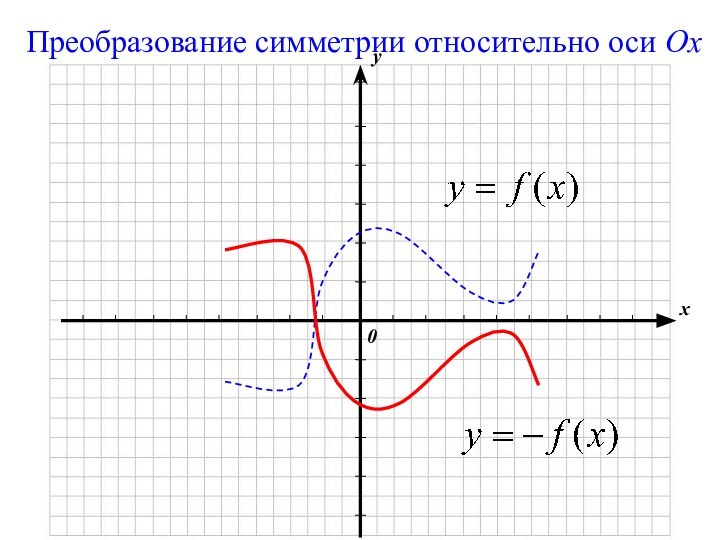
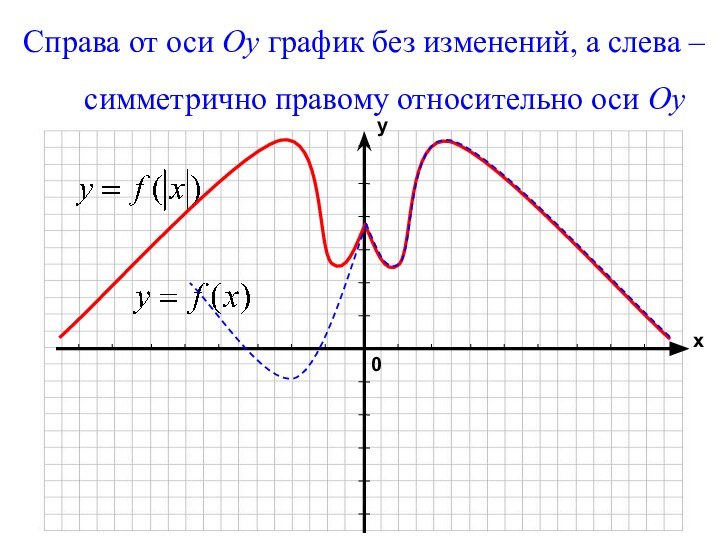
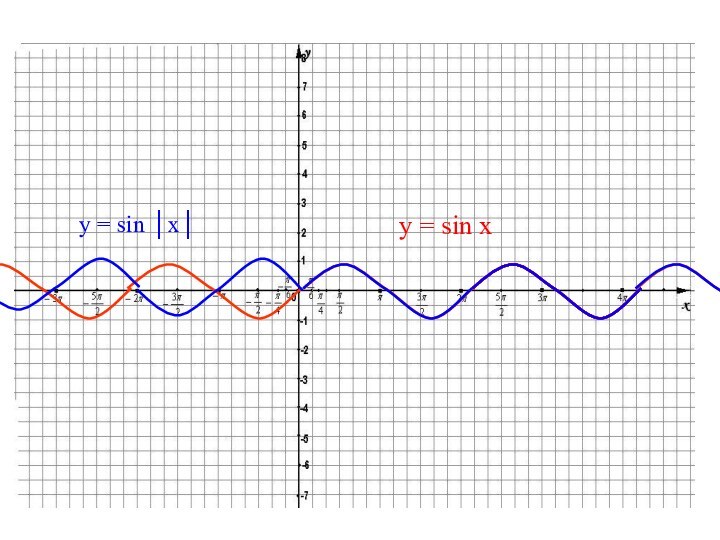
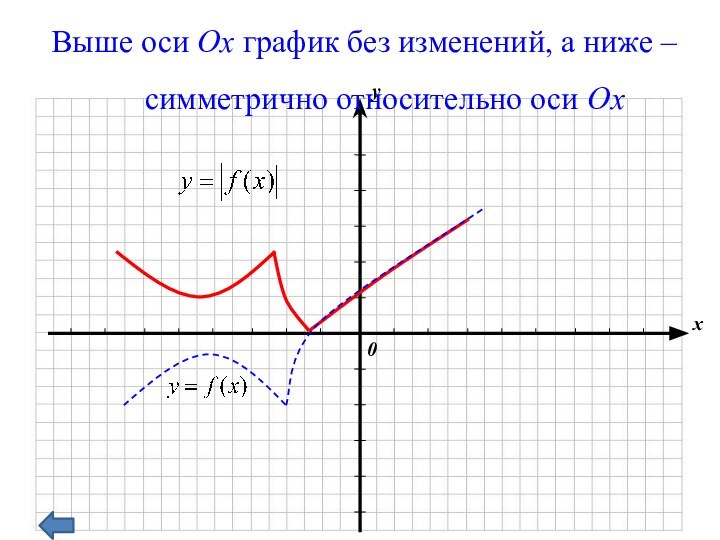
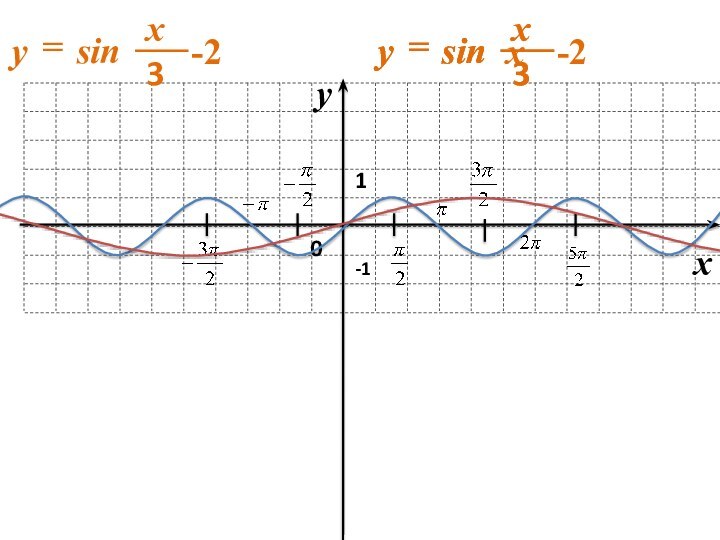
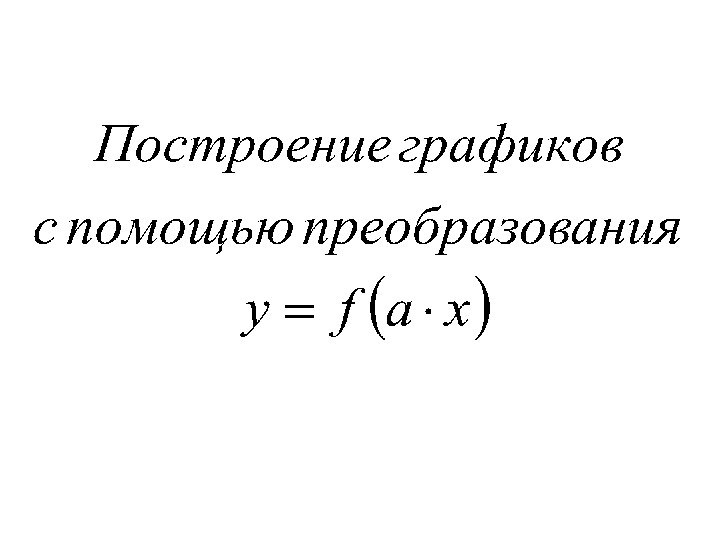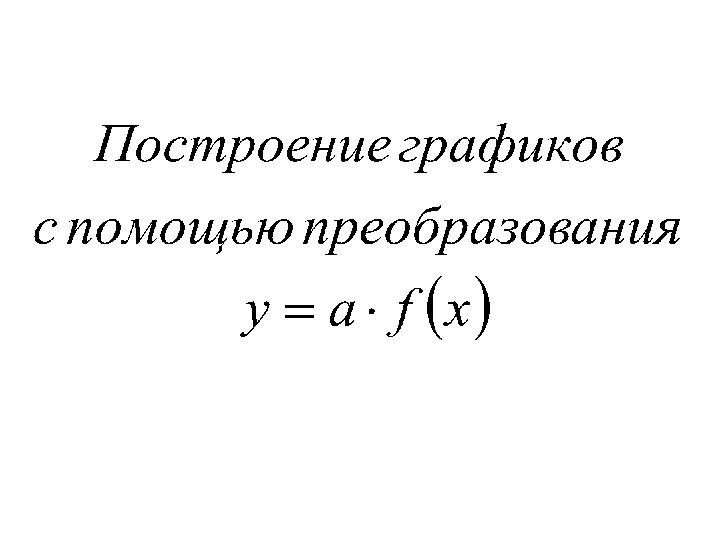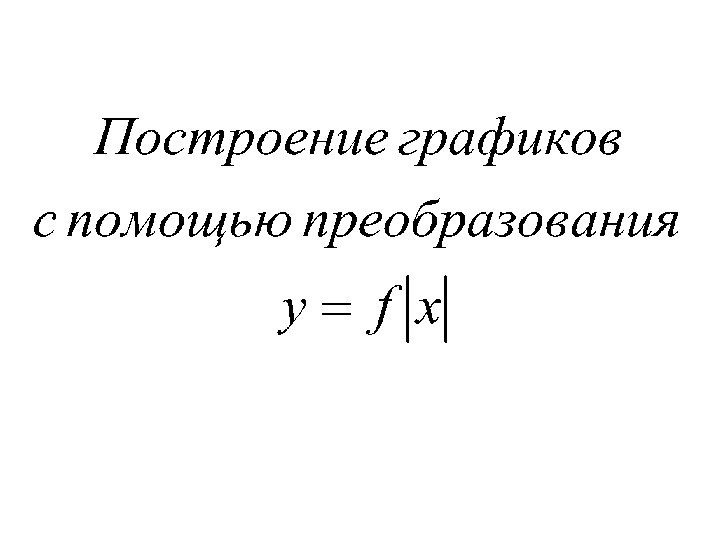геометрические преобразования графиков функций
Научится строить графики сложных функций
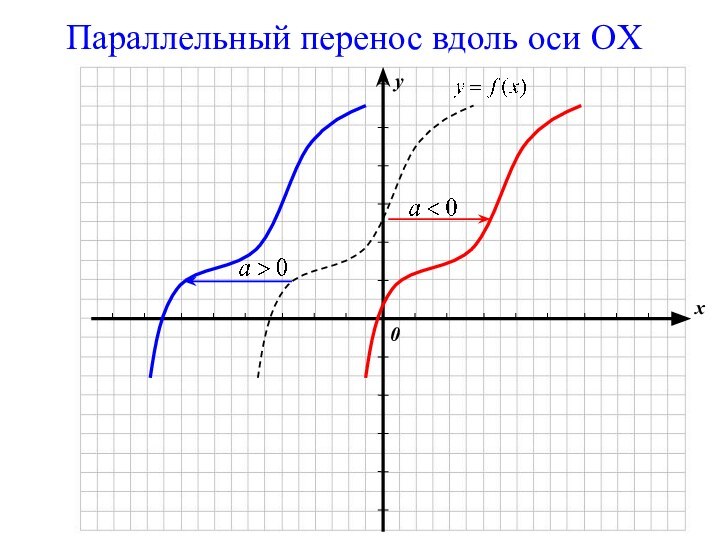
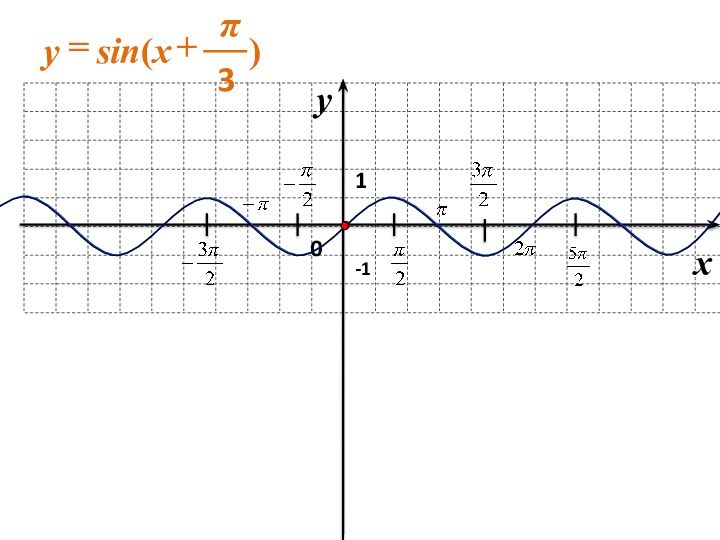
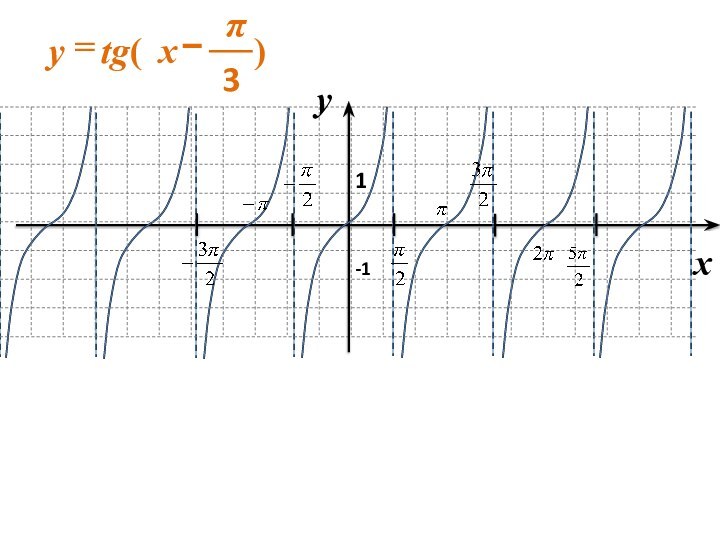
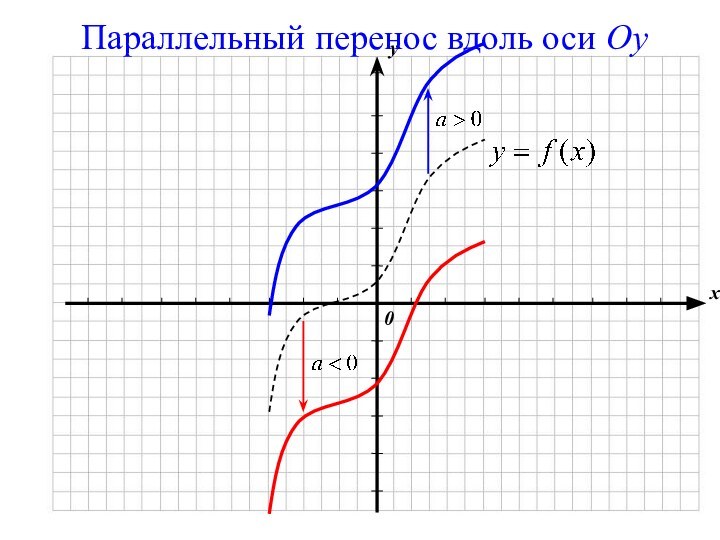
с использованием параллельного переноса, растяжения, сжатия, симметрии относительно осей координат графиков известных функций, показать построение графиков, содержащих модуль, а также с последовательным применением нескольких способов.прививать интерес к математике;
воспитывать графическую культуру, умение видеть красоту математики.