- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок-презентация Уравнение плоскости
Содержание
- 2. Уравнение плоскостиПреподаватель математики Семяшкина Ирина Васильевна ГПОУ «Ижемкий политехнический техникум»
- 3. Цель:познакомить учащихся с понятием уравнения плоскости
- 4. Проверка готовности.Греческий, латинский3 (аксиома А1), (ABC)Параллельно, пересекаться, совпадать
- 5. Общее уравнение плоскостиAx+By+Cz+D=0где А, В, С, D – числовые коэффициенты
- 6. Уравнения координатных плоскостей x = 0,
- 7. Особые случаи уравнения:D = 0 Ax+By+Cz
- 8. Особые случаи уравнения:А = В = 0
- 9. Особые случаи уравнения:A = D = 0
- 10. совпадают, если существует такое число k,
- 11. Алгоритм составления уравнения плоскости, проходящей через
- 12. Если известна какая-нибудь точка плоскости
- 13. Чтобы получить уравнение плоскости, имеющее
- 14. Пример 1. Составить уравнение плоскости, проходящей
- 15. Уравнение плоскости, проходящей через три точки
- 16. Пример 2. Составить уравнение плоскости, проходящей через
- 17. При равенстве нулю свободного коэффициента D уравнения
- 18. Вектор нормали это…Всякий ненулевой векторВсякий перпендикулярный ненулевой векторВсякий перпендикулярный плоскости ненулевой векторВсякий перпендикулярный плоскости вектор
- 19. Общее уравнение плоскости это… Ax+By+Cz=0 Ax+By+Cz=D Ax+By+Cz+D=0 A(x-x0)+B(y-y0)+C(z-z0)=0
- 20. Домашнее задание рассмотреть другие способы нахождения уравнения
- 21. Используемые ресурсы:ПЛОСКОСТИ http://kramshifer.Ub.Ua/ru/board/view/38313/ГЛАДЬ РЕКИ http://www.Raschetrasstoyanie.Com/%D0%A2%D0%BE%D0%BB%D1%81%D1%82%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D0%B9_%D0%9B%D0%B8%D1%81%D0%BA%D0%B8/%D1%84%D0%BE%D1%82%D0%BEПЛОСКИЕ КАМНИ http://aqueouspic.Ru/smotret-komedii-romanticheskie-onlajn.HtmlШАХМАТНАЯ ДОСКА http://www.1chess.Ru/index.Php?Show_aux_page=45СМАЙЛИКИ http://www.baby.ru/blogs/post/314439509-43854232/
- 22. ЕЩЁ ПОДУМАЙте...
- 23. Правильно!!!
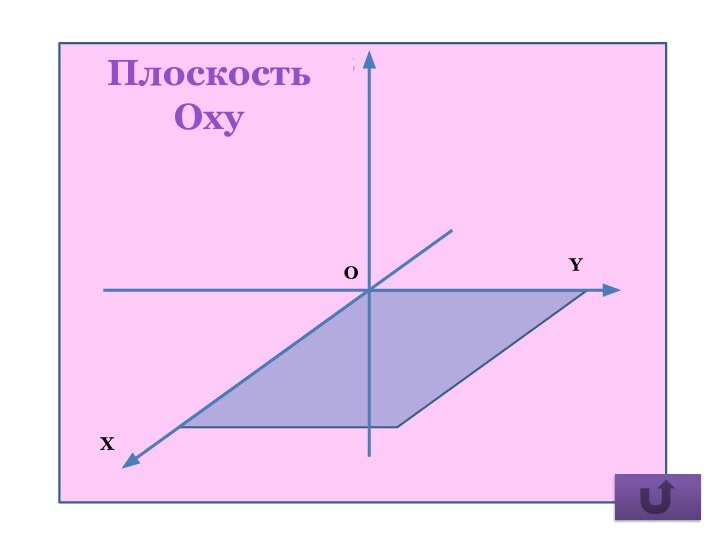
- 24. Плоскость Oхy
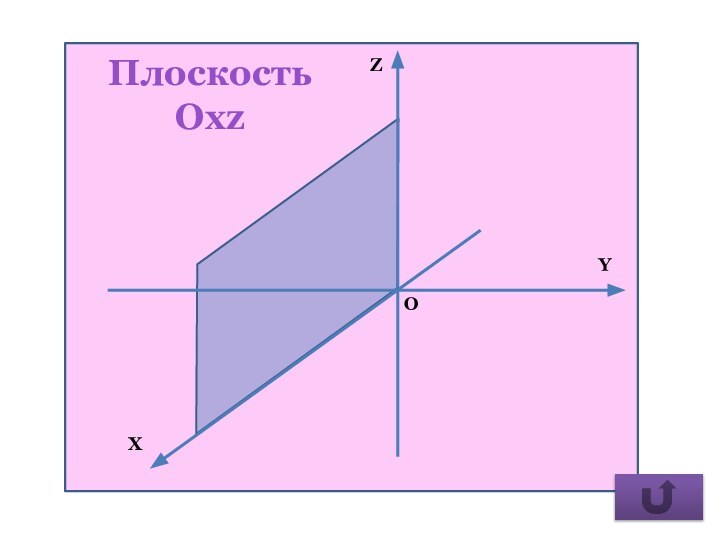
- 25. Плоскость Oхz
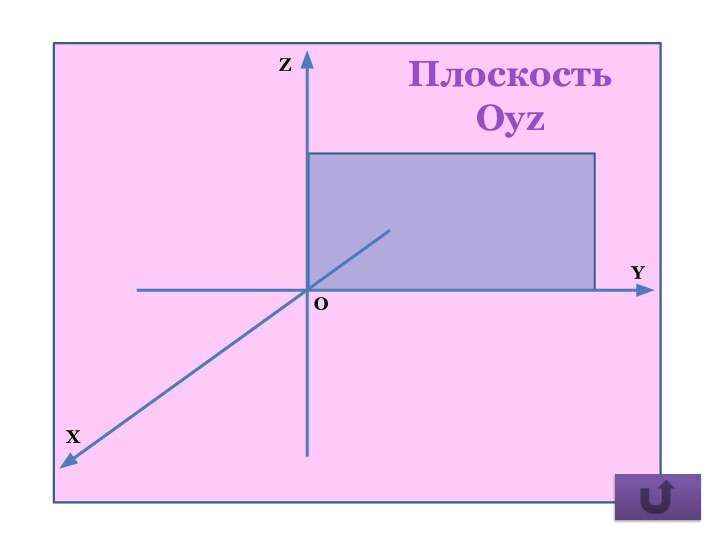
- 26. Плоскость Oyz
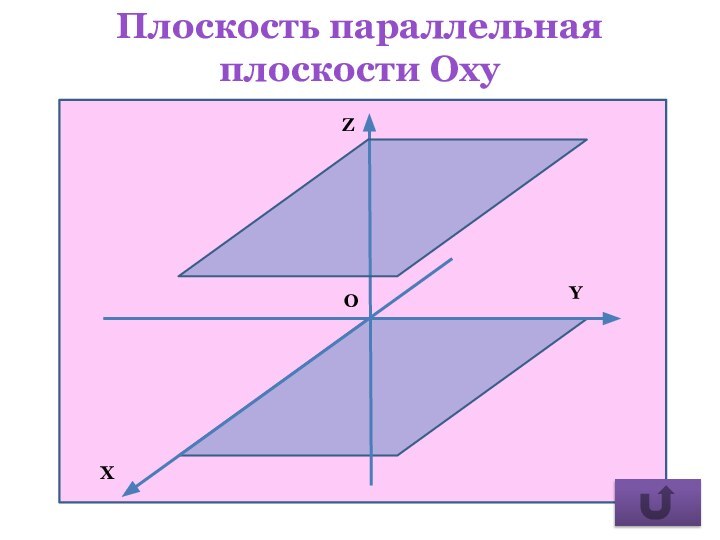
- 27. Плоскость параллельная плоскости Охy
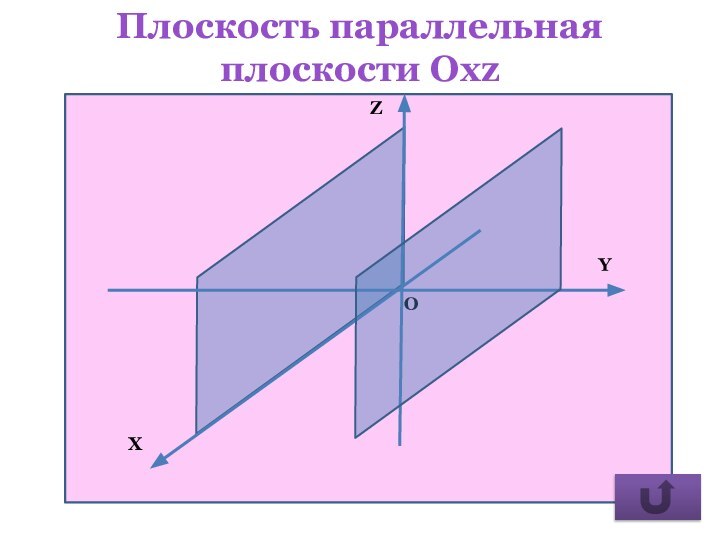
- 28. Плоскость параллельная плоскости Охz
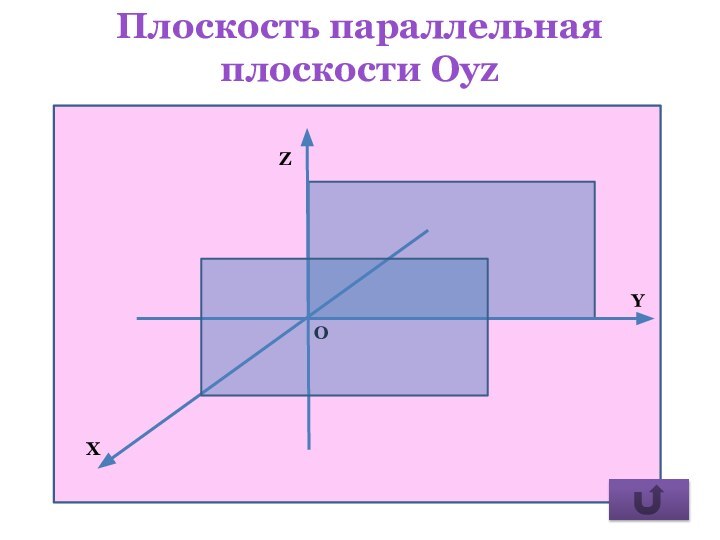
- 29. Плоскость параллельная плоскости Оyz
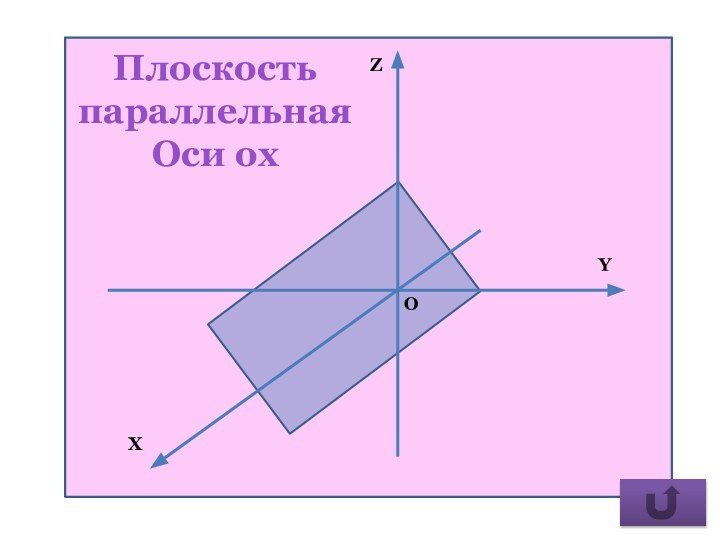
- 30. Плоскость параллельная Оси ох
- 31. Скачать презентацию
- 32. Похожие презентации
Уравнение плоскостиПреподаватель математики Семяшкина Ирина Васильевна ГПОУ «Ижемкий политехнический техникум»
Слайд 2
Уравнение плоскости
Преподаватель математики
Семяшкина Ирина Васильевна
ГПОУ «Ижемкий
политехнический техникум»
Слайд 3
Цель:
познакомить учащихся с понятием уравнения плоскости и
её особыми случаями задания;
Выработать практические навыки по изучаемой теме
при решении задач.
Слайд 4
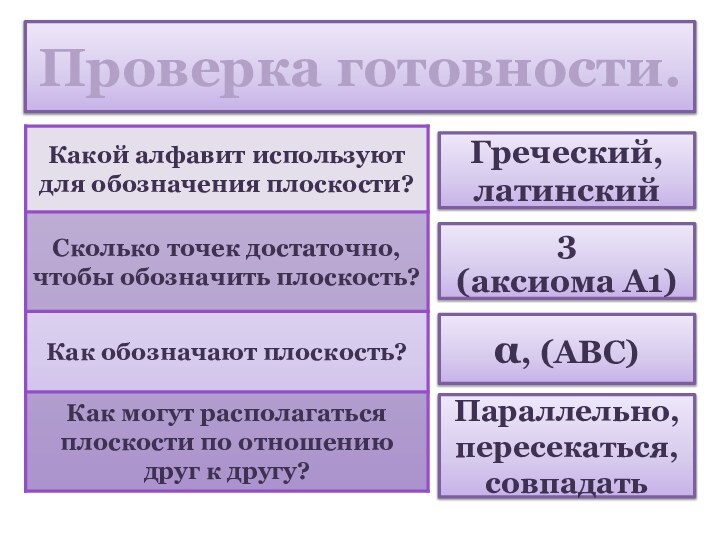
Проверка готовности.
Греческий, латинский
3
(аксиома А1)
, (ABC)
Параллельно, пересекаться, совпадать
Слайд 6
Уравнения координатных плоскостей
x = 0, плоскость
Оyz
y = 0, плоскость Оxz
z = 0, плоскость Оxy
Слайд 7
Особые случаи уравнения:
D = 0 Ax+By+Cz =
0
плоскость проходит через начало координат.
А = 0 Ву + Cz +D = 0
плоскость параллельна оси Ох.
В = 0 Ах + Cz +D = 0
плоскость параллельна оси Оу.
C = 0 Ax+By+D = 0
плоскость параллельна оси Oz.
Слайд 8
Особые случаи уравнения:
А = В = 0
Сz + D = 0
плоскость параллельна плоскости Оху.
А = С = 0 Ву + D = 0
плоскость параллельна плоскости Охz.
В = C= 0 Ах+D = 0
плоскость параллельна плоскости Оуz.
Слайд 9
Особые случаи уравнения:
A = D = 0
By+Cz = 0
плоскость проходит через ось Ox.
B = D = 0 Ax + Cz = 0
плоскость параллельна оси Оy.
C = D = 0 Ах + By = 0
плоскость параллельна оси Оz.
Слайд 10
совпадают, если существует такое число k, что
Две
плоскости в пространстве:
параллельны, если существует такое число k,
что В остальных случаях плоскости пересекаются.
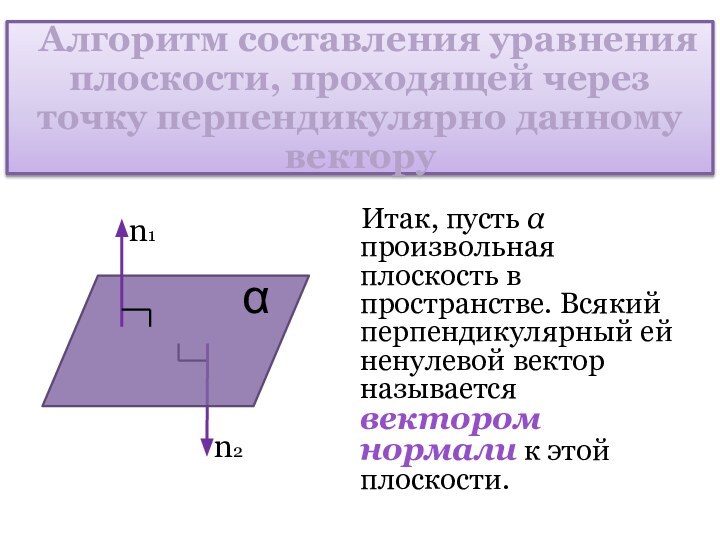
Слайд 11 Алгоритм составления уравнения плоскости, проходящей через точку
перпендикулярно данному вектору
Итак, пусть произвольная плоскость
в пространстве. Всякий перпендикулярный ей ненулевой вектор называется вектором нормали к этой плоскости.
Слайд 12 Если известна какая-нибудь точка плоскости M0
и какой-нибудь вектор нормали к ней, то через заданную
точку можно провести единственную плоскость, перпендикулярную данному вектору. Общее уравнение плоскости будет иметь вид: Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору
M0
A(x-x0)+B(y-y0)+C(z-z0)=0
Слайд 13 Чтобы получить уравнение плоскости, имеющее приведённый
вид, возьмём на плоскости произвольную точку M(x;y;z). Эта точка
принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис), а для этого, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е.Вектор задан по условию. Координаты вектора найдём по формуле :
Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:
A(x-x0)+B(y-y0)+C(z-z0)=0
Слайд 14 Пример 1. Составить уравнение плоскости, проходящей через
точку
и перпендикулярной вектору .Используем формулу
A(x-x0)+B(y-y0)+C(z-z0)=0
Решение:
Ответ: 5x + y - 4z - 3=0
Слайд 15
Уравнение плоскости, проходящей через три точки
После
раскрытия определителя это уравнение становится уравнением общего вида.
Пусть даны
три различные точки, не лежащие на одной прямой. Используя выражение смешанного произведения в координатах, получим уравнение плоскости:
Слайд 16 Пример 2. Составить уравнение плоскости, проходящей через три
данные точки, не лежащие на одной прямой:
; и .Решение:
Ответ: -4y + 2z - 2=0
Слайд 17 При равенстве нулю свободного коэффициента D уравнения общего
уравнения плоскости уравнение определяет
Плоскость, параллельную координатной плоскости Oxy
Плоскость, проходящую
через начало координатПолуплоскость
Линию пересечения плоскостей
ПРОВЕРИМ, ЧТО МЫ ЗАПОМНИЛИ….
Слайд 18
Вектор нормали это…
Всякий ненулевой вектор
Всякий перпендикулярный ненулевой вектор
Всякий
перпендикулярный плоскости ненулевой вектор
Всякий перпендикулярный плоскости вектор
Слайд 19
Общее уравнение плоскости это…
Ax+By+Cz=0
Ax+By+Cz=D
Ax+By+Cz+D=0
A(x-x0)+B(y-y0)+C(z-z0)=0
Слайд 20
Домашнее задание
рассмотреть другие способы нахождения уравнения плоскости;
Решить
задачу: В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания равна
4, и диагональ боковой грани равна 5. Написать уравнение плоскостей А1В1E и плоскости основания призмы.
Слайд 21
Используемые ресурсы:
ПЛОСКОСТИ http://kramshifer.Ub.Ua/ru/board/view/38313/
ГЛАДЬ РЕКИ http://www.Raschetrasstoyanie.Com/%D0%A2%D0%BE%D0%BB%D1%81%D1%82%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D0%B9_%D0%9B%D0%B8%D1%81%D0%BA%D0%B8/%D1%84%D0%BE%D1%82%D0%BE
ПЛОСКИЕ КАМНИ http://aqueouspic.Ru/smotret-komedii-romanticheskie-onlajn.Html
ШАХМАТНАЯ ДОСКА
