Слайд 2
Arduino UNO
Открытая (для всех), простая платформа для
разработки «железяк».
Включает микроконтроллер (ATmega328P http://www.atmel.com/Images/doc8161.pdf)
Стандартный набор аппаратных средств (USB
чип+интерфейс, порты ввода-вывода, кварцевый резонатор, резисторы, конденсаторы и т.д.)
ATmega328P
Микроконтроллер
USB чип
интерфейс
с USB
Порты (пины)
Ввода-вывода
Слайд 3
Arduino UNO
14 дискретных портов ввода/вывода (digital input/output). 0
или 1, т.е. 0 или 5 вольт. Некоторые пины
способны выполнять специфические функции. Например, пины 0 и 1 – последовательный интерфейс; 2 – ШИМ модуляция
6 аналоговых входов
(analog inputs)
МК – мозг системы
Обработка информации
Интерфейс с USB
для взаимодействия с ПК
Дополнительный вход для питания, можно питать от USB
Питание Vdd + GND (земля)
Слайд 4
Двоичная система счисления
Система счисления с основанием 2. Приобрела
большую популярность благодаря развитию вычислительной техники.
В двоичной системе
счисления числа записываются с помощью двух символов (0 и1). Двойка является основанием двоичной системы счисления. Аналогично у десятичной системы основание 10.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
0 = 0*2^0 = 0 – ноль в десятичной системе счисления;
01=0*2^0=1 – единица в десятичной системе счисления;
10=1*2^1+0*2^0=2+0=3 – тройка в десятичной системе счисления;
11=1*2^1+1*2^0=2+1=4 – четверка в десятичной системе счисления;
Слайд 5
Двоичная система счисления
Разложение числа по основанию 10 и
по основанию 2:
1476 = 1 * 103 + 4 *
102 + 7 * 101 + 6 * 100
10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20
Какое максимальное количество значений может принимать двоичное число, содержащее N разрядов?
Максимальное количество значений двоичного числа, содержащего N разрядов, определится как сумма геометрической прогрессии, содержащей N членов, значение первого члена равно 1 (2^0), основание прогрессии равно 2.
Sn=1*(2^N-1)/(2-1)=2^N-1.
8-битное двоичное число может принимать значения в диапазоне от 0 до 255 (2^8-1).
Слайд 6
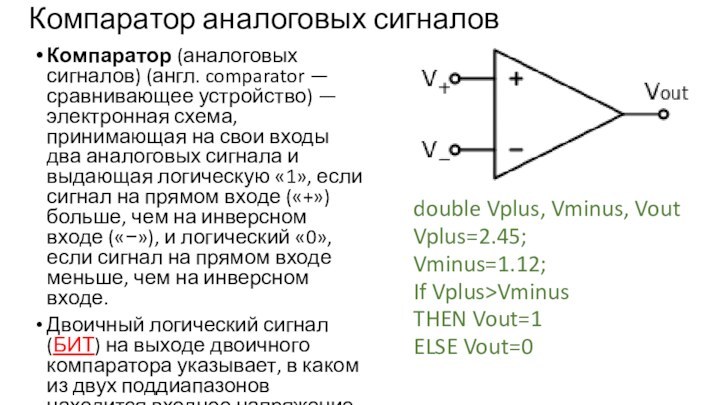
Компаратор аналоговых сигналов
Компаратор (аналоговых сигналов) (англ. comparator — сравнивающее устройство) —
электронная схема, принимающая на свои входы два аналоговых сигнала
и выдающая логическую «1», если сигнал на прямом входе («+») больше, чем на инверсном входе («−»), и логический «0», если сигнал на прямом входе меньше, чем на инверсном входе.
Двоичный логический сигнал (БИТ) на выходе двоичного компаратора указывает, в каком из двух поддиапазонов находится входное напряжение.
double Vplus, Vminus, Vout
Vplus=2.45;
Vminus=1.12;
If Vplus>Vminus
THEN Vout=1
ELSE Vout=0
Слайд 7
АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ (АЦП)
Аналого-цифровой преобразователь (АЦП, Analog-to-digital converter, ADC) — устройство,
преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал).
Обратное преобразование осуществляется при помощи ЦАП ( цифро-аналогового преобразователя, DAC).
Разрешение АЦП — минимальное изменение величины аналогового сигнала, которое может быть преобразовано данным АЦП — связано с его разрядностью.
Разрядность АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе. В двоичных АЦП измеряется в БИТАХ, Например, двоичный 8-разрядный АЦП способен выдать 256 дискретных значений (0…255), поскольку 2^8=256.
Слайд 8
АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ (АЦП)
Разрешение по напряжению равно разности напряжений,
соответствующих максимальному и минимальному выходному коду, делённой на количество
выходных дискретных значений. Всегда должны быть определены максимальное и минимальное (например ноль) значения напряжений, к которым будет «привязываться» АЦП.
Например:
Диапазон входных значений = от 0 до 10 вольт
Разрядность двоичного АЦП 12 бит: 212 = 4096 уровней квантования
Разрешение двоичного АЦП по напряжению: (10-0)/4096 = 0,00244 вольт = 2,44мВ
Рассмотрим (упрощенно) принцип работы трех типов АЦП:
Полностью параллельный АЦП.
Простейший последовательный АЦП.
АЦП последовательного приближения
Слайд 9
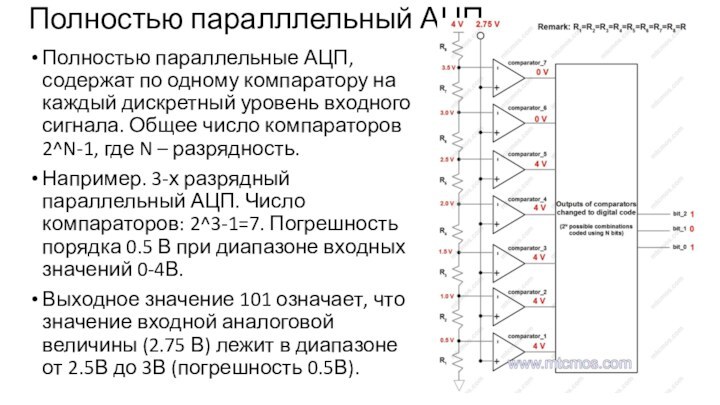
Полностью паралллельный АЦП
Полностью параллельные АЦП, содержат по одному
компаратору на каждый дискретный уровень входного сигнала. Общее число компараторов
2^N-1, где N – разрядность.
Например. 3-х разрядный параллельный АЦП. Число компараторов: 2^3-1=7. Погрешность порядка 0.5 В при диапазоне входных значений 0-4В.
Выходное значение 101 означает, что значение входной аналоговой величины (2.75 В) лежит в диапазоне от 2.5В до 3В (погрешность 0.5В).
Слайд 10
Полностью паралллельный АЦП. Достоинства и недостатки.
Достоинства:
Скорость. Оцифровка выполняется
за один цикл.
Простота. Относительно простые аналоговые элементы (компараторы), простейшая
бинарная логика требуется лишь в конце, чтобы преобразовать последовательность нулей и единиц в выходной бинарный код.
Нет необходимости использовать схему для кратковременного запоминания отсчетов, так как оцифровка выполняется за один цикл. Это очень важно для задач дальнейшей обработки и восстановления сигнала.
Недостатки. По сути, один. Необходимость использования большого количества компараторов в схемах АЦП большой разрядности. Например, если разрядность АЦП N=12, то количество компараторов должно быть равно 2^12-1=4095.
Слайд 11
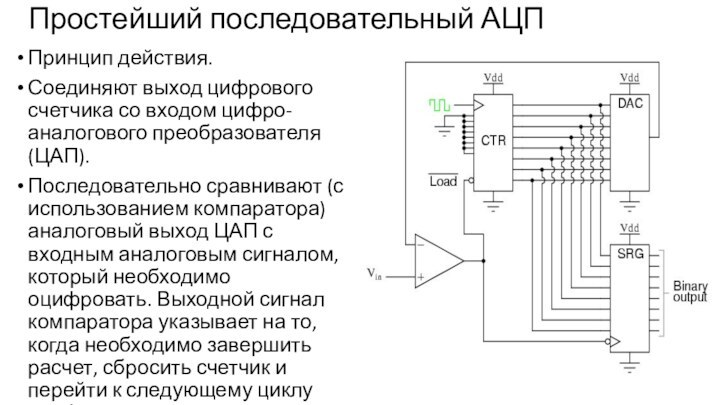
Простейший последовательный АЦП
Принцип действия.
Соединяют выход цифрового счетчика
со входом цифро-аналогового преобразователя (ЦАП).
Последовательно сравнивают (с использованием
компаратора) аналоговый выход ЦАП с входным аналоговым сигналом, который необходимо оцифровать. Выходной сигнал компаратора указывает на то, когда необходимо завершить расчет, сбросить счетчик и перейти к следующему циклу оцифровки.
Слайд 12
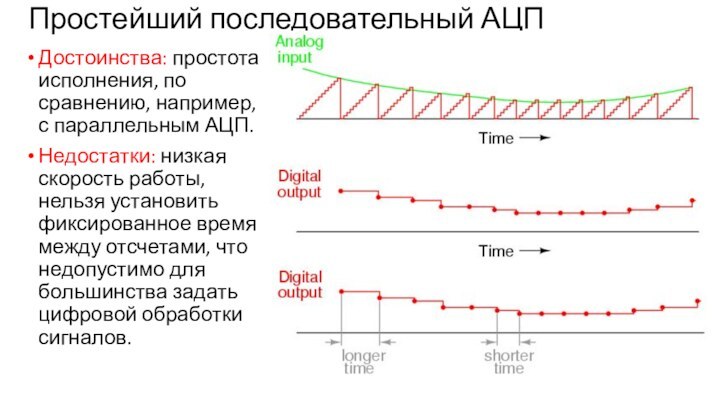
Простейший последовательный АЦП
Достоинства: простота исполнения, по сравнению, например,
с параллельным АЦП.
Недостатки: низкая скорость работы, нельзя установить фиксированное
время между отсчетами, что недопустимо для большинства задать цифровой обработки сигналов.
Слайд 13
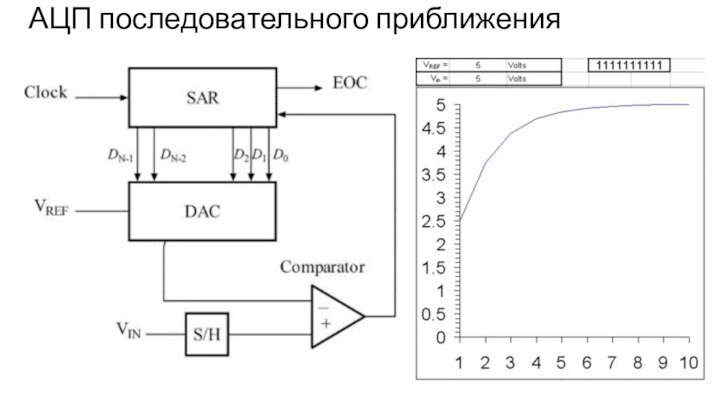
АЦП последовательного приближения
АЦП последовательного приближения обладают относительной простотой,
по сравнению с параллельными АЦП, при этом скорость их
работы выше, по сравнению со скоростью работы последовательных АЦП.
АЦП последовательного приближения использует метод бинарного (двоичного) поиска среди всех доступных ему уровней квантования, повышая тем самым скорость оцифровки входного сигнала.
Бинарный (двоичный) поиск (метод деления пополам) – классический алгоритм поиска элемента в отсортированном массиве (векторе), использующий дробление массива на половины.
Слайд 14
АЦП последовательного приближения
Слайд 15
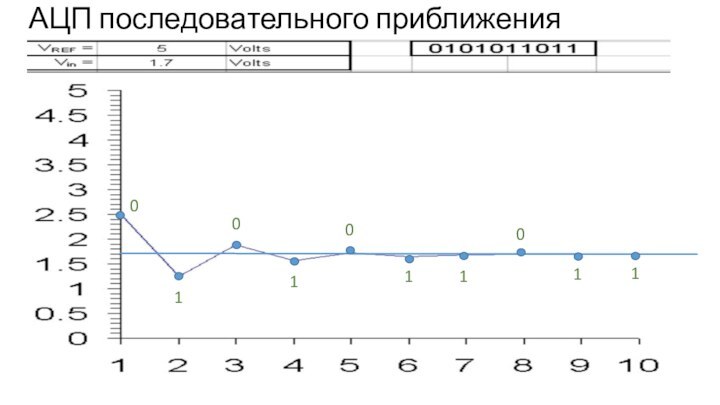
АЦП последовательного приближения
0
1
0
1
0
1
1
0
1
1
Слайд 16
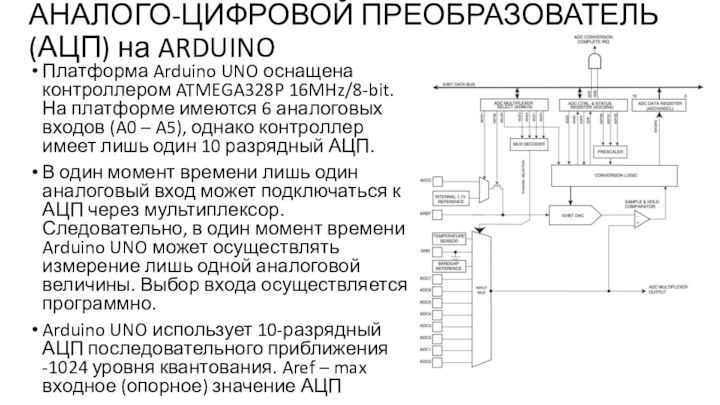
АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ (АЦП) на ARDUINO
Платформа Arduino UNO оснащена
контроллером ATMEGA328P 16MHz/8-bit. На платформе имеются 6 аналоговых входов
(A0 – A5), однако контроллер имеет лишь один 10 разрядный АЦП.
В один момент времени лишь один аналоговый вход может подключаться к АЦП через мультиплексор. Следовательно, в один момент времени Arduino UNO может осуществлять измерение лишь одной аналоговой величины. Выбор входа осуществляется программно.
Arduino UNO использует 10-разрядный АЦП последовательного приближения -1024 уровня квантования. Aref – max входное (опорное) значение АЦП
Слайд 17
Скорость оцифровки сигнала.
ATMEGA328P’s 10-bit ADC необходимо 13 отсчетов
(тактов) для одного аналого-цифрового преобразования.
Однако часы АЦП Arduino UNO
не используют прямые отсчеты времени процессора (16 МГц).
Отсчеты времени АЦП поступают с «делителя», который характеризуется определённым числом. Чаще всего, это число 128 (может быть изменено программно). Таким образом, отсчеты АЦП Arduino UNO выполняются с частотой 16 МГц/128 = 125 кГц или 0.125МГц.
Так как на один цикл АЦП требуется 13 циклов счетчика, следовательно, АЦП будет выполняться с частотой дискретизации 125 кГц/13=9.6 кГц.
Для большинства промышленных АЦП разрядность составляет от 6 до 24 бит, частота дискретизации до 1 МГц.
Слайд 18
Зачем все это нужно???
Возникает большое количество вопросов, связанных
с переходом аналог – цифра – аналог.
Аналоговый сигнал
непрерывен, цифровой - дискретен. Можно ли восстановить исходный аналоговый сигнал из цифровой последовательности единиц и нулей?
Интуитивно понятно, что, по всей видимости, точность восстановления сигнала каким-то образом связана с частотой его оцифровки. Но какова эта связь?
Что вообще подразумевается под восстановлением аналогового сигнала? Какую часть исходной информации мы при этом потеряем?
Что за математика лежит в основе цифро-дискретных преобразований?
и т.д. и т.п…
Слайд 19
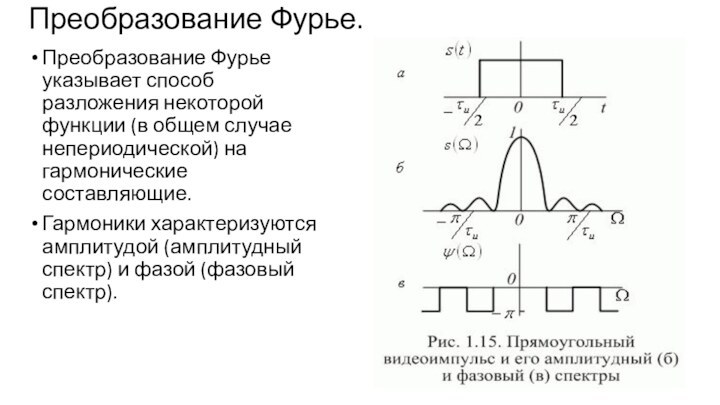
Преобразование Фурье.
Преобразование Фурье указывает способ разложения некоторой функции
(в общем случае непериодической) на гармонические составляющие.
Гармоники характеризуются амплитудой
(амплитудный спектр) и фазой (фазовый спектр).
Слайд 20
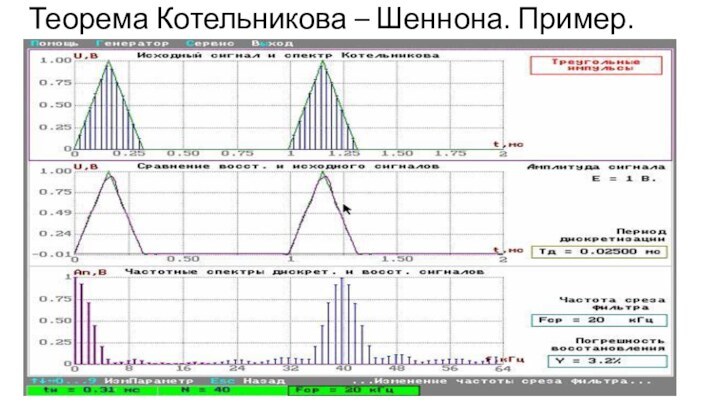
Теорема Котельникова-Шеннона
Теорема связывает непрерывные и дискретные сигналы и
гласит, что любую функцию F(t), состоящую из частот от
0 до f1, можно непрерывно передавать с любой точностью при помощи чисел, следующих друг за другом через 1/(2f1) секунд.
Следствия:
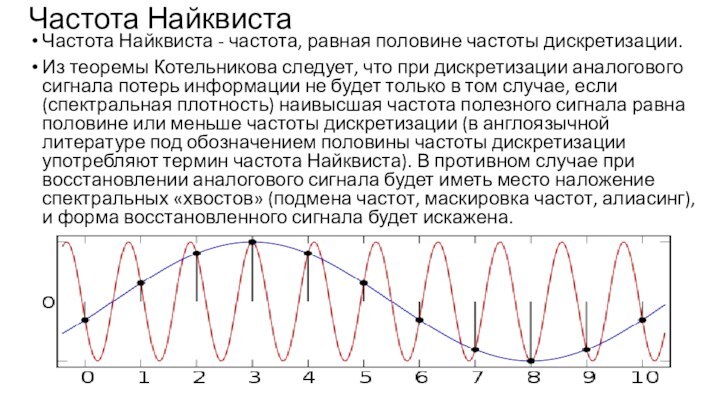
Любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчетам, взятым с частотой f>2fc, где fc – максимальная частота, которой ограничен спектр реального сигнала.
Если максимальная частота в сигнале равна или превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый без искажения не существует.
Слайд 21
Теорема Котельникова – Шеннона. Пример.