Слайд 2
Idea algorytmów ewolucyjnych
Przyjmujemy początkową populację osobników żyjących w
danym środowisku
Za pomocą odpowiednio zdefiniowanej funkcji przystosowania sprawdzamy ich
stopień przystosowania
Osobniki wymieniają miedzy sobą materiał genetyczny i powstają nowe osobniki
Przeżywają osobniki najlepiej przystosowane
Слайд 3
Problemy optymalizacji a algorytmy ewolucyjne
Metody poszukiwania optymalnych rozwiązań:
Analityczne
– rozwiązanie układu równań
Przeglądowe – sprawdzenie całej przestrzeni poszukiwań
Losowe
– losowe sprawdzenie przestrzeni poszukiwań
Слайд 4
Problemy optymalizacji a algorytmy ewolucyjne
Metody ewolucyjne różnią się
od klasycznych następującymi cechami:
Nie przetwarzają bezpośrednio parametrów zadania lecz
ich zakodowaną postać
Korzystają tylko z funkcji celu a nie z jej pochodnych lub innych pomocniczych informacji
Prowadzą przeszukiwanie wychodząc nie z pojedynczego punktu, lecz z pewnej ich populacji
Stosują probabilistyczne a nie deterministyczne reguły wyboru
Слайд 5
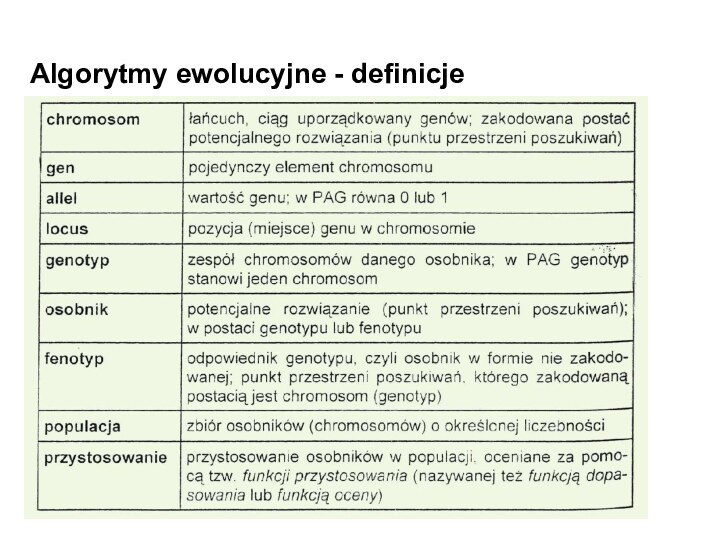
Algorytmy ewolucyjne - definicje
Слайд 6
Operatory genetyczne
Krzyżowanie
Wybieramy pulę rodzicielską i kojarzymy chromosomy w
pary
Losujemy pozycję genu (locus) w chromosomie określającą punkt krzyżowania.
Jeśli każdy z rodziców składa się z L genów to punkt krzyżowania jest liczbą l z zakresu [1,L-1].
W wyniku krzyżowania otrzymuje się parę potomków:
Potomek, którego chromosom składa się z genów na pozycjach od 1 do l pochodzących od pierwszego rodzica i pozostałych genów pochodzących od drugiego rodzica
Potomek, którego chromosom składa się z genów na pozycjach od 1 do l pochodzących od drugiego rodzica i pozostałych genów pochodzących od pierwszego rodzica
Слайд 7
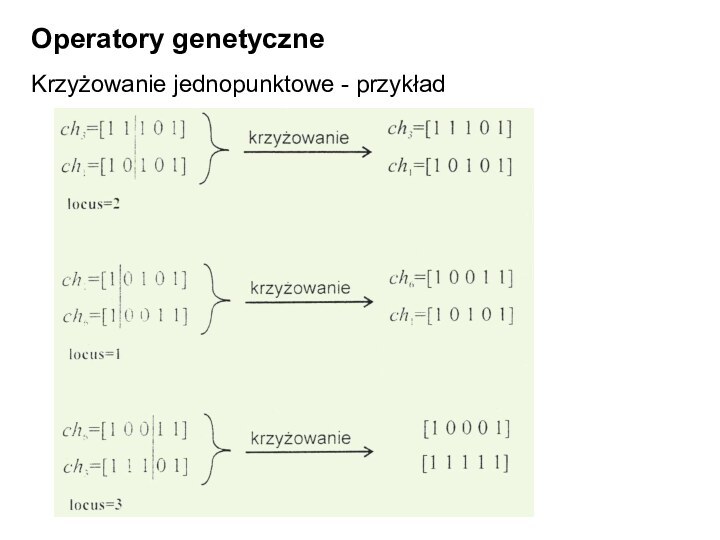
Operatory genetyczne
Krzyżowanie jednopunktowe - przykład
Слайд 8
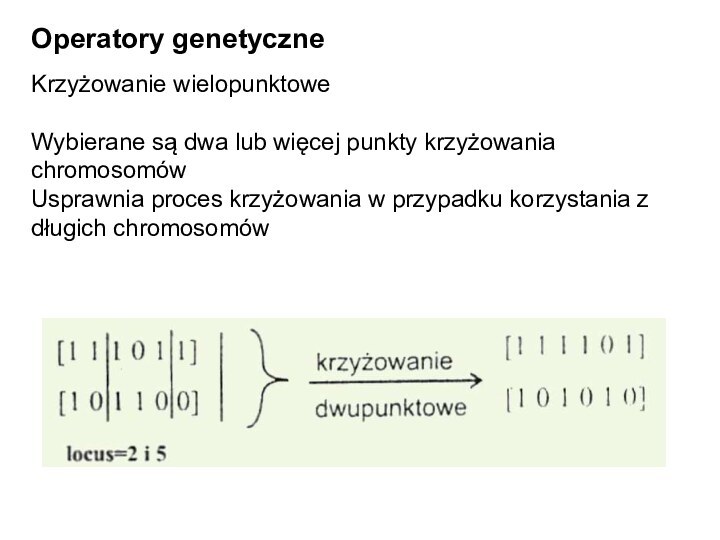
Operatory genetyczne
Krzyżowanie wielopunktowe
Wybierane są dwa lub więcej punkty
krzyżowania
chromosomów
Usprawnia proces krzyżowania w przypadku korzystania z
długich chromosomów
Слайд 9
Operatory genetyczne
Krzyżowanie wielopunktowe dla czterech punktów krzyżowania
Wylosowano następujące
miejsca krzyżowania: 1, 4, 6 i 9.
Слайд 10
Operatory genetyczne
Mutacja
Zmienia wartość wybranego losowo genu w chromosomie
na przeciwny (1 na 0, 0 na 1)
Mutacja zachodzi
bardzo rzadko – prawdopodobieństwo mutacji jest zwykle dużo mniejsze niż krzyżowania
Celem mutacji jest wprowadzenie różnorodności populacji
Слайд 11
Operatory genetyczne
Inwersja
Działa na pojedynczym chromosomie, zmieniając kolejność alleli
między dwoma losowo wybranymi pozycjami chromosomu.
Nie jest to operator
często stosowany w algorytmach genetycznych.
Przykład:
Wylosowano pozycje 4 i 10.
Слайд 13
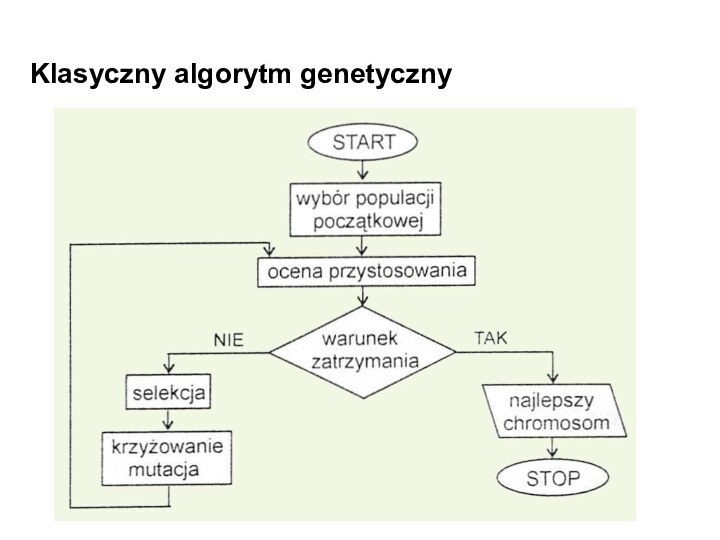
Klasyczny algorytm genetyczny
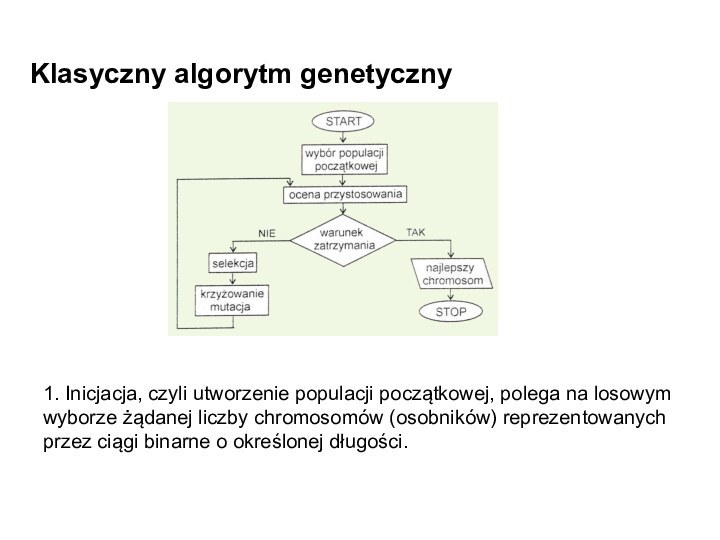
1. Inicjacja, czyli utworzenie populacji początkowej,
polega na losowym wyborze żądanej liczby chromosomów (osobników) reprezentowanych
przez ciągi binarne o określonej długości.
Слайд 14
Klasyczny algorytm genetyczny
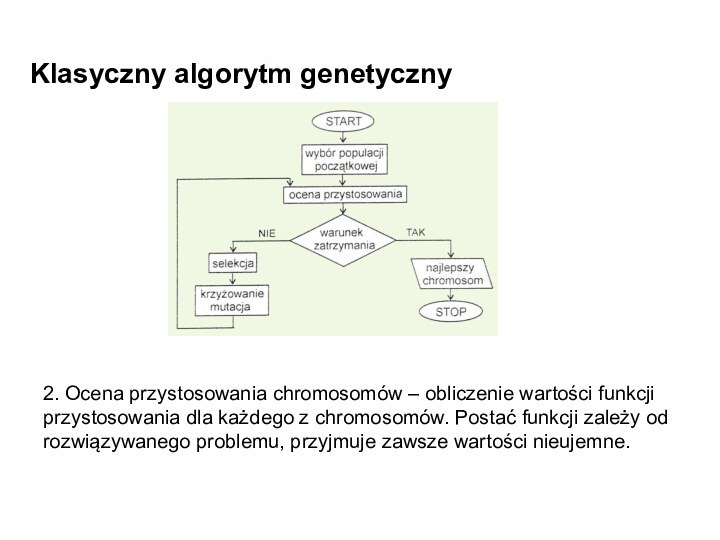
2. Ocena przystosowania chromosomów – obliczenie
wartości funkcji przystosowania dla każdego z chromosomów. Postać funkcji
zależy od rozwiązywanego problemu, przyjmuje zawsze wartości nieujemne.
Слайд 15
Klasyczny algorytm genetyczny
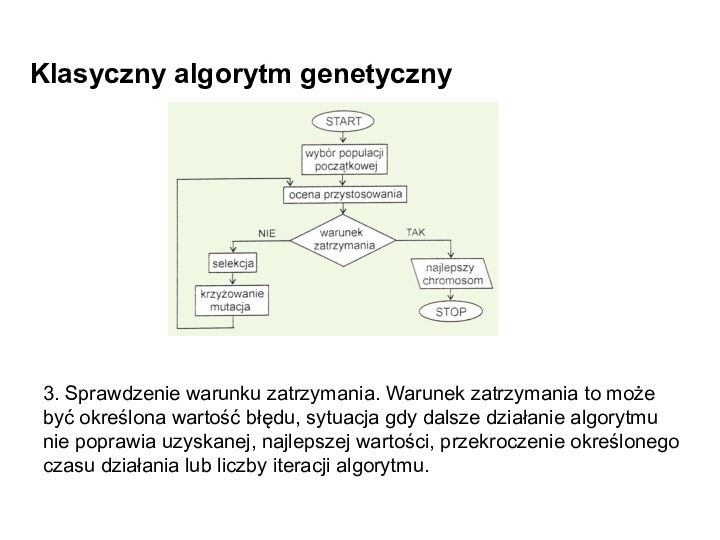
3. Sprawdzenie warunku zatrzymania. Warunek zatrzymania
to może być określona wartość błędu, sytuacja gdy dalsze
działanie algorytmu nie poprawia uzyskanej, najlepszej wartości, przekroczenie określonego czasu działania lub liczby iteracji algorytmu.
Слайд 16
Klasyczny algorytm genetyczny
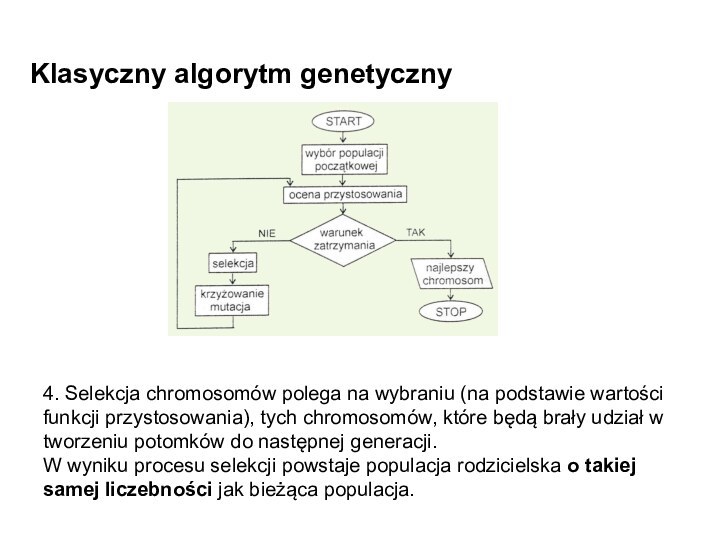
4. Selekcja chromosomów polega na wybraniu
(na podstawie wartości funkcji przystosowania), tych chromosomów, które będą
brały udział w tworzeniu potomków do następnej generacji.
W wyniku procesu selekcji powstaje populacja rodzicielska o takiej samej liczebności jak bieżąca populacja.
Слайд 17
Klasyczny algorytm genetyczny
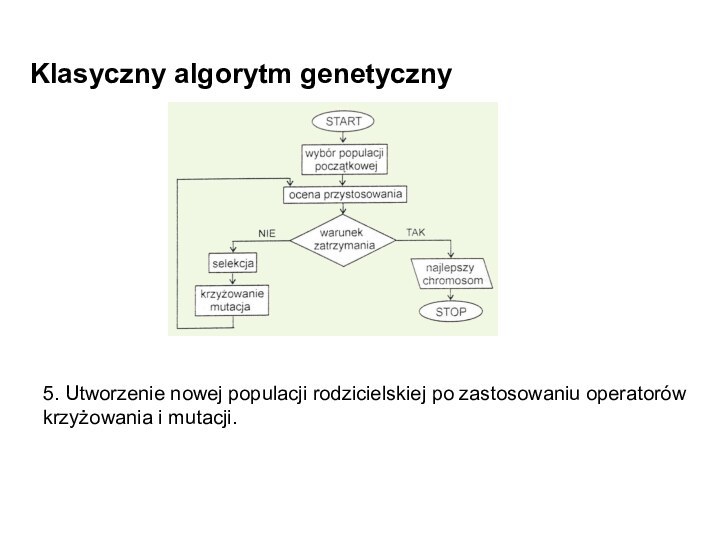
5. Utworzenie nowej populacji rodzicielskiej po
zastosowaniu operatorów krzyżowania i mutacji.
Слайд 18
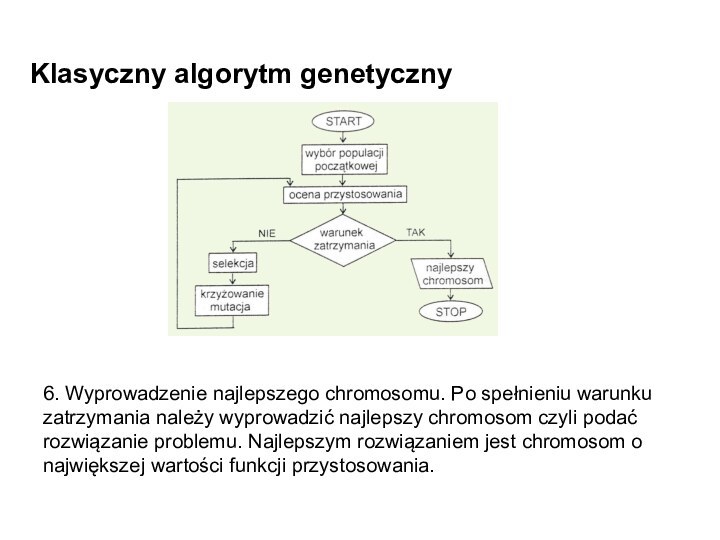
Klasyczny algorytm genetyczny
6. Wyprowadzenie najlepszego chromosomu. Po spełnieniu
warunku zatrzymania należy wyprowadzić najlepszy chromosom czyli podać rozwiązanie
problemu. Najlepszym rozwiązaniem jest chromosom o największej wartości funkcji przystosowania.
Слайд 19
Metody selekcji
Metoda koła ruletki
Selekcja dokonuje się, poprzez wybór
chromosomów, którym na kole (koło ruletki) przydzielono sektory proporcjonalne
do wartości przystosowania
Większa wartość przystosowania = częstszy wybór do populacji rodzicielskiej
Lepiej przystosowane chromosomy mogą być wybierane wielokrotnie
Skutek: miejsce „słabszych” zajmują „mocniejsi”
Слайд 20
Metody selekcji
Metoda koła ruletki
Wielkość sektorów na kole ruletki
przydzielane są według następujących wzorów:
Слайд 21
Metody selekcji
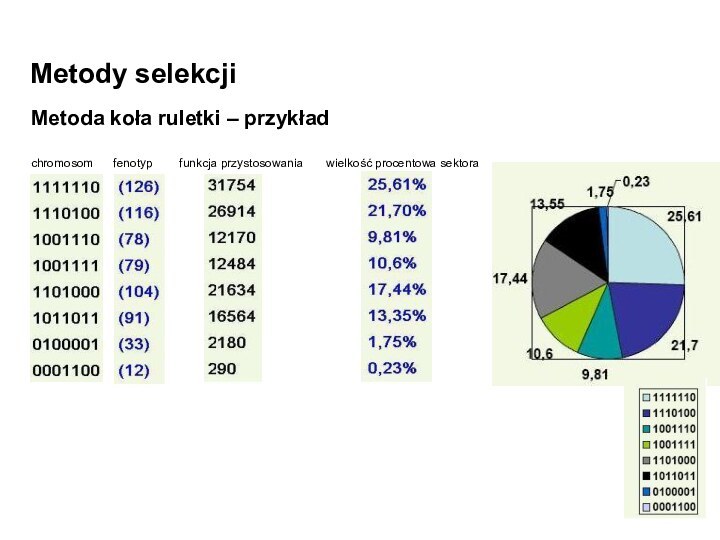
Metoda koła ruletki – przykład
chromosom
fenotyp funkcja przystosowania
wielkość procentowa sektora
Слайд 22
Metody selekcji
Selekcja rankingowa
Osobniki populacji są ustawiane kolejno w
zależności od wartości ich funkcji przystosowania.
Powstaje „lista rankingowa” od
najlepiej do najgorzej przystosowanych osobników (lub odwrotnie).
Każdemu osobnikowi jest przypisana liczba określająca jego pozycję
na liście (ranga).
Liczba kopii każdego osobnika wprowadzana do populacji rodzicielskiej jest ustalana zgodnie z wcześniej zdefiniowaną funkcją i zależy od rangi.
Przykład funkcji:
Слайд 23
Metody selekcji
Selekcja turniejowa
Dzieli się osobniki na grupy a
następnie z każdej grupy wybiera się osobnika o najlepszym
przystosowaniu. Podgrupy mogą być dowolnego rozmiaru (najczęściej 2 lub 3 osobniki).
Selekcja progowa
Modyfikacja selekcji rankingowej, w której funkcja określająca prawdopodobieństwo przejścia osobnika do puli rodzicielskiej ma postać progu. Przykładowa funkcja:
Слайд 24
Algorytm genetyczny – przykład 1
Szukanie maksimum funkcji y=2x+1
dla x∈[0,31]
x – parametr zadania.
Zbiór {0,1,2,...,31} – przestrzeń poszukiwań
a jednocześnie zbiór potencjalnych rozwiązań zadania
Rozwiązania kodujemy binarnie za pomocą 5 bitów.
Ciągi kodowe to chromosomy a w tym przypadku także genotypy.
Jako funkcję przystosowania przyjmiemy y=2x+1
Слайд 25
Algorytm genetyczny – przykład 1
Losujemy populację początkową
W wyniku
losowania otrzymujemy:
co odpowiada fenotypom:
ch1=[00110] ch1*=6
ch2=[00101] ch2*=5
ch3=[01101] ch3*=13
ch4=[10101] ch4*=21
ch5=[11010] ch5*=26
ch6=[10010] ch6*=18
ch7=[01000] ch7*=8
ch8=[00101] ch8*=5
Слайд 26
Algorytm genetyczny – przykład 1
2. Obliczamy funkcję przystosowania
F(ch1)=2•ch1*+1=13
F(ch2)=11
F(ch3)=27
F(ch4)=43
F(ch5)=53
F(ch6)=37
F(ch7)=17
F(ch8)=11
Suma=212
Слайд 27
Algorytm genetyczny – przykład 1
3. Selekcja chromosomów –
koło ruletki
Na podstawie wzorów:
obliczamy wycinki koła ruletki wyrażone w
procentach:
v(ch1)=(13/212)•100%=6,13%
v(ch2)=5,19%
v(ch3)=12,74%
v(ch4)=20,28%
v(ch5)=25%
v(ch6)=17,45%
v(ch7)=8,02%
v(ch8)=5,19%
Слайд 28
Algorytm genetyczny – przykład 1
3. Selekcja chromosomów –
koło ruletki
Za pomocą koła ruletki losujemy 8 nowych chromosomów.
Załóżmy,
że wylosowano następujące liczby:
44 9 74 45 86 48 23
Oznacza to wybór następujących chromosomów:
ch6 ch4 ch2 ch6 ch5 ch6 ch5 ch3
Te chromosomy tworzą pulę rodzicielską.
Слайд 29
Algorytm genetyczny – przykład 1
4. Operacje genetyczne
Załóżmy, że
wylosowano prawdopodobieństwo mutacji pm=0,2 i prawdopodobieństwo krzyżowania pk=0,75
Krzyżowanie:
Kojarzymy osobniki
w pary tak jak są ułożone w puli rodzicielskiej. Dla każdej pary losujemy liczbę z przedziału [0,1]. Jeśli dana liczba będzie mniejsza od pk=0,75 to nastąpi krzyżowanie. Załóżmy, że wylosowano: 0,12 0,73 0,65 0,95.
Oznacza to, że trzy pierwsze pary zostaną poddana krzyżowaniu a czwarta para nie.
Dodatkowo dla każdej pary podlegającej krzyżowaniu losujemy punkt krzyżowania (liczba całkowita z przedziału [1,4]).
Слайд 30
Algorytm genetyczny – przykład 1
4. Operacje genetyczne -
krzyżowanie
Uzyskane wyniki:
Pierwsza para rodziców (lk=3) Pierwsza
para potomków
ch6=[10010] [10001]
ch4=[10101] [10110]
Druga para rodziców (lk=4) Druga para potomków
ch2=[00101] [00100]
ch6=[10010] [10011]
Trzecia para rodziców (lk=3) Trzecia para potomków
ch5=[11010] [11010]
ch6=[10010] [10010]
Czwarta para rodziców Czwarta para potomków
ch5=[11010] [11010]
ch3=[01101] [01101]
Слайд 31
Algorytm genetyczny – przykład 1
4. Operacje genetyczne -
krzyżowanie
Po operacji krzyżowania otrzymujemy następującą populację potomków
o fenotypach
ch1=[10001] ch1*=17
ch2=[10110] ch2*=22
ch3=[00100] ch3*=4
ch4=[10011] ch4*=19
ch5=[11010] ch5*=26
ch6=[10010] ch6*=18
ch7=[11010] ch7*=26
ch8=[01101] ch8*=13
Слайд 32
Algorytm genetyczny – przykład 1
4. Operacje genetyczne -
mutacja
Dla każdego osobnika po krzyżowaniu losujemy liczbę z zakresu
od 0 do 1. Załóżmy, że wylosowano
ch1=[10001] 0,56
ch2=[10110] 0,15
ch3=[00100] 0,48
ch4=[10011] 0,59
ch5=[11010] 0,06
ch6=[10010] 0,89
ch7=[11101] 0,39
ch8=[01010] 0,76
Слайд 33
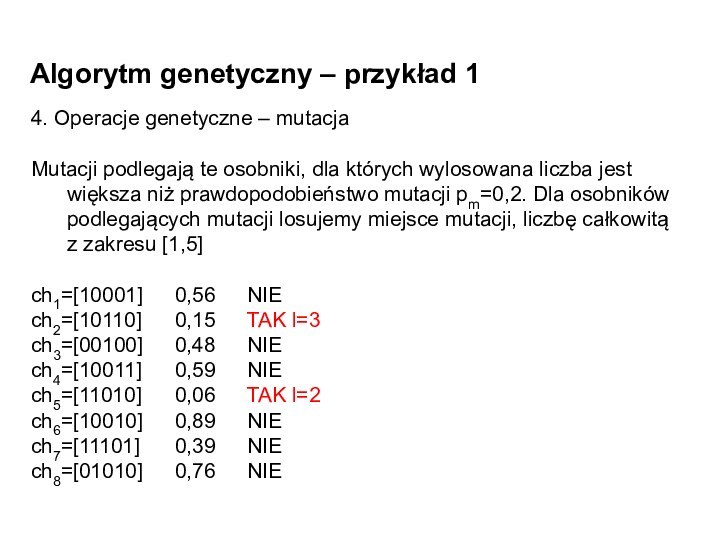
Algorytm genetyczny – przykład 1
4. Operacje genetyczne –
mutacja
Mutacji podlegają te osobniki, dla których wylosowana liczba jest
większa niż prawdopodobieństwo mutacji pm=0,2. Dla osobników podlegających mutacji losujemy miejsce mutacji, liczbę całkowitą z zakresu [1,5]
ch1=[10001] 0,56 NIE
ch2=[10110] 0,15 TAK l=3
ch3=[00100] 0,48 NIE
ch4=[10011] 0,59 NIE
ch5=[11010] 0,06 TAK l=2
ch6=[10010] 0,89 NIE
ch7=[11101] 0,39 NIE
ch8=[01010] 0,76 NIE
Слайд 34
Algorytm genetyczny – przykład 1
4. Operacje genetyczne -
mutacja
Po operacji mutacji otrzymujemy następującą populację potomków
o fenotypach
ch1=[10001] ch1*=17
ch2=[10010] ch2*=18
ch3=[00100] ch3*=4
ch4=[10011] ch4*=19
ch5=[10010] ch5*=18
ch6=[10010] ch6*=18
ch7=[11010] ch7*=26
ch8=[01101] ch8*=13
Слайд 35
Algorytm genetyczny – przykład 1
5. Obliczamy funkcje przystosowania
dla nowej populacji
F(ch1)=2•ch1*+1=35
F(ch2)=37
F(ch3)=9
F(ch4)=39
F(ch5)=37
F(ch6)=37
F(ch7)=59
F(ch8)=27
Suma=280
Слайд 36
Strategie ewolucyjne
Tak jak algorytmy genetyczne operują na populacjach
potencjalnych rozwiązań i korzystają z zasad selekcji i przetwarzania
osobników najlepiej przystosowanych.
Działają na wektorach liczb zmiennoprzecinkowych a nie binarnych.
W procedurze selekcji tworzona jest tymczasowa populacja której wielkość różni się od populacji rodzicielskiej. Kolejna generacja osobników powstaje przez wybór najlepszych osobników.
Osobniki rodzicielskie wybierane są bez powtórzeń.
Najpierw osobniki podlegają krzyżowaniu i mutacji a potem następuje selekcja z powstałej populacji tymczasowej. Wybiera się tyle najlepszych osobników ile było rodziców.
Parametry takie jak prawdopodobieństwo krzyżowania i mutacji mogą się zmieniać w czasie trwania algorytmu.
Слайд 37
Strategia ewolucyjna (1+1)
Przetwarzany jest jeden chromosom bazowy x,
którego wartość początkowa jest ustalana losowo
W każdej generacji w
wyniku mutacji powstaje nowy osobnik y
Po porównaniu funkcji przystosowania F(x) i F(y) wybierany jest lepszy osobnik, który zostaje nowym osobnikiem bazowym x
W algorytmie nie występuje operator krzyżowania
Chromosom y powstaje przez dodanie do każdego genu chromosomu x pewnej liczby losowej generowanej zgodnie z rozkładem normalnym.
Слайд 38
Strategia ewolucyjna (μ+λ)
Algorytm rozpoczyna się od wylosowania początkowej
populacji rodzicielskiej P składającej się z μ osobników
Tworzy się
populacja tymczasowa T zawierająca λ osobników (λ≥ μ).
Populacja ta powstaje poprzez losowanie λ osobników z populacji P (losowanie ze zwracaniem)
Osobniki z populacji T podlegają krzyżowaniu i mutacji i w ten sposób powstaje populacja potomna O zawierająca λ osobników
Z obu populacji P∪O wybieramy μ najlepszych osobników, które tworzą nową populację rodzicielską P.












![Algorytmy ewolucyjne Algorytm genetyczny – przykład 1Szukanie maksimum funkcji y=2x+1 dla x∈[0,31]x – parametr](/img/tmb/14/1397243/602fef101c16ec739292d686b93b2f0b-720x.jpg)