Слайд 2
существуют среды, используемые при решении разных задач:
генетических
исследований, при обработке штаммов мутагенами;
селекции мутантов — полноценные и
селективные среды;
длительного хранения и пересевов штаммов микроорганизмов;
оптимизации продуктивности штамма в колбах;
для инокулята и посевного материала (в том числе вегетативного и спорового);
оптимизации продуктивности в ферментерах производственного масштаба.
Слайд 3
Выбор критерия оптимизации (применительно к средам в колбах)
количество
целевого продукта;
производительность по целевому продукту;
выход целевого продукта по субстрату;
минимизация
стоимости среды для получения единицы целевого продукта.
Слайд 4
Выбор исходных компонентов среды
При подборе сред в
первую очередь следует обратить внимание на химический состав биомассы
микроорганизмов и на химический состав внеклеточного продукта, если он является целевым.
Основные компоненты среды — источники углерода (и одновременно энергии), азота, фосфора, серы, микроэлементов, ростовых факторов и витаминов для начала роста биомассы.
Слайд 5
Определение соотношения компонентов среды
. Рецептуры сред для
промышленных штаммов охраняются как большой секрет, и многие микробиологи
занимаются их подбором.
Когда в составе среды только один компонент не изучен и необходимо определить его оптимальную концентрацию, достаточно провести серию опытов, в которых исследуемый компонент будет находиться в разных концентрациях.
Проведения опытов с 4—5 разными концентрациями (уровнями) компонента достаточно, чтобы получить представление о характере его влияния.
Слайд 6
ТРАДИЦИОННЫЕ МЕТОДЫ ИЗУЧЕНИЯ МНОГОФАКТОРНЫХ ЗАВИСИМОСТЕЙ
Необходимо построить поверхность отклика,
напоминающую топографическую карту. На этой карте на двух осях
координат отложена величина факторов S1 и S2, а в самом графике проведены контурные линии равного уровня, соответствующие одинаковому выходу Р — параметру оптимизации.
Слайд 7
для построения «топографической карты» нужно «изрешетить» всю площадь
в изучаемом диапазоне S1 и S2 опытами.
Слайд 8
Отдельное изучение каждого фактора.
при подборе сред микробиологи
применяют исходный «фон» — определенное соотношение уровней факторов (концентраций
компонентов) в среде. На этом «фоне» ставят однофакторные эксперименты по каждому из n факторов и получают столько же кривых, сколько изучают факторов.
Слайд 9
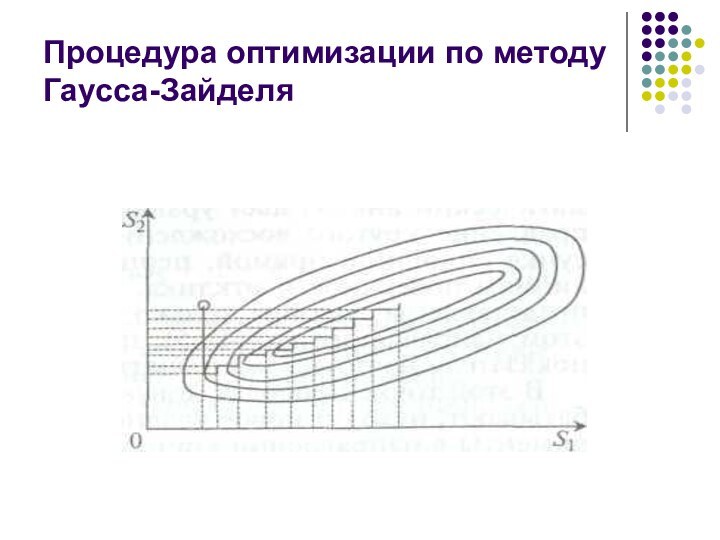
Метод Гаусса — Зайделя
этот метод называют «последовательным
изучением каждого фактора». Здесь частные зависимости Р (S1), P
(S2), P (Sn) находят не сразу на одном и том же «фоне», а по очереди. Сначала определяют Р (Si), анализируют эту зависимость, находят частный оптимум для фактора Si, затем меняют «фон», установив в нем значение Si, равное этому частному оптимуму.
Слайд 10
Недостатки метода:
метод Гаусса — Зайделя следует повторять пока
частные оптимумы по отдельным факторам не перестанут изменяться от
одной серии опытов к другой.
метод имеет и еще один недостаток по сравнению с предыдущими: необходимо поочередное выполнение серий экспериментов, так как изменение «фона» требует анализа результатов каждой серии.
Слайд 11
Процедура оптимизации по методу Гаусса-Зайделя
Слайд 12
МЕТОД БОКСА — УИЛСОНА
По этому методу вблизи
исходной точки («фона») ставится специальным образом спланированная небольшая серия
опытов, в которой одновременно варьируются все изучаемые факторы, каждый на 2 уровнях (верхнем и нижнем).
Результаты этих опытов математически обрабатывают для получения приближенного математического описания процесса в этой локальной области. Для двух уровней варьирования факторов находят линейное уравнение (уравнением регрессии), величина факторов входит в первой степени.
Слайд 13
Процедура оптимизации по методу Бокса-Уилсона
Слайд 14
Исследовательская серия опытов
сначала ставится небольшая серия опытов
на двух уровнях — верхнем и нижнем. Для каждого
фактора эти уровни отличаются от основного уровня (исходного уровня «фона») на одну и ту же величину.
Эта величина называется интервалом варьирования и обозначается X. Для разных факторов величина λ. может быть разной.
Слайд 15
Для чего ставится исследовательская серия опытов?
Чтобы получить
линейное уравнение, связывающее выходной параметр оптимизации Р с влияющими
факторами:
Слайд 16
для упрощения расчетов по методу Бокса—Уилсона опыты ставят
не при произвольным образом измененных значениях уровней разных факторов,
а по так называемым ортогональным матрицам
В этих матрицах (перечне вариантов, взятых в данной исследовательской серии опытов) из всех возможных 2n вариантов опытов, когда n факторов варьируется на 2 уровнях, выбирают небольшое количество вариантов со следующими свойствами
Слайд 17
Свойства матрицы:
1. в каждой серии количество вариантов опытов
с верхним уровнем каждого фактора равно количеству вариантов с
нижним уровнем того же фактора;
2. верхний уровень любого фактора сочетается одинаковое число раз и с верхними, и с нижними уровнями всех остальных факторов, он как бы проверяется на усредненном фоне, в котором влияние уровней остальных факторов нивелируется. Это же положение справедливо и для нижних уровней.
Слайд 18
Планы ортогональных матриц разработаны для различного числа факторов
n и могут включать разное число вариантов планирования. Практически
в исследовательских сериях стараются уменьшить число вариантов опытов. Для этого целесообразно выбрать ближайшую матрицу с числом вариантов большим, чем (n + 2).
Слайд 19
Планы экспериментов имеются в различных справочниках и руководствах.
Слайд 20
Матрица планирования для 6 факторов на 2 уровнях
состоящая из 8 экспериментов, может быть использована также для
3 факторов (это — полный факторный эксперимент), для 4 и для 5 факторов (вычеркивая за ненадобностью 1, 2 или 3 столбца из этой матрицы).
Слайд 21
После выбора матрицы планирования, числа варьируемых факторов и
интервалов планирования можно переходить от условных обозначений матриц, выраженных
чередованием знаков (-) и (+), к их физическому наполнению реальными значениями концентраций компонентов среды, которые предстоит проверять в опытах при оптимизации состава среды. Все результаты удобно записывать в сводную таблицу.
Слайд 22
Пример оптимизации 4-х компонентной среды по методу Бокса-Уилсона
Слайд 23
Продолжение таблицы
оптимизация 4-х компонентной среды по методу
Бокса-Уилсона
Слайд 24
оптимизация среды по методу Бокса-Уилсона
После выбора матрицы планирования,
числа варьируемых факторов и интервалов планирования можно переходить от
условных обозначений матриц, выраженных чередованием знаков (-) и (+), к их физическому наполнению реальными значениями концентраций компонентов среды, которые предстоит проверять в опытах при оптимизации состава среды.
Слайд 25
МАТЕМАТИЧЕСКИЕ ПРОЦЕДУРЫ В МЕТОДЕ БОКСА—УИЛСОНА
основной уровень («фон»), интервалы
варьирования, минимальный и максимальный уровни фактора, при которых исследователь
допускает протекание процесса, определяются интуицией.
необходимо найти физические значения верхнего и нижнего уровней факторов.
Для этого к основному уровню нужно прибавить интервал варьирования — для верхнего уровня или вычесть его — для нижнего уровня.
Слайд 26
МАТЕМАТИЧЕСКИЕ ПРОЦЕДУРЫ В МЕТОДЕ БОКСА—УИЛСОНА
кроме варьируемых факторов в
составе среды могут быть факторы, значение которых одинаково для
всех вариантов среды.
надо не забывать при приготовлении сред добавлять и эти постоянные для всех сред компоненты, хотя в матрице планирования они и не указаны.
Слайд 27
Постановка эксперимента
В микробиологических исследованиях принято для надежности
повторять опыты и не по одному разу. Это касается
и опытов с планированием эксперимента при подборе сред.
в данных опытах есть одна особенность:
- не интересны конкретные цифры для каждой отдельной среды:
- вся серия в целом служит одной задаче: найти более точно описание всей области эксперимента уравнением, а с ним — и более точное направление движения к оптимуму;
- каждая точка матрицы помогает другой и они дают совокупный результат.
Это позволяет снизить требования к повторению опытов.
Слайд 28
Расчет коэффициентов уравнения регрессии
Свободный член уравнения bо
находится как среднее из значений Р для всех N
вариантов матрицы:
где Р u — среднее значение величины Р для всех повторений для u-го варианта матрицы.
Слайд 29
Коэффициент регрессии i-го фактора определяется как разность сумм
выходов Ри, в которых фактор Si, находился со знаком
(+), и выходов Ри, где фактор Si, находился со знаком
(-), деленная на число вариантов в матрице планирования N:
Слайд 30
Если принять кодированные значения факторов Xi т.е. Siu,
как (+1) для верхнего уровня и (—1) для нижнего,
то получаем:
Слайд 31
Например, для фактора S2 в таблице коэффициент регрессии
вычисляют следующим образом:
Слайд 32
Рассчитанные таким образом коэффициенты имеют разные знаки. Знак
(+) означает, что при увеличении данного фактора происходит возрастание
параметра оптимизации Р, знак (-) - наоборот, уменьшение Р.
Чем больше коэффициент регрессии, тем больше он влияет на результат процесса.
Слайд 33
На основе коэффициентов регрессии можно записать уравнение
Чтобы
перейти к натуральным переменным, нужно подставить выражение для кодированных
факторов:
где Si и Soi — натуральные значения уровня i-го фактора в данном опыте и основного уровня этого фактора; λ i — интервал варьирования i-го фактора в натуральных величинах
Слайд 34
Определение запаса для движения в направлении крутого восхождения
При определении программы крутого восхождения от основного уровня необходимо
знать для каждого фактора запас ∆i,- в сторону движения [для коэффициентов регрессии со знаком (+) - в сторону увеличения, со знаком (-) - в сторону уменьшения]:
Слайд 35
Определение вспомогательного показателя «критичность».
Этот показатель представляет собой
модуль отношения запаса ∆i, и произведения biλi,- и физически
выражает в сравнительном аспекте, сколько сможет уместиться в «запасе» шагов в направлении крутого восхождения для разных факторов с учетом их степени влияния на результат процесса.
Чем ниже значение показателя критичности для фактора, тем меньшее (по сравнению с другими) число шагов уместится в «запасе» для этого фактора.
Слайд 36
Выбор шага крутого восхождения
Обычно крутое восхождение проводится
путем равномерного пошагового приращения в каждом последующем опыте величины
уровня фактора.
При этом для одного из факторов — наиболее критичного — величина приращения (шага) выбирается, а для всех остальных — рассчитывается так, чтобы их значения были пропорциональны произведениям biλi.
Слайд 37
Выбор шага крутого восхождения
Обычно выбирают относительно немного шагов
в направлении крутого восхождения: 5—8, не более.
По наиболее
критичному фактору выбранное количество шагов т позволяет определить величину шага ∆Si
Слайд 38
Выбор шага крутого восхождения
Если величина базового шага равна
0,5,то пропорционально произведениям biλi,- найдем величину шага ∆Si, для
факторов Si:
Слайд 39
Для фактора проставлен прочерк.
Значит по результатам анализа
установлено, что данный фактор не оказывает существенного влияния на
результат процесса, а потому его значение нет смысла менять.
Как определить, что тот или иной фактор является значимым или незначимым?
Для этого в планировании эксперимента предусмотрена специальная процедура.
Слайд 40
СТАТИСТИЧЕСКАЯ ОЦЕНКА РЕЗУЛЬТАТОВ
В биологических процессах результат процесса
обычно неоднозначен.
Существует какой-то уровень колебаний, возможных по случайным
причинам.
Природа этих колебаний (источников неоднородности) может быть различной. Это ошибки в определении результата, и различия в значении факторов при проведении эксперимента, и неточности приготовления сред, и вообще присущая биологическим объектам неоднородность.
Слайд 41
коэффициенты регрессии определяют по значениям выходного показателя, для
них есть уровень случайных изменений, который находят с помощью
статистической обработки.
Уровень воспроизводимости процесса характеризуется дисперсией.
Для определения дисперсии воспроизводимости существуют два способа.
Слайд 42
Первый способ— многократное повторение опытов для одного и
того же варианта (среды).
В этом случае имеем ряд значений
Р, их количество обозначим γ, оно не должно быть меньше 8—10.
Нужно найти среднюю величину Р для всех γ опытов, все отклонения от среднего (Р-Р), квадраты этих отклонений и сумму квадратов ∑(Pj—P)2 для всех γ повторений.
Слайд 43
Дисперсию воспроизводимости определяют по формуле:
Это не среднеквадратичное
отклонение, а дисперсия воспроизводимости каждого отдельного измерения.
Слайд 44
Если выполнить несколько серий опытов на одной и
той же среде (в каждой серии число опытов γ),
затем для каждой серии рассчитать свою среднюю величину Р , и посмотреть, какова будет дисперсия воспроизводимости для этих средних значений, то получим:
Слайд 45
Второй способ— расчет дисперсии процесса по данным повторных
экспериментов матрицы планирования.
Он более удобен при планировании эксперимента, так
как повторения в каждом варианте матрицы предусмотрены. Если γ — число повторений в каждом варианте среды, а
N — общее число вариантов сред в матрице, то дисперсию воспроизводимости единичного значения находят по формуле
Слайд 46
Надежность вычисления дисперсии воспроизводимости определяется количеством «лишних» опытов,
необходимых для нахождения дисперсии.
Количество «лишних» опытов называют числом степеней
свободы f. Для первого способа оно равно (γ - 1), для второго — N(γ - 1). Эта величина является важным статистическим показателем.
Слайд 47
для надежного определения дисперсии воспроизводимости процесса число степеней
свободы f должно быть не менее 5—8.
Чем больше
дисперсия, тем хуже воспроизводимость процесса.
Корень квадратный из дисперсии воспроизводимости процесса называют стандартным отклонением, или стандартной ошибкой.
Слайд 48
Определение значимости коэффициентов регрессии.
Уровень возможных случайных колебаний
коэффициентов регрессии называется доверительным интервалом, обозначается буквой ε и
его вычисляют по формуле:
Слайд 49
В этой формуле появляется новый коэффициент t —
критерий Стьюдента, определяемый по таблицам.
Для надежности оценки до
95% критерий Стьюдента зависит только от числа степеней свободы f при которых находим дисперсию воспроизводимости.
Слайд 50
значения критерия Стьюдента для наиболее часто встречающихся значений
f при Р = 0,95:
вначале критерий t резко
уменьшается с возрастанием f, а затем его значение стабилизируется.
Слайд 51
Доверительный интервал ε имеет одно и то же
значение для всех коэффициентов bi (в кодированном виде).
Сравнение
коэффициента регрессии с доверительным интервалом и позволяет сделать вывод о его значимости.
Все коэффициенты bi , значения которых ниже доверительного интервала, незначимы. Их можно считать нулевыми.
Если величина коэффициента больше ε, он значим. Отрицательные коэффициенты регрессии тоже значимы, если они по модулю превосходят ε.
Слайд 52
Незначимость коэффициентов может быть вызвана различными причинами:
1. взяты
слишком малые интервалы варьирования фактора;
2. плохая воспроизводимость процесса —
все различия в выходе нивелируются ошибкой опыта;
3. данный фактор находится на уровне, близком к оптимальному;
4. данный фактор не влияет на процесс вообще, по крайней мере в изученной области.
Слайд 53
Адекватность математического описания процесса
Кроме оценки значимости коэффициентов
в процедуре статистического анализа предусмотрена оценка адекватности полученного математического
описания в целом.
Для этого сначала находят дисперсию адекватности, которая характеризует отклонение рассчитанных по уравнению значений выходного показателя Р от найденного в эксперименте Р.
Слайд 54
для варианта 6 величину Р можно определить так
Слайд 55
Дисперсия адекватности определяется по формуле
где n — число
факторов в уравнении; N — число вариантов опытов (условий),
по которым определяется дисперсия адекватности; и — номер варианта среды, к которому относятся Р и Р.
Слайд 56
Знаменатель этой дроби представляет собой число степеней свободы
fа дисперсии адекватности:
fa = N - n
- 1;
т.е. количество «лишних» опытов, имеющихся в плане сверх минимально необходимых (n + 1) — по числу коэффициентов в уравнении.
Степень адекватности математического описания оценивают по критерию Фишера F, который вычисляют по формуле:
Слайд 57
Чтобы найти адекватность уравнения, необходимо критерий Фишера сравнить
с табличным FT, имеющимся в справочниках по статистике, также
для надежности оценки 95%.
Уравнение считается адекватным, если F < FT, и наоборот.
FT в таблице определяют исходя из двух видов степеней свободы: fp — для воспроизводимости самого процесса и fa — для дисперсии адекватности.
Слайд 58
Расчет программы крутого восхождения
Для данного примера рассчитывают
условия для 6 шагов крутого восхождения, т. е. 6
новых сред.
На каждом шаге к предыдущему уровню фактора прибавляется или от него отнимается рассчитанное значение шага.
По наиболее критичному фактору последний шаг будет совпадать с максимальным или минимальным его уровнем, по другим факторам — несколько не доходить до них.
Составляют 6 сред крутого восхождения и воспроизводят процесс с этими рассчитанными средами. Для факторов с отрицательным значением коэффициента регрессии при каждом шаге отнимается, а не прибавляется величина рассчитанного ∆S;.
Слайд 59
Анализ результатов крутого восхождения
сначала нужно все значения
уровней факторов пересчитать в кодированные.
затем рассчитать величину Р аналогично
тому, как это делалось для опытов в исследовательской матрице, подставив вместо кодированных значений Si (-1) и (+1) значения, вычисленные по формуле:
Слайд 60
В колонке рядом с расчетными данными указать экспериментальные.
Часто столь высоких значений выхода, как ожидали, не получают.
Рост выходного показателя может идти не все время — после 4-го шага ( 12-го опыта) начинается даже падение выхода.
Значит линейное приближение недостаточно. Но направление движения к оптимуму найдено.
Далее нужно поставить новую матрицу планирования с центром в новой точке и наметить программу крутого восхождения.
Слайд 61
расчет по этому методу необходимо повторять до тех
пор, пока линейное уравнение не станет неадекватным. В этом
случае надо использовать другие методы, описывающие процесс уже уравнением второго порядка:
Слайд 62
МНОГОУРОВНЕВЫЕ ПЛАНЫ ЭКСПЕРИМЕНТА
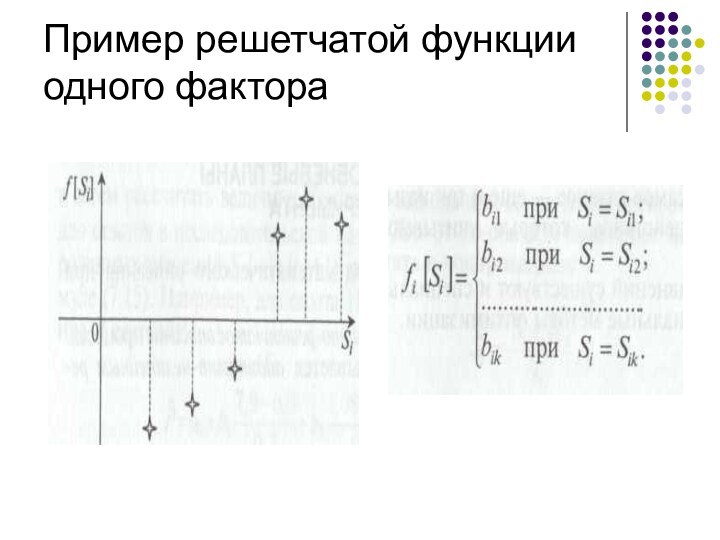
методом является аддитивно-решетчатое описание процесса.
В
этом случае объект описывается аддитивно-нелинейным решетчатым уравнением:
Слайд 63
Аддитивное — значит состоящее из суммы членов, каждый
из которых зависит только от одного из факторов.
Принятое
в методе Бокса—Уилсона линейное уравнение регрессии было аддитивным, только значения каждой функции были линейными:
Здесь функции могут быть и нелинейными
(
Слайд 64
Пример решетчатой функции одного фактора
Слайд 65
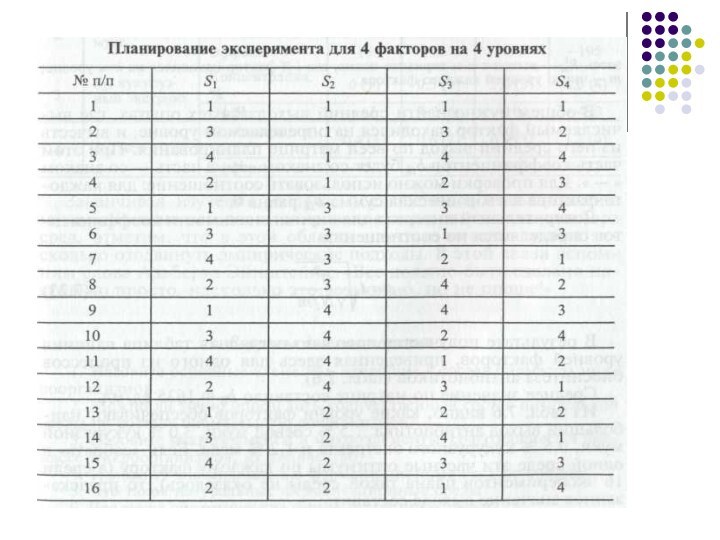
Чтобы получить зависимости с наименьшим числом опытов и
упростить вычисления, целесообразно использовать ортогональные матрицы планирования уже на
3, 4, 5 уровнях в соответствии с выбранной разбивкой рабочего диапазона для всех факторов.
Ортогональность матриц предполагает, что каждый уровень любого фактора сочетается одинаковое число раз со всеми уровнями остальных факторов.
Слайд 66
На практике такие схемы планирования эксперимента называют схемами
ортогональных латинских прямоугольников (или квадратов, если число факторов равно
числу уровней каждого фактора).
Есть удобные для практики схемы планирования — 3x3, 4x4, 5 х 5, 8 х 4, 9 х 3. Первая цифра обозначает число факторов, а вторая — число уровней каждого фактора.
Слайд 68
Величина эффектов решетчатого описания (bik) и значение bо
рассчитываются почти так же просто, как в методе Бокса—
Уилсона:
Pkiu— выход в и-м варианте плана, где i-й фактор находился на k-м уровне; т — число уровней каждого фактора
Слайд 69
нужно найти средний выход Р в тех опытах,
где вычисляемый фактор находится на определяемом уровне,
вычесть из него средний выход по всей матрице планирования. При этом часть коэффициентов bik будет со знаком «+», а часть — со знаком «-».
Для проверки можно использовать соотношение: для каждого фактора алгебраическая сумма bik. равна 0.
Доверительный интервал для оценки значимости коэффициентов определяется по соотношению
Слайд 70
Итоги расчетов величины эффектов аддитивно-решетчатого описания
Слайд 71
Адекватность аддитивно-решетчатого описания проверяют аналогично методу Бокса—Уилсона. При
нахождении дисперсии адекватности число степеней свободы fa принимают fа
= N- п (т - 1) - 1.
«Все должно быть сделано настолько просто, насколько это возможно, но не проще!»
Альберт Эйнштейн