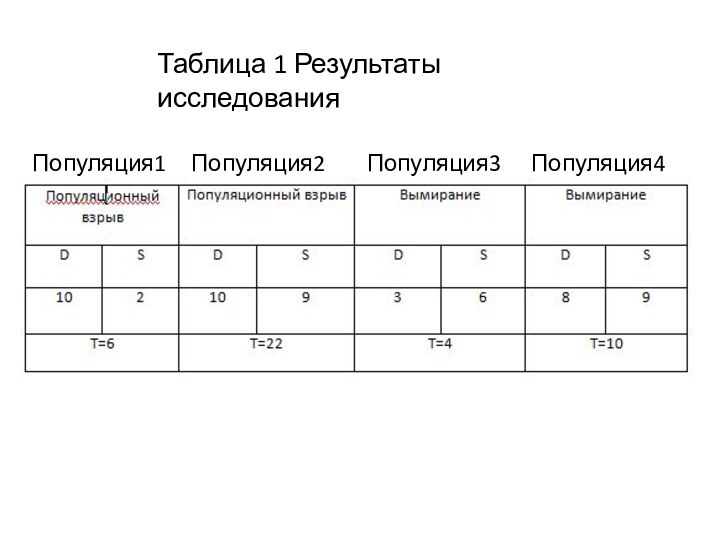
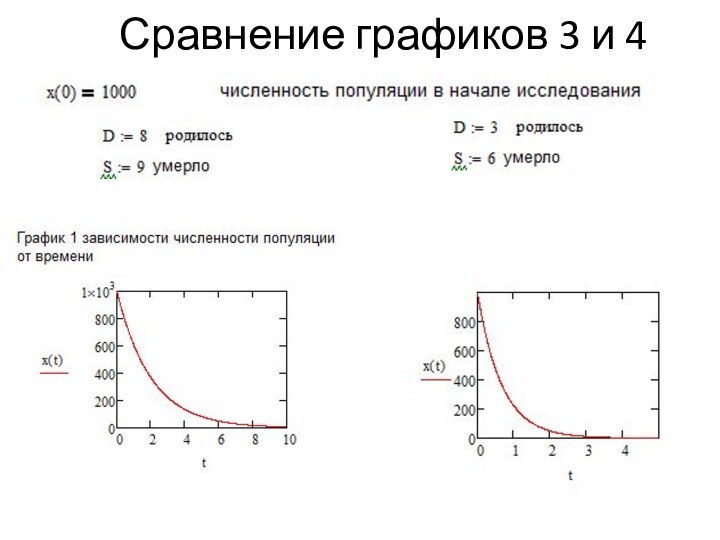
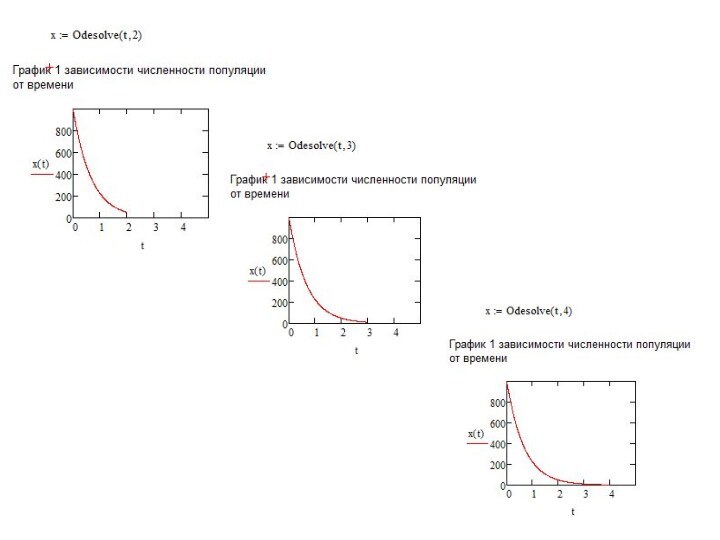
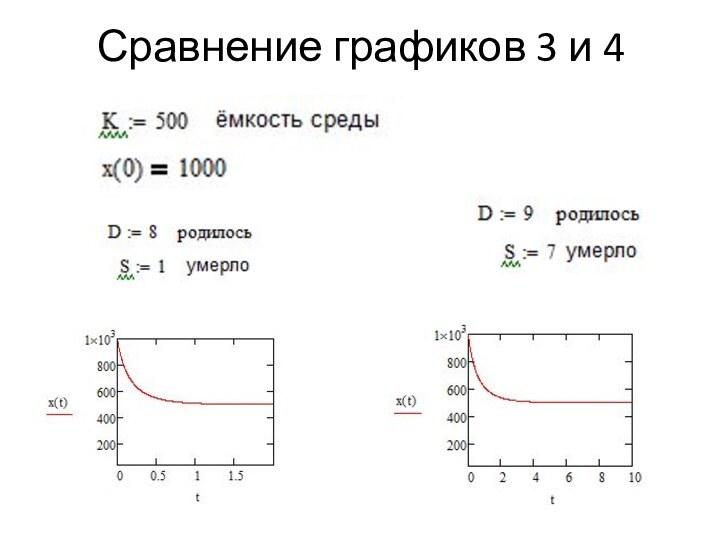
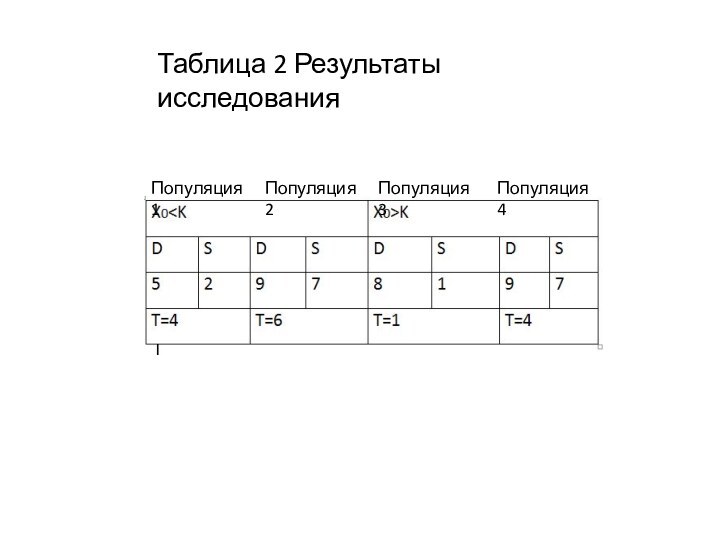
ростом
Условия
Предположим, что:
Рассматривается популяция организмов, которые размножаются
непрерывно, причем поколения
широко перекрываются и особи разных генераций и возрастов могут встречаться одновременно. процессы иммиграции и эмиграции уравновешивают друг друга;
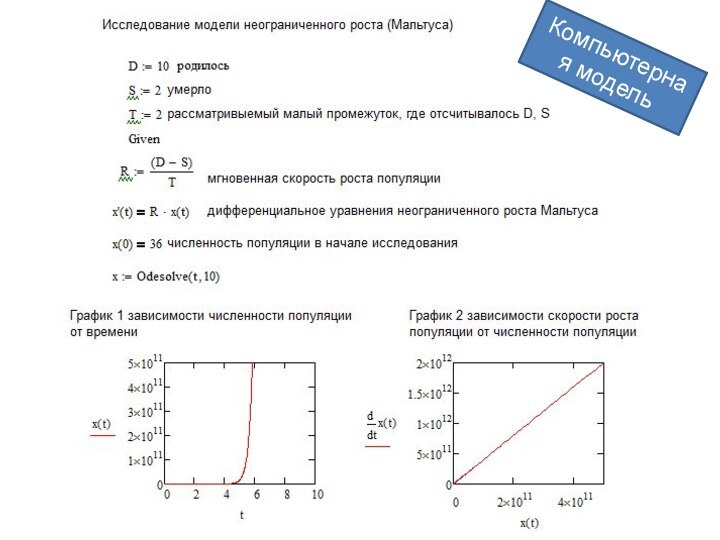
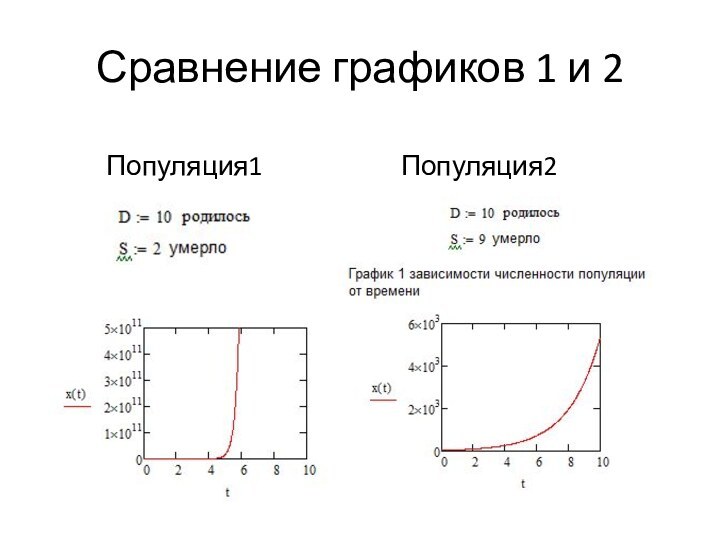
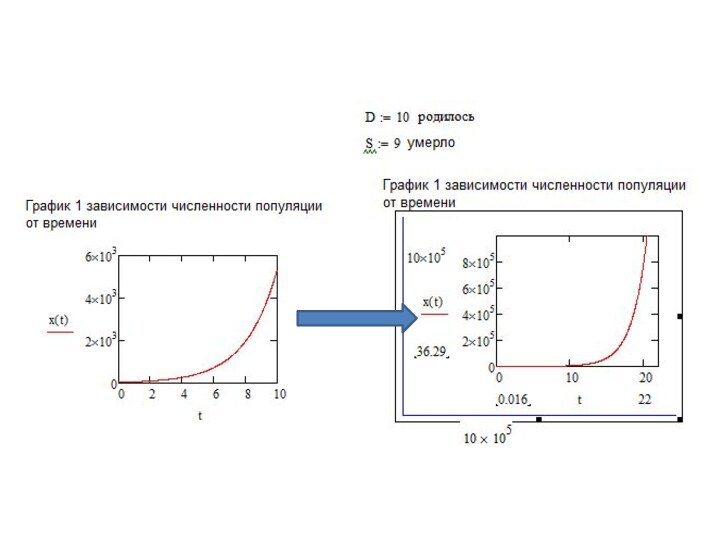
лишь рождение D и гибель S особей влияют на плотность популяции;
все особи идентичны друг другу, в особенности в отношении их способности к размножению и вероятности гибели;
мы можем игнорировать все сложности связанные с обоеполым размножением,
ресурсы среды бесконечны и поэтому только врожденные способности особей к размножению и их смертность влияют на величину популяции.