Слайд 2
Термодинамика (от греч. Therme — тепло + Dynamis — сила) — раздел
физики, изучающий соотношения и превращения теплоты и других форм
энергии. Термодинамика рассматривает общие закономерности превращения энергии в форме тепла и работы между телами.
Термодинамика исторически возникла как эмпирическая наука об основных способах преобразования внутренней энергии тел для совершения механической работы
Слайд 3
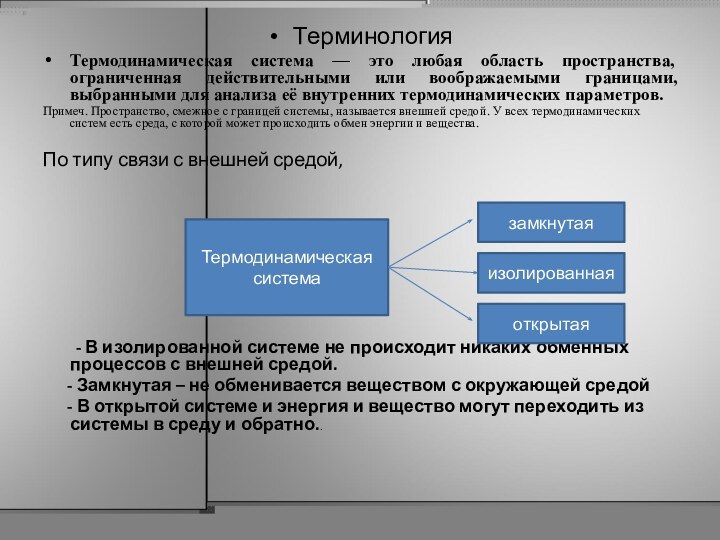
Терминология
Термодинамическая система — это любая область пространства, ограниченная
действительными или воображаемыми границами, выбранными для анализа её внутренних
термодинамических параметров.
Примеч. Пространство, смежное с границей системы, называется внешней средой. У всех термодинамических систем есть среда, с которой может происходить обмен энергии и вещества.
По типу связи с внешней средой,
- В изолированной системе не происходит никаких обменных процессов с внешней средой.
- Замкнутая – не обменивается веществом с окружающей средой
- В открытой системе и энергия и вещество могут переходить из системы в среду и обратно..
Термодинамическая система
замкнутая
открытая
изолированная
Слайд 4
Состояние термодинамической системы определяется физическими свойствами вещества.
Температура, давление,
объем, внутренняя энергия, энтальпия и энтропия — это термодинамические
величины, определяющие те или иные интегральные параметры системы.
(!) Данные параметры строго определяются лишь для систем, находящихся в состоянии термодинамического равновесия.
Слайд 5
ЭНЕРГИЯ (от греч. energeia -
действие - деятельность), общая количественная мера различных форм движения
материи.
Различным физическим процессам соответствует тот или иной вид энергии: механическая, тепловая, электромагнитная, гравитационная, ядерная и т. д.
(!) Вследствие существования закона сохранения энергии понятие энергии связывает воедино все явления природы.
РАБОТА - форма обмена энергией (наряду с теплотой) термодинамической системы (физического тела) с окружающими телами;
-количественная характеристика преобразования энергии в физических процессах, зависит от вида процесса; работа системы положительна, если она отдает энергию, и отрицательна, если получает.
Слайд 6
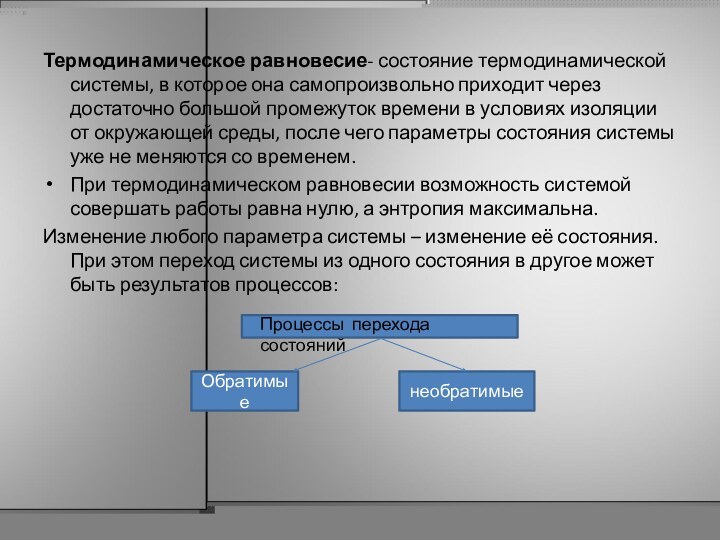
Термодинамическое равновесие- состояние термодинамической системы, в которое она
самопроизвольно приходит через достаточно большой промежуток времени в условиях
изоляции от окружающей среды, после чего параметры состояния системы уже не меняются со временем.
При термодинамическом равновесии возможность системой совершать работы равна нулю, а энтропия максимальна.
Изменение любого параметра системы – изменение её состояния. При этом переход системы из одного состояния в другое может быть результатов процессов:
Обратимые
необратимые
Процессы перехода состояний
Слайд 7
Обратимые и необратимые термодинамические
процессы
Если в результате

процесса состояние системы не изменяется, то такой процесс называется
обратимым
И наоборот, если в результате процесса система не вернется в исходное состояние, то такой процесс называется необратимым.
Обратимый процесс-процесс перехода термодинамической системы из одного состояния в другое, допускающий возможность возвращения её в первоначальное состояние через ту же последовательность промежуточных состояний, но проходимых в обратном порядке. Для того чтобы процесс был обратимым, он должен быть столь медленным, чтобы его можно было рассматривать как непрерывный ряд равновесных состояний, т. е. он должен быть медленным по сравнению с процессами установления равновесия термодинамического в данной системе. Строго говоря, обратимый процесс характеризуется бесконечно медленным изменением термодинамических параметров (плотности, давления, температуры и др.), определяющих равновесие системы. Такие процессы называются также квазистатическими или квазиравновесными. Обратимость квазиравновесного процесса следует из того, что его любое промежуточное состояние есть состояние термодинамического равновесия и поэтому оно не чувствительно к тому, идёт ли процесс в прямом или обратном направлении.
Слайд 8
Необратимые т/д процессы – называют такие процессы, которые
могут самопроизвольно протекать только в одном определённом направлении. К
ним относятся: процессы диффузии, теплопроводности, термодиффузии, вязкого течения, расширения газа в пустоту и т.п. Все они являются неравновесными процессами.
В замкнутых системах необратимые процессы сопровождаются возрастанием энтропии.
В открытых системах (которые могут обмениваться энергией или веществом с окружающей средой) при необратимых процессах энтропия может оставаться постоянной или даже убывать за счёт обмена энтропией с внешней средой.
Однако здесь, во всех случаях остаётся положительным производство энтропии, т. е. её возрастание в системе за единицу времени.
В природе, большинство процессов являются необратимыми, а обратимые могут совершаться лишь в состоянии термодинамического равновесия.
Слайд 9
Диссипация энергии
Диссипация энергии, - у физических систем переход
части энергии упорядоченного процесса (например, электрической энергии) в энергию
неупорядоченного процесса — в конечном счёте в тепловую (например, в джоулево тепло). У механических систем переход части её механической энергии в др. формы (например, в теплоту) происходит за счёт наличия сил сопротивления; в атмосфере — переход части кинетической энергии ветра в теплоту под воздействием внутреннего трения.
Слайд 10
Внутренняя энергия
Внутренняя энергия - энергия тела, зависящая только
от его внутреннего состояния. Понятие В. э. объединяет все
виды энергии тела, за исключением энергии его движения как целого и потенциальной энергии, которой тело может обладать, если оно находится в поле каких-нибудь сил.
Слайд 11
Биологические системы –открытые системы, в них постоянно происходит
процесс обмена энергией с внешней средой.
Внутренние метаболические процессы
также сопровождаются превращениями одних форм энергии в другие.
Например:
- трансформация энергии кванта света в энергию электронного возбуждения молекул пигментов, а затем в энергию химических связей восстановленных соединений в фотосинтезе.
-преобразование энергии электрохимического трансмембранного потенциала в энергию АТФ в биологических мембранах.
Слайд 12
Механизмы трансформации энергии в биоструктурах связаны с конформационными
превращениями особых макромолекулярных комплексов, таких, как реакционные центры фотосинтеза,
Н-АТФаза хлоропластов и митохондрий, бактериородопсин. Однако помимо выяснения детального характера происходящих здесь процессов особый интерес представляют общие характеристики эффективности преобразования энергии в таких макромолекулярных машинах.
На эти вопросы призвана ответить термодинамика биологических процессов - один из разделов теоретической биофизики.
Слайд 13
ТЕРМОДИНАМИКА НЕОБРАТИМЫХ ПРОЦЕССОВ В БИОЛОГИЧЕСКИХ СИСТЕМАХ ВБЛИЗИ РАВНОВЕСИЯ
В
классической термодинамике рассматриваются главным образом равновесные состояния системы, в
которых параметры не изменяются во времени.
Однако в открытых системах реакции и соответствующие энергетические превращения происходят постоянно, и поэтому здесь необходимо знать скорости трансформации энергии в каждый момент времени. Это значит, что в энергетических расчетах надо учитывать и фактор времени. Для этого необходимо каким-то образом сочетать термодинамический и кинетический подходы в описании свойств открытой системы.
Слайд 14
Первый закон термодинамики
«Изменение внутренней энергии (dU)
тела (системы) при переходе из одного состояния в другое
равно сумме совершенной над телом работы (А’) и полученного им количества теплоты (dQ)»
Примечание: здесь учитываются две формы передачи энергии – работа и теплота.
В случае если сама система совершает работу над внешними телами , т.е.
А= -А’ , то имеем:
dQ = dU + dA, (1)
Согласно первому закону, количество теплоты dQ, поглощенное системой из внешней среды, идет на увеличение ее внутренней энергии dU и совершение общей работы dA, которая включает работу против сил внешнего давления P по изменению объема dV системы и максимальную полезную работу dAmax ,сопровождающую химические превращения:
Слайд 15
где работа (А)
dА =
pdV + dAmax (2)
Или
dQ = dU +
pdV + dAmax .
Опытная проверка первого закона применительно к биосистемам, проводилась в специальных калориметрах, где измерялась теплота, выделенная организмом в процессах метаболизма, при испарениях, а также вместе с продуктами выделения. Оказалось, что выделенная организмом теплота полностью соответствует энергии, поглощенной вместе с питательными веществами.
Справедливость первого закона означает, что сам по себе организм не является независимым источником какой-либо новой энергии.
Виды работы совершаемой
в живых организмах:
1. химическая –синтез органических веществ (ВМС из низкомолекулярных и т.п.)
2. механическая – перемещение частей и органов против механических сил (работа мышц).
3. осмотическая – перенос веществ через био - барьеры (мембраны)
4. электрическая –работа по переносу заряженных частиц в электрическом поле, создание биопотенциалов и т.п.
Первичным источником энергии в организме является химическая энергия пищевых веществ.
Слайд 17
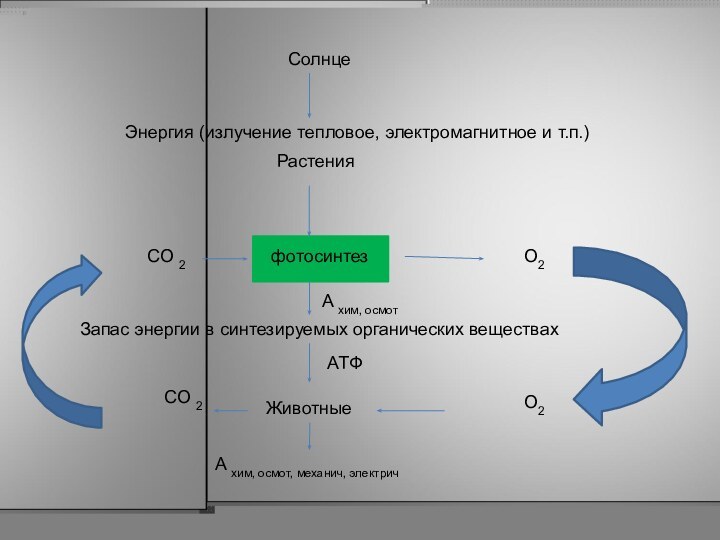
Солнце
Энергия (излучение тепловое, электромагнитное и т.п.)
Растения
фотосинтез
СО 2
Запас энергии в синтезируемых органических веществах
O2
A хим, осмот
Животные
O2
СО
2
АТФ
A хим, осмот, механич, электрич
Слайд 18
АТФ + Н2O
АДФ
+
Н3 PO4
+
Q (8.5 ккал)
Q
(теплота)
первичная (обмен веществ)
вторичная (затрачивается на производство работы)
Процессы происходящие
в живом организме являются, с точки зрения
ТД, необратимыми (протекают с переходом части энергии в тепло)
Слайд 19
Энтальпия. Закон Гесса
Образование теплоты у гомойотермных животных в
покое:
50 % в органах брюшной полости
20 % в скелетных
мышцах
10 % при работе органов дыхания и кровообращения
Теплота организма:
Основная (первичная) – рассеивание Е в ходе реакциий диссимиляции (во основе б-х процессы необратимого типа)
Особенности
выделяется сразу после поглощения О2 (или продуктов питания)
не зависит от совершения А организмом
расходуется на нагрев организма и рассеивается в окружающую среду
2. Активная (вторичная)-выделяется при реализации Е макроэргов в ходе обменных реакций, связанна с выполнением А
Слайд 20
! При физиологических условиях существует равенство между первичной
и вторичной теплотой!
При патологии – воспаление-происходит разобщение окислительного фосфорилирования,
увеличивается доля первичной теплоты , что сопровождается возрастанием температуры организма.
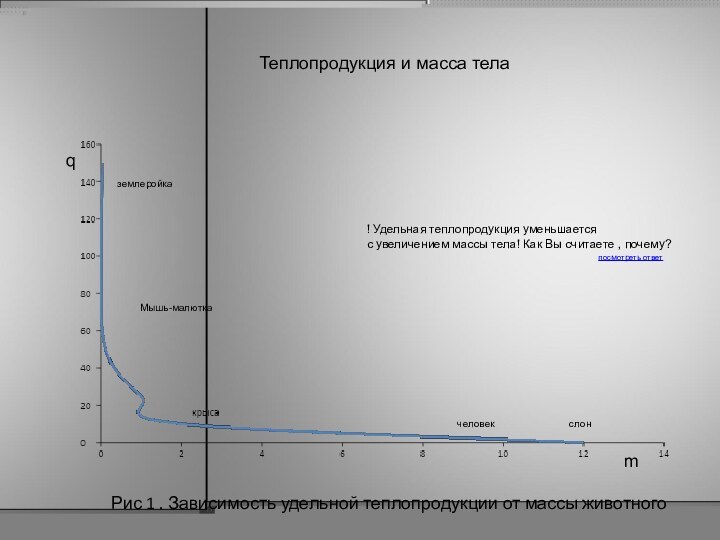
Удельная теплопродукция (g)
g = Q t /µ t
Q t
Количество теплоты выделяющееся в единицу времени
µ t
единица массы животного
Теплопродукция пропорциональна массе животного:
Q t
=к * М
Общая теплопродукция организма :Q орг = Qin + Qext
Слайд 21
а-количество клеток
b- площадь поверхности
Отсюда, удельная теплопродукция (q):
Слайд 22
Рис 1 . Зависимость удельной теплопродукции от массы
животного
q
m
землеройка
слон
человек
! Удельная теплопродукция уменьшается
с увеличением массы тела! Как Вы
считаете , почему?
посмотреть ответ
Теплопродукция и масса тела
Мышь-малютка
Слайд 23
Энтальпия
Живые организмы – открытые термодинамические системы, существуют
в
условиях постоянства давления и температуры.
В этих условиях- для оценки
их жизнедеятельности важен еще
один термодинамический параметр - энтальпия
Энтальпия (Н) - сумма внутренней энергии системы и произведения
объема и давления:
Н = U+P*V
ΔН = Нпрод - Нисход
,
ΔН
(кДж/моль)
!! Отметим, что изменение энтальпии соответствует величине поглощенной
или выделенной теплоты, которую определяют с помощью калориметра
Слайд 24
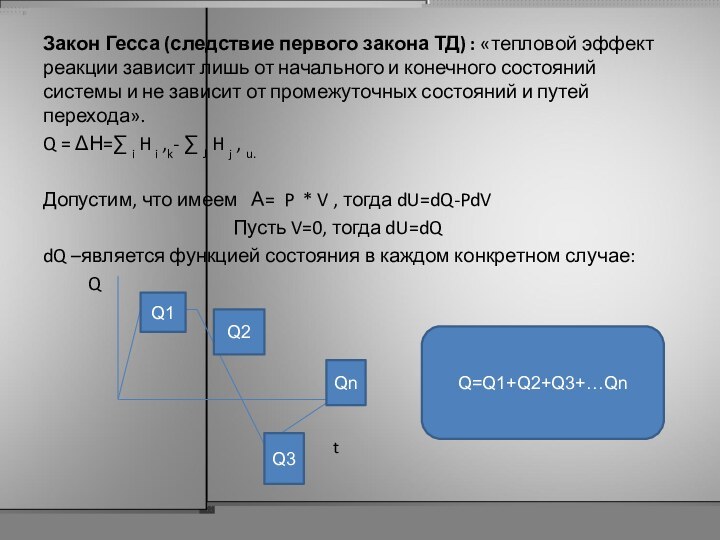
Закон Гесса (следствие первого закона ТД) : «тепловой
эффект реакции зависит лишь от начального и конечного состояний
системы и не зависит от промежуточных состояний и путей перехода».
Q = ΔН=∑ i H i ,k- ∑ J H j , u.
Допустим, что имеем А= P * V , тогда dU=dQ-PdV
Пусть V=0, тогда dU=dQ
dQ –является функцией состояния в каждом конкретном случае:
Q
t
Q1
Q2
Q3
Qn
Q=Q1+Q2+Q3+…Qn
Слайд 25
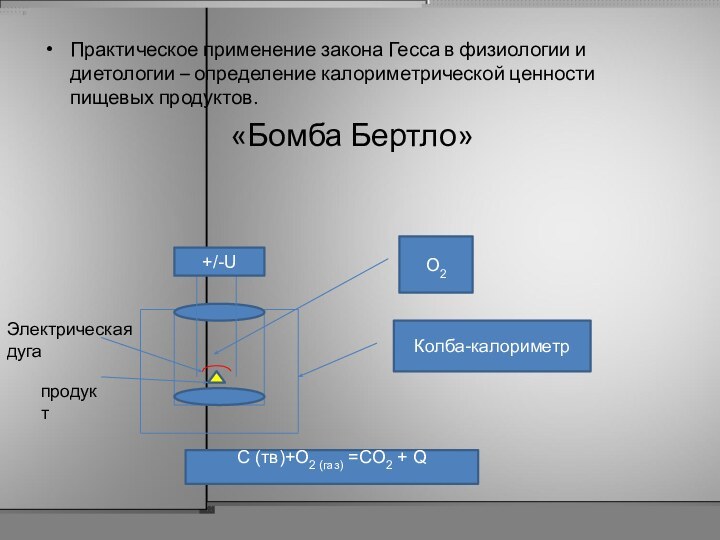
Практическое применение закона Гесса в физиологии и диетологии
– определение калориметрической ценности пищевых продуктов.
«Бомба Бертло»
+/-U
Колба-калориметр
O2
C (тв)+O2 (газ) =CO2 + Q
Электрическая дуга
продукт
термодинамики
(Клаузиуса): «Невозможен процесс, единственным результатом которого являлась бы передача
тепла от более холодного тела к более горячему»
C
x
dC
A
B
grad C= dC / dX
Следствие: Самопроизвольно может совершаться процесс в котором энергия переходит от более высокого уровня к более низкому , т.е. по градиенту
Слайд 27
I – закон не говорит о направлении пути
самопроизвольного процесса.
Возможность протекания Т/Д процессов их направленность
и
предел характеризуют :
Энтропия Свободная энергия
Энтропия (S):
S = Q (3)
T
dS = - dQ / T, отсюда dQ = - TdS
Если dU = dQ+dA (1 й закон Т/Д) , то получим:
dU = dA + TdS
Отношение тепла,
производимого в
обратимом
изотермическом
процессе к
Абсолютной
температуре
Изменение свободной энергии, при совершении работы
dA = dF, тогда получим:
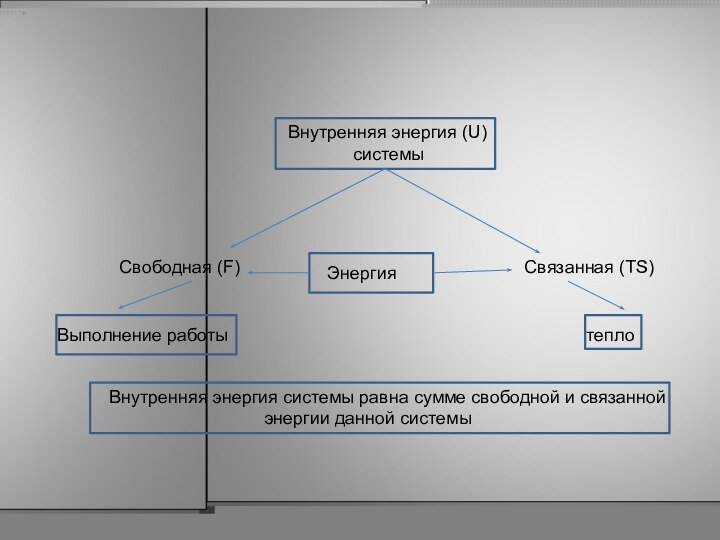
dU = dF + TdS или : U = F + TS
(4)
Слайд 28
Внутренняя энергия системы равна
сумме свободной и связанной
энергии данной системы
Внутренняя энергия
(U)
системы
Свободная (F)
Связанная (TS)
Выполнение работы
Энергия
тепло
Слайд 29
При T = const, связанная энергия определяется энтропией..,
отсюда
чем больше энтропия, тем больше связанной энергии…,
тем
интенсивнее в системе рассевание энергии в виде тепла,
.тем более необратим процесс…
Закономерность
А= dF=dU - TdS
Если процесс обратим, то работа совершенная системой будет равна:
При необратимых процессах, наоборот,
А= dF < dU - TdS
совершенная работа будет меньше изменения свободной энергии
(5)
(6)
Слайд 30
Обобщая вышесказанное с позиций Второго закона Т/Д:
«Любой самопроизвольный
процесс в изолированной системе приводит к уменьшению свободной энергии,
если процесс необратим;
в случае обратимости процесса свободная энергия не изменяется.
Таким образом, свободная энергия системы может увеличится только лишь
за счет поступления энергии из внешней среды
Слайд 31
Математически Второй закон термодинамики может
быть выражен:
d Q
T
0
dS =
Знак больше относится к
необратимым процессам,
а равно к обратимым
Примечание:
(7)
В природе все процессы протекают в направлении уменьшения свободной
энергии и увеличения энтропии.
Если dF (свободная энергия) системы = 0, а dS (энтропия)=max, -
то такая система находится в термодинамическом равновесии.
Слайд 32
Максимально полезная работа, совершаемая системой
А макс – связана
с термодинамическими функциями свободной энергии:
F = U - TS,
и полного термодинамического потенциала:
G = U+ pv- TS,
которые определяются функциями F =F (T, v), а G = (T, p), соответственно.
dA макс=< -d(U-TS)=TdS-dU=-(dF)T,V
При Т, v=const.:
При Т, p=const.:
dAмакс =< -d(U+pv-TS)=TdS-dU-pdv=-(dG)T,p
dG<0 указывает на необратимость процессов
Слайд 33
Применительно к биохимическим реакциям, изменения объема
и давления
незначительны:
dF=-SdT-pdv
dG=-SdT+vdp=dF+pdv+vdp
Δ F
≈
ΔG
Таким образом, на практике можно вычислять изменения
свободной энергии (F) и полного термодинамического потенциала (G)
Применительно, к конкретной реакции:
ΔG0
=
-RT ln K+ RT ln (c’1 v1)* (c’2 v2 )
(c1 v1)* (c2 v2 )
где с – концентрация веществ в смеси
v- стехиометрические коэффициенты
Слайд 34
При этом dA = 0.
В этом случае
система деградирована и не способна совершать
работу.
Для выхода системы
из подобного состояния необходим приток
энергии из вне.
Таким образом, в системах могут происходить лишь процессы ,
связанные с рассеиванием энергии, а так же с уменьшением
свободной энергии, в конечном счете приводя к установлению Т/Д
равновесия.
Отсюда проблема применимости 2-го закона Т/Д к био- системам.
Жизнь – невероятное состояние ?!
Слайд 35
Таким образом, эволюционный критерий направленности необратимых
изменений в изолированных системах, заключается в том что они
всегда идут с увеличением энтропии (dS>0) до ее максимальных значений при окончании процесса и установлении термодинамического равновесия.
Увеличение энтропии означает падение степени упорядоченности и организованности в системе, ее хаотизацию.
Слайд 36
ОБЩАЯ ХАРАКТЕРИСТИКА ОТКРЫТЫХ СИСТЕМ.
Открытые системы -
это термодинамические системы, которые обмениваются с окружающими телами (
средой ) , веществом , энергией и импульсом .
Если отклонение открытой системы от состояния равновесия невелико , то неравновесное состояние можно описать теми же параметрами (температура , химический потенциал и другие) , что и равновесное . Однако отклонение параметров от равновесных значений вызывают потоки вещества и энергии в системе . Такие процессы переноса приводят к производству энтропии .
Примерами открытых систем являются : биологические системы , включая клетку , системы обработки информации в кибернетике , системы энергоснабжения и другие .
Слайд 37
Для поддержания жизни в системах от клетки до
человека необходим постоянный обмен энергией и веществом с окружающей
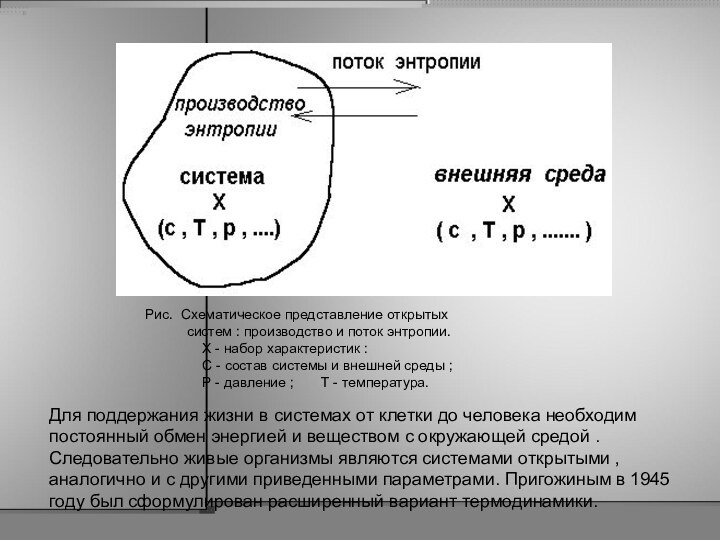
средой . Следовательно живые организмы являются системами открытыми , аналогично и с другими приведенными параметрами. Пригожиным в 1945 году был сформулирован расширенный вариант термодинамики.
Рис. Схематическое представление открытых
систем : производство и поток энтропии.
Х - набор характеристик :
С - состав системы и внешней среды ;
Р - давление ; Т - температура.
Слайд 38
Рассмотрим свойства организма как -термодинамически
- открытой системы, в которой протекают химические реакции. Биохимические
реакции на всех стадиях являются каталитическими, катализаторами служат белки-ферменты. Изменение энтропии такой системы выражается суммой энтропии, производимой внутри системы dSi и энтропии поступающей извне dSе:
dS = dSi+ dSе (8)
При этом dSi>0, т.к. если организм изолировать, то dSе=0, и энтропии будет только возрастать; dSi – производство энтропии в результате внутренних реакций.
Отсюда возможны следующие варианты энтропии:
1) dS =0, dSe =- dSi<0 - из данного уравнения следует возможность стационарного, но не равновесного состояния, когда
производимая энтропия уходит во внешнюю среду;
2) -dSe > dSi. То dS <0 и наконец, 3) -dSe < dSi. то dS >0
Термодинамика открытых систем
Слайд 39
Энтропия в организме может оставаться постоянной величиной или
увеличиваться или уменьшаться, если поток отрицательной энтропии из среды
в организм больше потока энтропии, образующейся в организме.
dS = dSi+ dSе;
dt
dt
dt
Скорость изменения энтропии в организме равна алгебраической
сумме скорости производства энтропии внутри организма и скорости
поступления энтропии из среды в организм
Восполнение свободной энергии из среды происходит за счет поступления
питательных веществ в организм, а выведение энтропии за счет удаления
продуктов обмена и теплоты
Математическое выражения
2 го Закона для биосистем.
(9)
Слайд 40
Потенциально, возможно состояние когда скорость производства
энтропии внутри
системы равна скорости поступления энтропии из среды:
dSi= -dSе;
dt
dt
Т.е. возникает состояние когда параметры систем не измены во времени,
при этом происходит обмен веществом и энергией с окружающей средой,
- такое состояние системы называют «Стационарным».
(10)
Слайд 41
ДИССИПАТИВНЫЕ СИСТЕМЫ
Каждая система состоит из элементов (подсистем)
. Эти элементы находятся в определенном порядке и связаны
определенными отношениями. Структуру системы можно назвать организацию элементов и характер связи между ними.
В реальных физических системах имеются пространственные и временные структуры .
Формирование структуры - это возникновение новых свойств и отношений в множестве элементов системы .
В процессах формирования структур играют важную роль понятия и принципы :
Постоянный отрицательный поток энтропии .
Состояние системы в дали от равновесия .
Нелинейность уравнений описывающих процессы .
Коллективное (кооперативное) поведение подсистем .
Универсальный критерий эволюции Пригожина - Гленсдорфа.
Слайд 42
Формирование структур при необратимых процессах должно сопровождаться
качественным скачком (фазовым переходом) при достижении в системе критических
значений параметров. В открытых системах внешний вклад в энтропию (2.1) d S в принципе можно выбрать произвольно , изменяя соответствующим образом параметры системы и свойства окружающей среды . В частности энтропия может уменьшаться за счет отдачи энтропии во внешнюю среду , т.е. когда d S < 0 . Это может происходить , если изъятие из системы в единицу времени превышает производство энтропии внутри системы , то есть
Слайд 43
Чтобы начать формирование структуры , отдача энтропии
должна превысить некоторое критическое значение . В сильно неравновесном
расстоянии переменные системы удовлетворяют нелинейным уравнениям .
Таким образом , можно выделить два основных класса необратимых процессов :
1. Уничтожение структуры вблизи положения равновесия . Это универсальное свойство систем при произвольных условиях .
2. Рождение структуры вдали от равновесия в открытой системе при особых критических внешних условиях и при нелинейной внутренней динамики
Слайд 44
Пространственные , временные или пространственно-временные структуры , которые
могут возникать вдали от равновесия в нелинейной области при
критических значениях параметров системы называются диссипативными структурами (системами).
В этих структурах взаимосвязаны три аспекта :
1. Функция состояния , выражаемая уравнениями .
2. Пространственно - временная структура , возникающая из-за неустойчивости .
3. Флуктуации , ответственные за неустойчивости .
Слайд 45
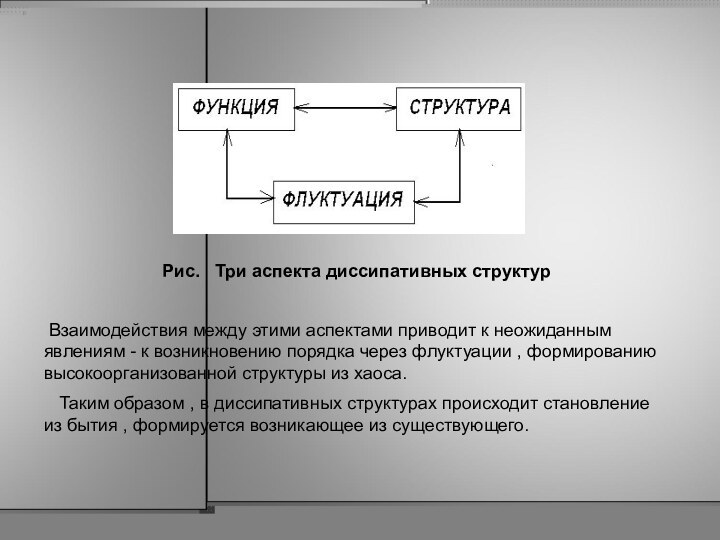
Рис. Три аспекта диссипативных структур
Взаимодействия
между этими аспектами приводит к неожиданным явлениям - к
возникновению порядка через флуктуации , формированию высокоорганизованной структуры из хаоса.
Таким образом , в диссипативных структурах происходит становление из бытия , формируется возникающее из существующего.
Слайд 46
Соотношения Онзагера
В организме имеет место сопряжение многих химических

и физико-химических
процессов.
При этом соотношение между значениями движущих
сил и скоростей процессов
является определяющим в термодинамике биологических систем.
Например, представляет интерес исследование взаимосвязи процессов
переноса через мембрану теплоты, вещества и заряженных частиц и т.п.
Пусть х –движущая сила, а J – значение потока, в таком случае энтропия:
d Si
dT
=
(1/T) XJ>0
Пусть система открытая и находится вблизи Т/Д равновесия, тогда процессы
Х и J будут связанны соотношением: J=LX (где L-линейный коэффициент силы)
=const.). Введем обозначения - L11 и L22 –зависимость потока от «своей» силы и
L12 и L21 влияние потоков друг на друга
Если в такой системе существуют и протекают несколько процессов,
каждый из которых характеризуется скоростью и движущей силой, то
возможно взаимодействие этих процессов. При этом движущая сила
одного процесса, будет определяться движущей силой других процессов:
(11)
(коэф. Онзагера).
Слайд 47
Пусть имеем два взаимодействующих процесса (J1 X 1
) и (J2 X 2 ).
Тогда потоки будут определяться,
как:
J 1 = L11X 1+L12X2
J 2 = L21X 1+L22X2
Где L11 и L21 - коэффициенты взаимности процессов
L 12 = L 21
Если поток 1-го необратимого процесса испытывает влияние
сродства Х2 необратимого второго процесса, через посредство
коэффициентов L 12 , то и поток 2-го будет испытывать влияния
cродства X1 через посредство тех же коэффициентов.
- соотношение Онзагера
(12)
(13)
Вблизи равновесия
выполняется соотношение:
Тогда если процесс I1, X1 идет против градиента силы X1 (I1, X1 <0) за счет Е
второго процесса ((I2, X2> 0), то мерой сопряженности процессов (q) будет:
L12
__________
L11 L 22
q =
(14)
Если q = 0 нет сопряжения
q=1 сопряжение
полное
Слайд 48
Пусть имеем два взаимодействующих процесса (J1 X 1
) и (J2X2 ).
Тогда, J1 = L11X1+L12X2
J2 = L21X1+L22X2
L11 и L21 - коэффициенты взаимности процессов
Термодинамические критерии устойчивости стационарных
процессов. Теорема Пригожина
Условие:
Открытая система, с протекающими необратимыми процессами, где справедливы линейные соотношения:
В= J1X 1+J2X2 >0
dS = dSi+ dSе
Пусть система находится в стационарном состоянии, где выполняется
соотношения Онзагера:
dt
dt
dt
= 0 ;
dSi
dt
>0 и
dSе
dt
>0
при
где I1 X1 –находится в стационарном состоянии, то I 1 = 0;
В =
Т
diS
dt
=
J1X1+J2X2
=
L11X12 +
2 L11X1X2 + L22X2 2
При приближении к стационарному состоянию I1 X1
изменяется так, что I =0; отсюда:
dB
dX1
=
X2=const
2
L11X1 + L12X2 = 2 I1
Так как I1 =I1
= 0 то
dB
dX1
X2=const
= 0
Слайд 49
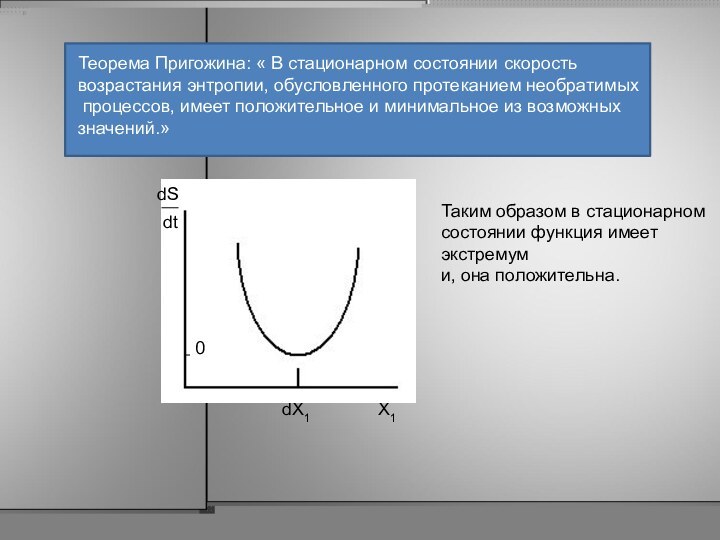
Теорема Пригожина: « В стационарном состоянии скорость
возрастания
энтропии, обусловленного протеканием необратимых
процессов, имеет положительное и минимальное
из возможных
значений.»
X1
dX1
dt
dS
Таким образом в стационарном
состоянии функция имеет
экстремум
и, она положительна.
0
Слайд 50
Итак, состояние всякой линейной открытой системы с независящими
от времени краевыми условиями всегда изменяется в направлении уменьшения
производства энтропии P = d S / d t пока не будет достигнуто состояние текущего равновесия , при котором производство энтропии минимально :
d P < 0 (условие эволюции)
P = min , d P = 0 (условие текущего равновесия)
d P/ d t < 0
Слайд 51
В живых системах, как считается,
можно приравнять диссипативную функцию к интенсивности теплопродукции, а следовательно,
интенсивности дыхания и гликолиза, которые в основном и определяют теплопродукцию организма. При этом теорема Пригожина приобретает простой биологический смысл, так как сводится к утверждению, что в процессе возрастных изменений организмов происходит непрерывное снижение интенсивности этих процессов.
Многочисленные экспериментальные данные, полученные в последнее время, достаточно хорошо подтверждают это положение.
Слайд 52
Против теоремы Пригожина–Виам выдвинуто два основных возражения:
1)
считается, что эта теория все же недостаточно проверены экспериментально;
2) ограничения, накладываемые на системы термодинамикой линейных необратимых процессов, не выполняются во время развития и роста животных.
У человека после рождения основной обмен и скорость теплопродукции, рассчитанная на единицу веса, заметно возрастает и лишь затем начинает постепенно снижаться. С точки зрения термодинамики необратимых процессов это означает, что после рождения происходит изменение внешних параметров системы, которое должно сопровождаться переходом системы в новое стационарное состояние (теорема Пригожина выполняется только при неизмененных внешних параметрах). Характерно, что для внутриутробного развития млекопитающих получены совершенно иные данные, чем для только что родившихся животных: на протяжении изученных стадий внутриутробного развития коров происходит непрерывное снижение основного обмена зародышей.
Слайд 53
Согласно термодинамической теории Пригожина – Виам, можно считать,

что процесс развития, роста и старения организмов представляет собой
процесс непрерывного уменьшения функции внешней диссипации.
Каждый новый организм начинает свое развитие с высокого уровня удельной скорости продукции энтропии. Следовательно, в жизни организмов должен существовать период, когда происходит процесс конститутивного уклонения от стационарного состояния, сопровождающийся не уменьшением, а увеличением функции внешней диссипации.
С точки зрения термодинамики необратимых процессов представляется невероятным, чтобы отдельно существующая система, какой является зародыш, растущий организм или взрослое животное, могла бы сама собой при неизменных внешних параметрах устойчиво уклоняться от стационарного состояния.
Этот процесс, однако, вполне мыслим в период возникновения половых клеток и, в частности, в оогенезе. С точки зрения термодинамической теории развития организмов в оогенезе происходит процесс омоложения системы, а на всех остальных этапах жизни организма – процесс старения. Отличия периодов развития, роста и старения, с этой точки зрения, заключаются в скорости процесса старения.
Процесс зародышевого развития является одним из самых трудных для объяснения с точки зрения термодинамической теории Пригожина – Виам, так как многочисленные иследования дыхания зародышей показали, что в расчете на яйцо происходит значительное увеличение интенсивности дыхания и теплопродукции в этот период. Даже Пригожин вынужден был признать, что на ранних стадиях развития его теория не согласуется с имеющимися экспериментальными данными.
Слайд 54
Дополнительная литература
1. Базаров И.П. Термодинамика. - М.: Высшая

школа, 1991 г.
2. Гленсдорф П. , Пригожин И. Термодинамическая
теория структуры , устойчивости и флуктуаций. - М.: Мир, 1973 г.
3. Карери Д. Порядок и беспорядок в структуре материи. - М.: Мир, 1995 г.
4. Курдюшов С.П. , Малинецкий Г.Г. Синергетика - теория самоорганизации. Идеи , методы перспективы. - М.: Знание, 1983 г.
5. Николис Г. , Пригожин И. Самоорганизация в неравновесных системах. - М.: Мир, 1979 г.
6. Николис Г. , Пригожин И. Познание сложного. - М.: Мир, 1990 г.
7. Перовский И.Г. Лекции по теории дифференциальных уравнений. - М.: МГУ, 1980 г.
8. Попов Д.Е. Междисциплинарные связи и синергетика. - КГПУ, 1996 г.
9. Пригожин И. Введение в термодинамику необратимых процессов. - М.: Иностранная литература , 1960 г.
10. Пригожин И. От существующего к возникающему. - М.: Наука, 1985 г.
11. Синергетика , сборник статей. - М.: Мир, 1984 г.
12. Хакен Г. Синергетика . - М.: Мир , 1980 г.
13. Хакен Г. Синергетика . Иерархия неустойчивостей в самоорганизующихся системах и устройствах . - М.: Мир , 1985 г.
14. Шелепин Л.А. В дали от равновесия. - М.: Знание, 1987 г.
15. Эйген М. , Шустер П. Гиперцикл . Принципы самоорганизации макромолекул . - М.: Мир , 1982 г.
16. Эткинс П. Порядок и беспорядок в природе. - М.: Мир , 1987 г