- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрические построения, необходимые при выполнении чертежей
Содержание
- 2. Цель: сформировать у студентов навыки выполнения чертежей предметов с использованием геометрических построений.
- 3. О б ъ я с н е
- 4. Деление окружности на четыре равные части.
- 5. Деление окружности на 8 равных частей.
- 6. Деление окружности на 3 и 6 частей.
- 7. Для деления окружности на 6
- 8. Деление окружности на 12 частей.
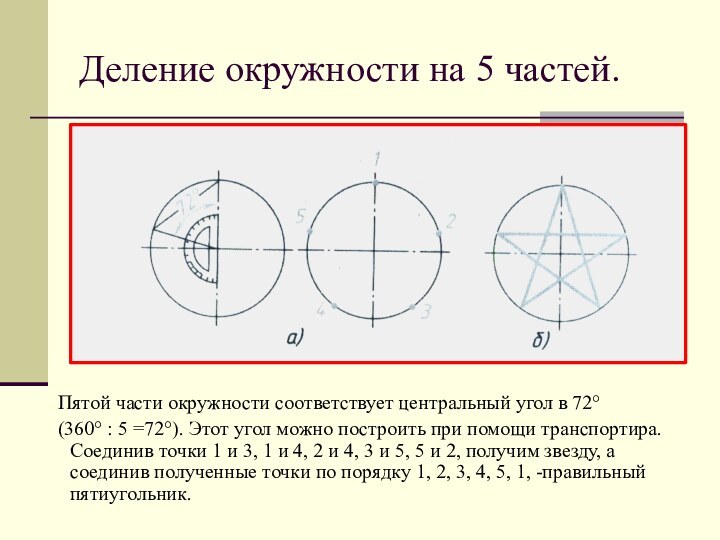
- 9. Деление окружности на 5 частей. Пятой
- 10. Чтобы разделить окружность с
- 11. С о о б щ е н
- 12. Закрепление. Скажите, на сколько частей нужно разделить окружность, чтобы выполнить чертеж торгового знака?
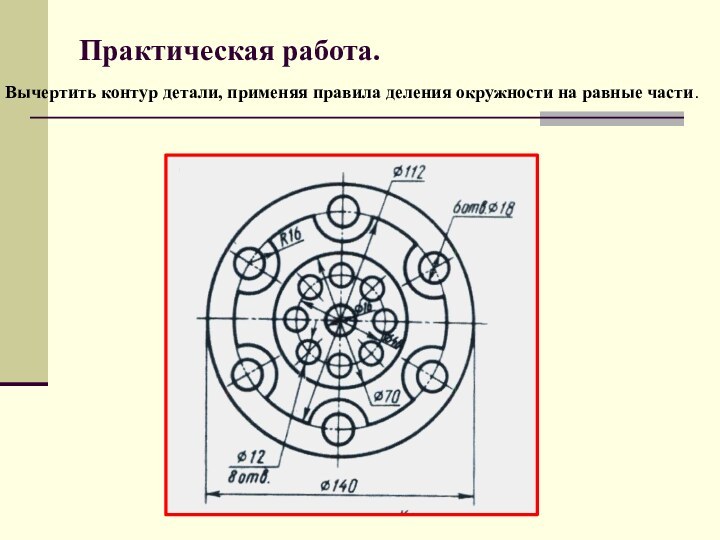
- 13. Практическая работа. Вычертить контур детали, применяя правила деления окружности на равные части.
- 14. Итоги урока. Что нового вы узнали на
- 15. Скачать презентацию
- 16. Похожие презентации
Цель: сформировать у студентов навыки выполнения чертежей предметов с использованием геометрических построений.








Слайд 2
Цель:
сформировать у студентов навыки выполнения чертежей
предметов с использованием геометрических построений.
Слайд 4
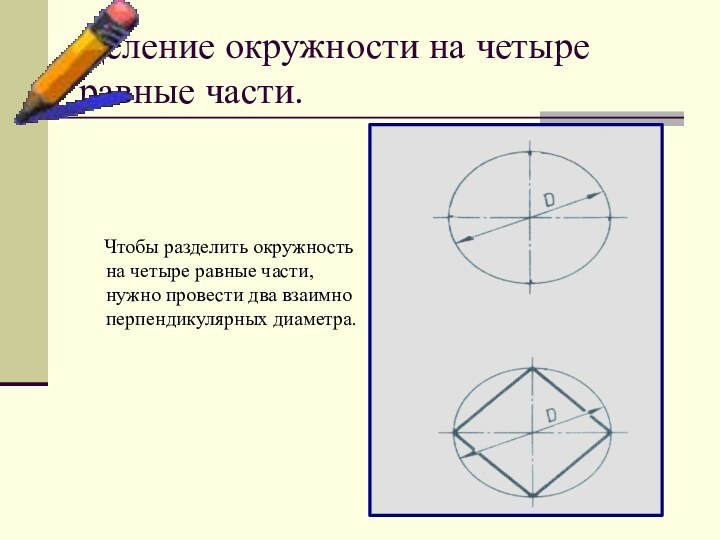
Деление окружности на четыре равные части.
Чтобы разделить окружность на четыре равные части, нужно
провести два взаимно перпендикулярных диаметра.
Слайд 5
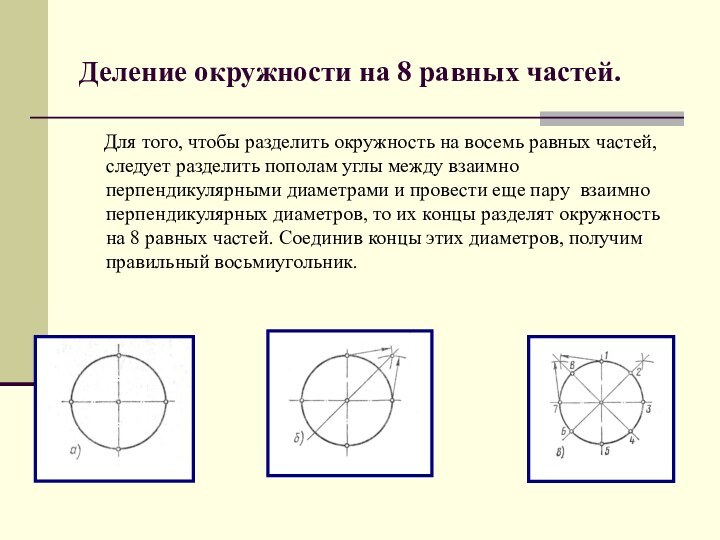
Деление окружности на 8 равных частей.
Для того, чтобы разделить окружность на восемь равных
частей, следует разделить пополам углы между взаимно перпендикулярными диаметрами и провести еще пару взаимно перпендикулярных диаметров, то их концы разделят окружность на 8 равных частей. Соединив концы этих диаметров, получим правильный восьмиугольник.
Слайд 6
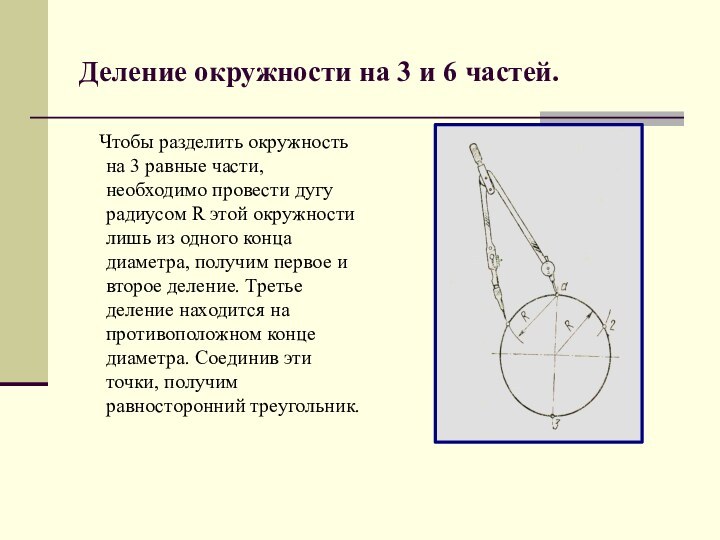
Деление окружности на 3 и 6 частей.
Чтобы разделить окружность на 3 равные части, необходимо
провести дугу радиусом R этой окружности лишь из одного конца диаметра, получим первое и второе деление. Третье деление находится на противоположном конце диаметра. Соединив эти точки, получим равносторонний треугольник.Слайд 7 Для деления окружности на 6 частей
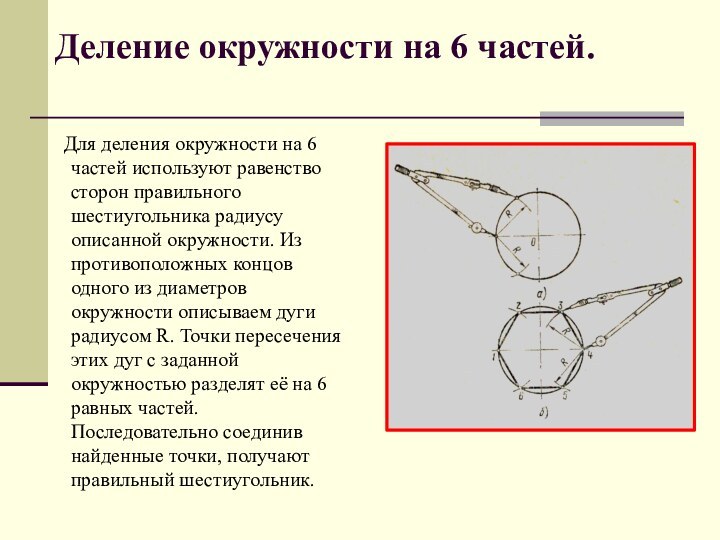
используют равенство сторон правильного шестиугольника радиусу описанной окружности. Из
противоположных концов одного из диаметров окружности описываем дуги радиусом R. Точки пересечения этих дуг с заданной окружностью разделят её на 6 равных частей. Последовательно соединив найденные точки, получают правильный шестиугольник.Деление окружности на 6 частей.
Слайд 8
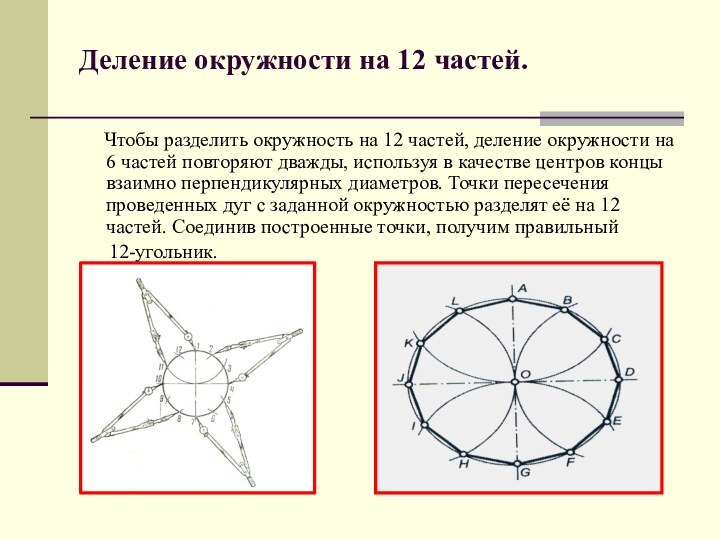
Деление окружности на 12 частей.
Чтобы разделить окружность на 12 частей, деление окружности на
6 частей повторяют дважды, используя в качестве центров концы взаимно перпендикулярных диаметров. Точки пересечения проведенных дуг с заданной окружностью разделят её на 12 частей. Соединив построенные точки, получим правильный12-угольник.