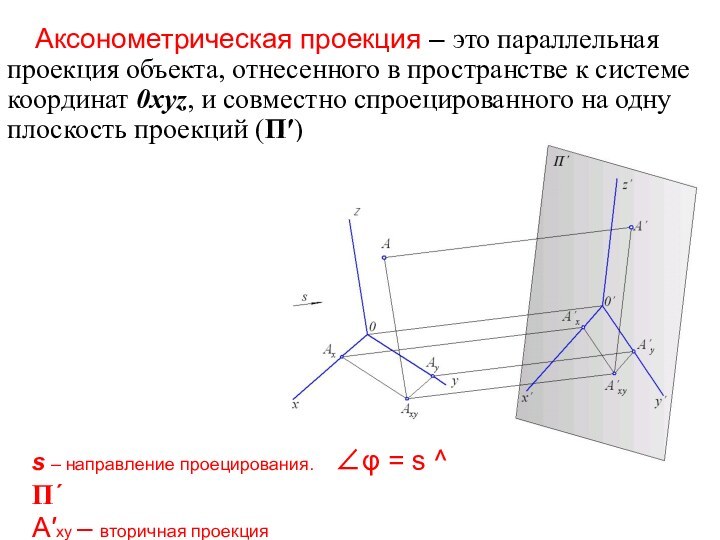
в пространстве к системе координат 0xyz, и совместно спроецированного
на одну плоскость проекций (П′)s – направление проецирования. ∠φ = s ^ П´
А′xy – вторичная проекция
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





















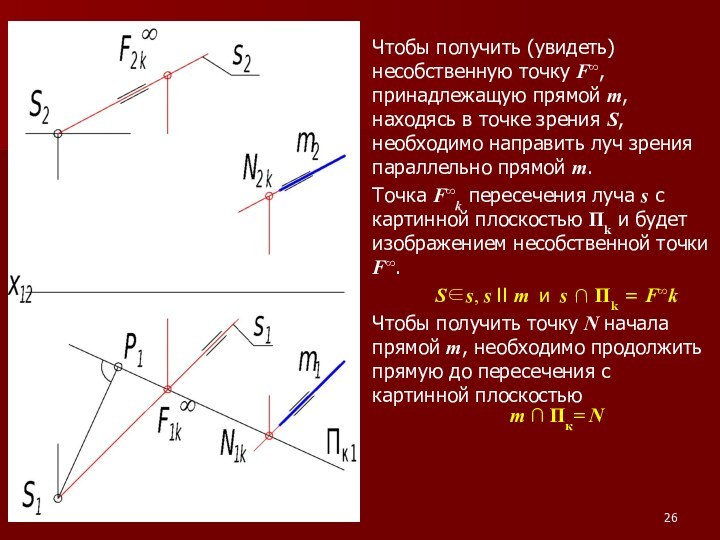




s – направление проецирования. ∠φ = s ^ П´
А′xy – вторичная проекция
Расположение пространственной системы координат 0xyz относительно плоскости проекций