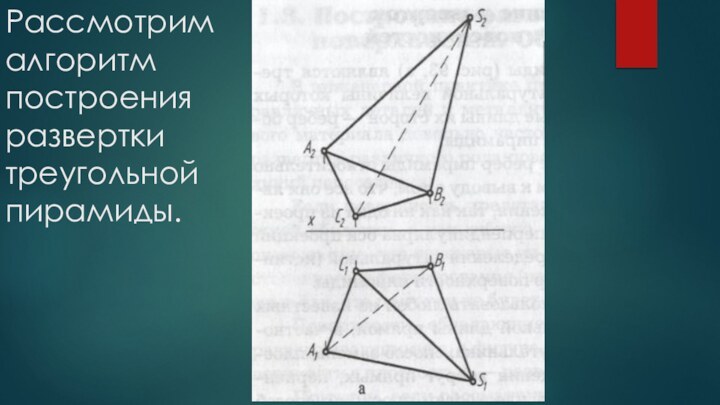
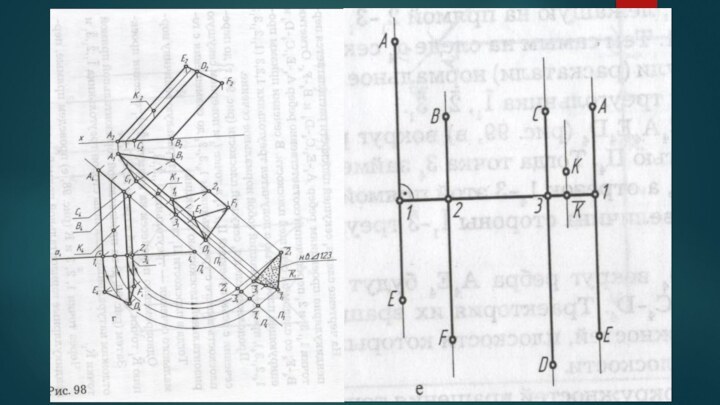
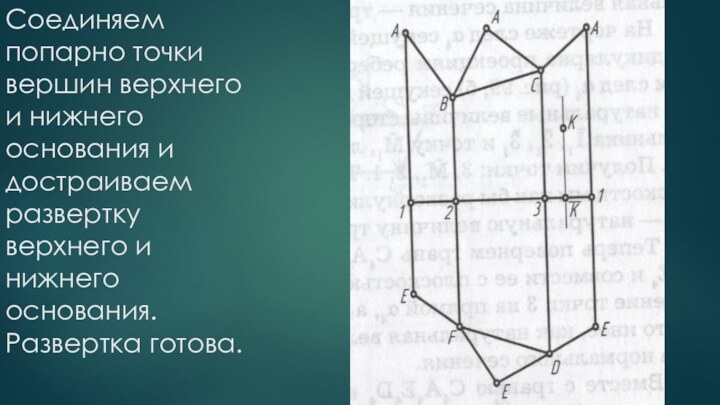
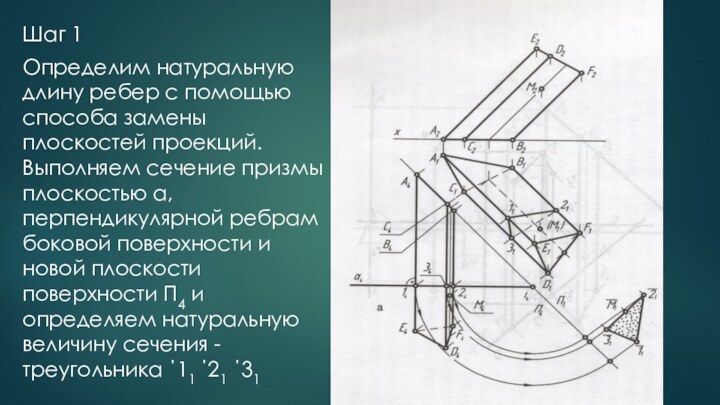
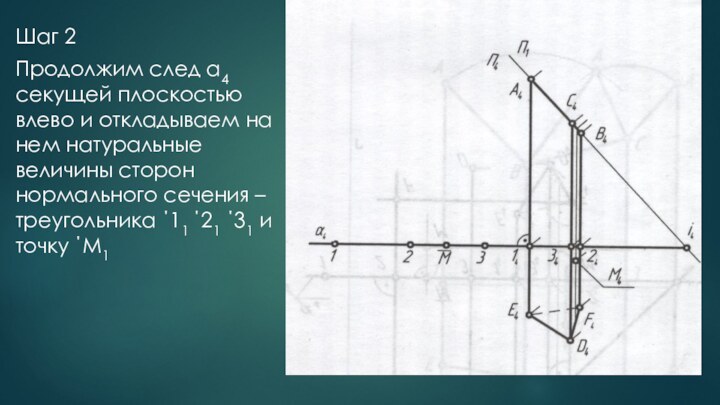
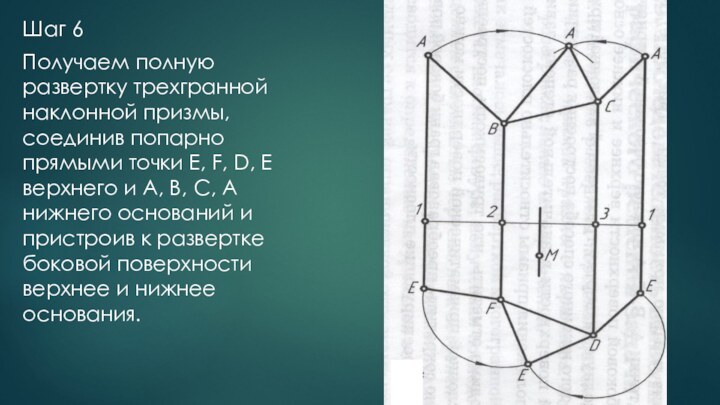
деформирования(разгибания) совместить с плоскостью так, что при этом не
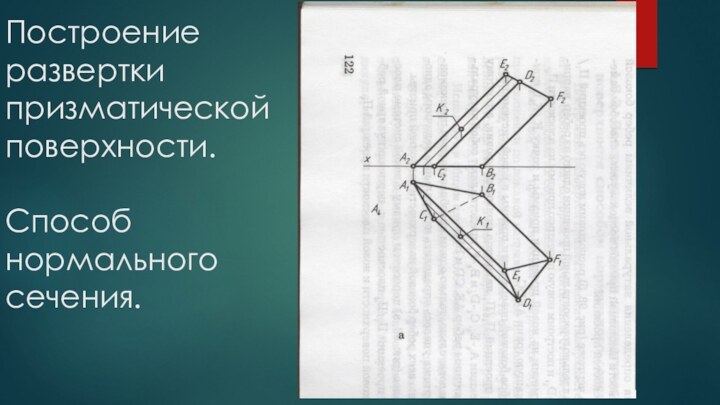
будет ни складок, ни разрывов ,называются развертывающимися, а фигура, полученная от совмещения поверхности с плоскостью – разверткой.К числу развертывающихся поверхностей относятся все многогранные поверхности.