- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методическая разработка раздела программы по математике Преобразование задач в начальной школе. УМК ШКОЛА РОССИИ
Содержание
- 2. Важнейшая составляющая начального общего образования.Усвоенные в начальном
- 3. Особенности учебной программы
- 4. РЕЗУЛЬТАТЫ АНКЕТИРОВАНИЯ
- 5. Анализ УМК
- 6. ЦЕЛЬ Повышение уровня умения решать задачи
- 7. Возрастные особенности младших школьников Уровень наглядно
- 8. Система упражнений1) расчленение задачи на элементарные условия
- 9. Выпускник научится: анализировать задачу, устанавливать зависимость между
- 12. ТИПЫ ЗАДАНИЙ1 тип задания - узнавание«В лагерь
- 13. ВИДЫ УПРАЖНЕНИЙИзменение поставленного к условию задачи вопроса.Изменение
- 14. Этапы и приёмы работы1.Этап восприятия и осмысления
- 15. 4.Этап осуществления плана решения5.Этап проверки1.По действиям с
- 17. Подготовительная работа1.Разбор задачиЦель: повторить общие приемы работы
- 18. Когда на военной базе противника отремонтировали 8
- 19. 2. Постановка вопроса к условию задачиЦель: обобщить
- 20. 3.Составление условия задачи по данному вопросу.Цель: обобщить
- 21. Обучение преобразованию задач
- 22. 1 этап«Катя, Лена и Наташа купили по
- 23. 2 этап
- 24. ПАМЯТКАПрочитай задачуСоставь план решенияРеши задачуСделай краткую записьСформулируй
- 25. 3 этап дифференцированный подход Задача Работа
- 26. Деятельность учащихсяВыделяют задачи из предложенных текстовМоделируют с
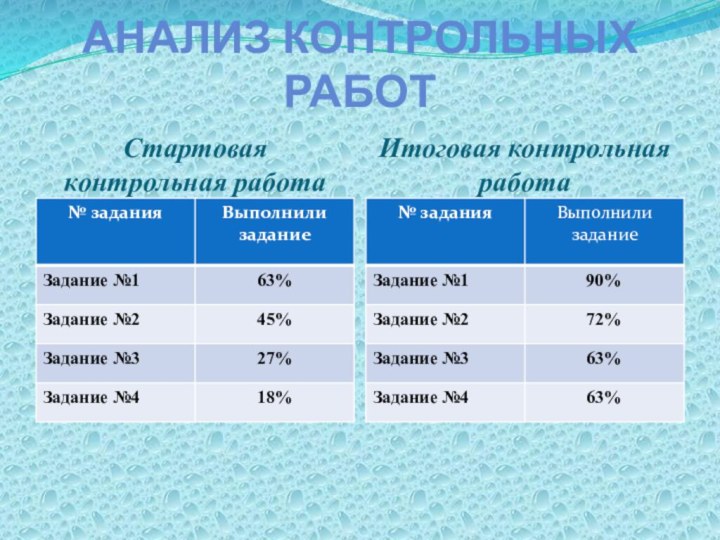
- 27. Анализ контрольных работСтартовая контрольная работаИтоговая контрольная работа
- 28. Тематическое планирование1 класс2 класс
- 30. 3 класс4 класс
- 32. Скачать презентацию
- 33. Похожие презентации



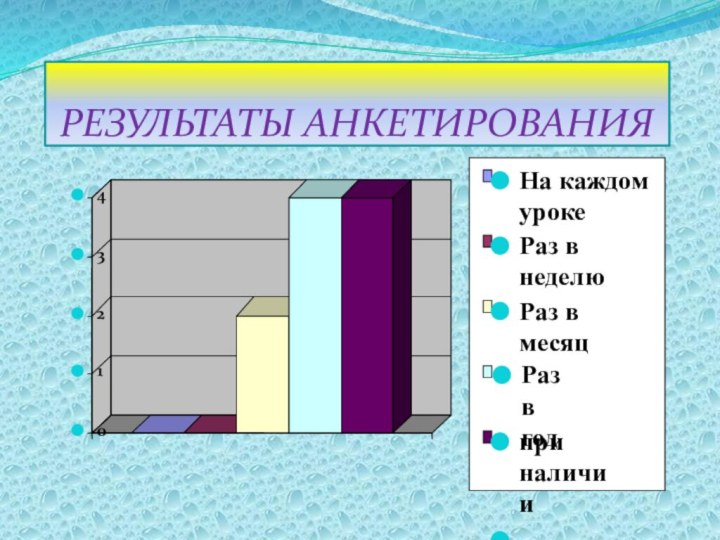

























Слайд 3
Особенности учебной программы
Система
подбора задач, определение времени и последовательности введения задач того
или иного вида обеспечивают благоприятные условия для сопоставления, сравнения, противопоставления задач, сходных в том или ином соотношении, а также для рассмотрения взаимообратных задач. При таком подходе дети с самого начала приучаются проводить анализ задачи,устанавливая связь между данными и искомым,
и осознанно выбирать правильное действие для
ее решения. Решение некоторых задач основано
на моделировании описанных в них
взаимосвязей между данными и искомым.
Слайд 6 ЦЕЛЬ Повышение уровня умения решать задачи с помощью обучения
преобразованию задач
Задачи
Познавательные
Развивающие Воспитательные
1.Способствовать осознанию смысла арифметических действий и математических отношений
2.Формирование умения вести поиск информации и работать с ней
4.Понимание практического значения математических знаний
1.Развитие
-воображения
-логического мышления
-речи
2.Пробуждение интереса к математике
3.Повышение мотивации к изучению математики
1.Укрепление связи обучения с жизнью
2.Способствовать духовно-нравственному развитию и воспитанию.
Слайд 7 Возрастные особенности младших школьников Уровень наглядно – образного
мышления (дооперациональный уровень интеллектуального развития ) Основан на логике эмпирических связей вещей,
усвоенных при их практическом использовании. Создание Формирование наглядно – схематического мышления. условий Формирование логического мышления Сопровождается процессом освоения моделирования как формы продуктивного мышления Основа – развитие
анализа и синтеза
Слайд 8
Система упражнений
1) расчленение задачи на элементарные условия и
требования
2) выявление связей и зависимостей между отдельными данными между
данными и требованием3) построение схематической модели к задаче
4) перекодировка задачи на другой язык
ТРУДНОСТИ
связанные с возрастными особенностями мышления детей
проблема понимания работа со вспомогательной
текста графической моделью
Слайд 9
Выпускник научится:
анализировать задачу, устанавливать зависимость между величинами
и взаимосвязь между условием и вопросом задачи, определять количество
и порядок действий для решения задачи, выбирать и объяснять выбор действий;решать учебные задачи и задачи связанные с повседневной жизнью арифметическим способом;
оценивать правильность хода решения и реальность ответа на вопрос задачи.
Выпускник получит возможность научиться:
находить разные способы решения задачи
Ожидаемые результаты
Слайд 11
Уровни умения решать задачи
I уровень – репродуктивное
узнавание (ученический) - позволяет учащемуся при повторном восприятии информации
отличать правильное ее использование от неправильного.II уровень– репродуктивное алгоритмическое действие (типовой) способность самостоятельно воспроизводить информацию, применять ее в разнообразных типовых случаях.
III уровень – продуктивное эвристическое действие (эвристический) способность самостоятельно воспроизводить и преобразовывать усвоенную информацию .
IV уровень – продуктивное творческое действие (творческий) способность использовать информацию для получения объективно новой информации в процессе нахождения и обсуждения новых свойств известных объектов; нахождения и исследования новых методов деятельности с объектами; нахождения новых объектов, свойств и качеств.
Слайд 12
ТИПЫ ЗАДАНИЙ
1 тип задания - узнавание
«В лагерь приехали
2 группы детей по 9 человек в каждой. Сколько
мальчиков приехало в лагерь, если девочек было 11 человек?»2 тип задания – типовое
«На экскурсию в музей пришли ребята. Их разделили на 4 группы по 5 человек в каждой. Сколько учеников пришло из школы, если из детского сада пришло 12 ребят?»
3 тип задания – реконструкция
«В магазин привезли ∆ ящиков огурцов по ◊ кг в каждом. Сколько огурцов продали, если осталось ░ кг?»
4 тип задания - дополнение
"Билеты на самолет до Архангельска купили 45 человек. Первым рейсом улетело 15 человек, вторым столько же,..."
Задание: необходимо поставить вопрос к данной задаче и решить ее.
Слайд 13
ВИДЫ УПРАЖНЕНИЙ
Изменение поставленного к условию задачи вопроса.
Изменение условия
задачи без изменения поставленного вопроса.
Изменение условия и вопроса задачи.
Преобразование
данных задач в задачи родственных им видов, т.е в «задачи, в которых величины связаны одинаковой зависимостью.Составление аналогичных задач, т.е. составление задач, имеющих одинаковую математическую структуру, не изменяя связь между данными и искомым.
Составление обратных задач.
Слайд 14
Этапы и приёмы работы
1.Этап восприятия и осмысления текста
задачи
2.Этап поиска плана решения
3.Этап составления плана решения
ПРИЁМЫ
1.Получение информации о
содержании задачи.2.Представление ситуации.
3.Переформулирование текста задачи
4.Определение вида задачи. Выделение величин данных в задаче.
5.Деление задачи на смысловые части по утверждениям.
6.Уточнение: является ли текст задачей?
7.Беседа на понимание текста задачи. Осмысление характеристик задачи.
8.Построение вспомогательной модели
1.От требования к данным.
2. От условия к требованию.
1.Построение плана решения по вспомогательной модели.
2. Построения «Дерева рассуждений».
3.Составление программы действий.
4.Запись шагов решения в виде выражения.
Слайд 15
4.Этап осуществления плана решения
5.Этап проверки
1.По действиям с кратким
пояснением к каждому выполненному действию.
2.По действиям с полным пояснением
к каждому выполненному действию.3.По действиям с записью вопросов.
4. В виде выражения, преобразуемого после вычислений в равенство, без записи шагов по составлению выражения.
1.Решение задачи другим способом.
2.Прогнозирование результата.
3.Сравнение с готовым верным решением
4.Повторное решение тем же способом методом с обоснованием каждого шага решения.
5.Составление и решение обратной задачи.
Слайд 17
Подготовительная работа
1.Разбор задачи
Цель: повторить общие приемы работы над
задачей, актуализировать знания детей о структурных компонентах задачи
Например,
«В
музей на экскурсию пришли 2 группы ребят по 9 человек в каждой. Сколько было ребят из первого класса, если из группы продленного дня было 8 человек?»- О чем говорится в задаче?
- Что нам известно?
- Какой вопрос ставится в задаче? Можем ли мы сразу на него ответить?
- Что нам для этого нужно найти?
- Из скольких простых задач состоит данная задача?
- С помощью какого действия мы решим первую простую задачу?
- С помощью какого действия мы решим вторую простую задачу?
Далее проходит работа по выделению в задаче условия, требования и связей между ними: - назовите условие задачи; - назовите требование, которое ставится в задаче; - какие слова указывают на выбор арифметического действия?
Затем составляется краткая запись
После этого дети оформляют в тетради решение задачи.
Слайд 18
Когда на военной базе противника отремонтировали 8 тяжелых
и 5 легких танков, то осталось отремонтировать еще 9
танков. Сколько на базе было танков?-Можем ли мы данный текст назвать задачей?
- Почему?
- Давайте на магнитной доске соберем краткую запись.
- Можно ли сразу ответить на вопрос
задачи?
- Что нужно узнать сначала?
-Что потом?
Дети отвечают.
-Запишем задачу с планом и решением.
Один ученик работает у доски.
- Мы точно выполнили задание штаба и теперь можем отдохнуть.
Было 9т отремонтировали
8т и 5т осталось ?т
Слайд 19
2. Постановка вопроса к условию задачи
Цель: обобщить знания
о связях между данными и искомым.
Детям предлагается
разбиться на группы. Каждая группа выполняет следующее задание: подобрать к условию соответствующий вопрос. Учащиеся устанавливают, что можно узнать по определенным данным.Например, даны условия задач:
1. В саду росло 3 яблони, 5 груш, а слив на 7 деревьев больше, чем яблонь и груш вместе;
2. В саду росло 25 деревьев, из них 7 были яблони и столько же груш;
3. В саду росло 2 ряда грушевых деревьев по 5 в каждом, и 1 ряд яблонь, состоящий из 6 деревьев. Из-за вредоносных насекомых пришлось срубить 8 деревьев.
Учащиеся могут предложить следующие вопросы:
1. Сколько слив росло в саду? 2. Сколько всего деревьев в саду? 3. Сколько деревьев осталось в саду?
Слайд 20
3.Составление условия задачи по данному вопросу.
Цель: обобщить знания
о связях между данными и искомым.
При выполнении
таких упражнений учащиеся устанавливают, какие данные надо иметь, чтобы найти искомое.Например, учащимся предлагается составить условие задачи к вопросу: «Сколько ведер воды в двух бочках?». Дети устанавливают
- что в условии может быть дано число ведер воды в каждой бочке
- число ведер воды в одной из бочек и разность
- отношение между числом ведер в первой и второй бочках и т.п.
Слайд 22
1 этап
«Катя, Лена и Наташа купили по 4
тетради каждая, а Петя купил 8 тетрадей. Сколько всего
тетрадей купили ребята?»- Как мы решим задачу, если вопрос изменится на такой: (на доске) «На сколько больше тетрадей у девочек вместе, чем у Пети?
- Как мы решим задачу, если в её условие внесем следующие изменения: «Катя и Лена купили по 4 тетради каждая, а Петя и Наташа купили 8 тетрадей каждый. Сколько всего тетрадей купили ребята?»
Слайд 24
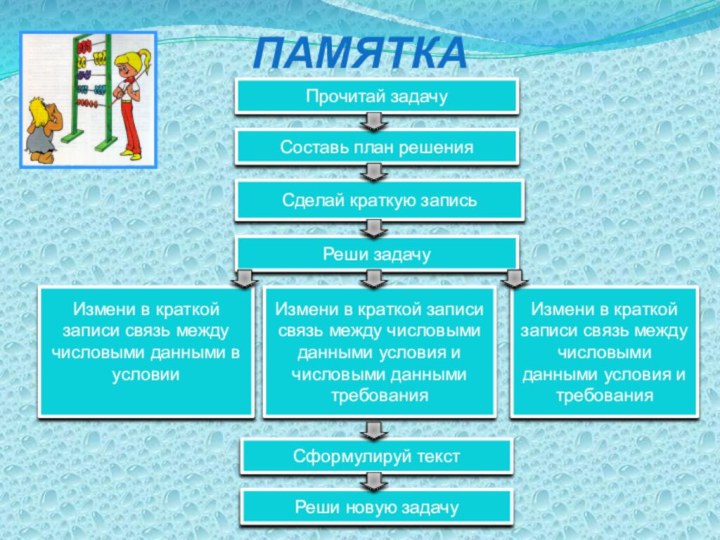
ПАМЯТКА
Прочитай задачу
Составь план решения
Реши задачу
Сделай краткую запись
Сформулируй текст
Реши
новую задачу
Измени в краткой записи связь между числовыми данными
условия и требования
Измени в краткой записи связь между числовыми данными условия и числовыми данными требования
Измени в краткой записи связь между числовыми данными в условии
Слайд 25
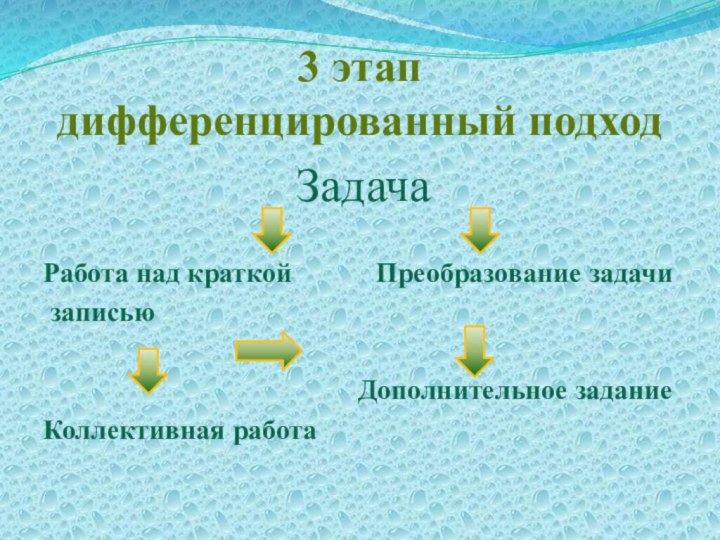
3 этап
дифференцированный подход
Задача
Работа над краткой
Преобразование задачи
записью
Дополнительное задание
Коллективная работа
Слайд 26
Деятельность учащихся
Выделяют задачи из предложенных текстов
Моделируют с помощью
предметов, рисунков, схематических рисунков
Объясняют и обосновывают действия, выбранные для
решения задачДополняют условия задачи недостающими данными или вопросом
Составляют и решают практические задачи с жизненными сюжетами
Наблюдают и объясняют как связаны между собой задачи
Составляют план решения
Работают в группах: распределяют виды работ между членами групп, устанавливают сроки выполнения работы по этапам и в целом, оценивают результаты работы.
Обнаруживают и устраняют логические ошибки и ошибки в вычислениях при решении задачи.
Отмечают изменения в решении задачи при изменении её условия или вопроса, проводят сбор информации
Находят различные способы решения одной и той же задачи
Выполняют прикидку результата





























