действий (УУД) у детей. УНИВЕРСАЛЬНЫЕ УЧЕБНЫЕ ДЕЙСТВИЯ – «центр
тяжести стандарта»личностные;
регулятивные;
познавательные;
коммуникативные
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Моделирование в начальной школе как средство формирования метапредметных умений.
Содержание
- 2. Младший школьный возраст является началом формирования
- 4. Познавательные УУД включают следующие действия: исследование,
- 5. Основное содержание оценки метапредметных результатов в начальной
- 6. МоделированиеМоделирование – это действие, которое выносится за
- 7. Для чего же младшим школьникам необходимо овладеть
- 8. Модель – это схема какого-нибудь
- 9. В зависимости от степени материальности, модели делятся
- 10. Выделяют четыре этапа моделирования: Вычленение
- 11. Умение учащихся работать с моделью, ее
- 12. Математика 1 класс Т.Е.Демидова С.А.Козлова А.П.Тонких
- 13. Математика 1 класс Т.Е.Демидова С.А.Козлова А.П.Тонких
- 14. Рассмотрим разные виды моделей в начальной школе. Модель-рисунок - реальный рисунок.Предметный рисунокСхематический рисунок
- 15. Математика 1 класс Т.Е.Демидова С.А.Козлова А.П.Тонких
- 16. Математика 1 класс Т.Е.Демидова С.А.Козлова А.П.Тонких
- 17. Математика 1 класс Т.Е.Демидова
- 18. Модель- схема сюжетной задачи помогает понять
- 19. Графическая модель –схема -это рисунки и чертежи,
- 20. Модель-схема является наиболее предпочтительной моделью при
- 21. Схематическая модель – это
- 22. Таблица- это вид модели
- 23. Данная табличная модель служит формой фиксации анализа
- 24. Одним из наиболее эффективных для формирования действия
- 25. Решение любой текстовой задачи состоит из
- 26. Основная цель ученика на первом этапе –
- 27. Решение задач:Цель ученика на втором этапе –
- 29. !!! Описанный обобщенный прием моделирования
- 30. Русский язык
- 31. Русский язык
- 32. Литературное чтение
- 33. Литературное чтение
- 34. Окружающий мир
- 35. Окружающий мир
- 36. Окружающий мир
- 37. Основы православной культуры
- 38. Технология
- 39. О Б Ж
- 40. Планируемые результаты:три основные группы результатовПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ: начальная
- 41. Метапредметные результаты:Умение освоить лексическое значение слов - математических понятий.
- 43. Метапредметные результаты: Умение знать разные способы получения информации.
- 45. Метапредметные результаты: Умение рассуждать, при решении текстовых математических задач.
- 47. Метапредметные результаты: Умение использовать знаково-символические средства
- 48. Метапредметные результаты: Умение использовать знаково-символические средства
- 49. Овладение основами алгоритмического мышления
- 50. Метапредметные результаты: Уметь выдвигать гипотезы и их обосновывать.
- 51. Скачать презентацию
- 52. Похожие презентации
Младший школьный возраст является началом формирования универсальных учебных действий (УУД) у детей. УНИВЕРСАЛЬНЫЕ УЧЕБНЫЕ ДЕЙСТВИЯ – «центр тяжести стандарта» личностные;регулятивные;познавательные;коммуникативные
Слайд 2 Младший школьный возраст является началом формирования универсальных учебных
Слайд 3 Под
метапредметными результатами в стандарте понимаются универсальные способы
деятельности:познавательные
коммуникативные
регулятивные
Слайд 4
Познавательные УУД включают следующие действия:
исследование,
поиск и отбор необходимой информации, ее структурирование;
моделирование
изучаемого содержания, логические действия и операции.
Слайд 5
Основное содержание оценки метапредметных результатов в начальной школе
строится вокруг умения учиться – совокупности способов действий, обеспечивающих
способность обучающихся к самостоятельному усвоению новых знаний и умений.
Слайд 6
Моделирование
Моделирование – это действие, которое выносится за пределы
младшего школьного возраста в дальнейшие виды деятельности человека и
выходит на новый уровень своего развития.С помощью моделирования можно свести изучение от простого, незнакомого - к знакомому , то есть сделать объект доступным для тщательного изучения.
Слайд 7 Для чего же младшим школьникам необходимо овладеть методом
моделирования?
Введение в содержание обучения понятий модели и моделирования существенно
меняет отношение учащихся к учебному процессу.Делает учебную деятельность осмысленной и более репродуктивной.
Целенаправленное и систематическое обучение методу моделирования приближает младших школьников к методам научного познания, обеспечивает их интеллектуальное развитие.
Слайд 8 Модель – это схема какого-нибудь физического объекта или
явления. Для того чтобы вооружить учащихся моделированием как способом
познания, нужно, чтобы школьники сами строили модели, сами изучали какие- либо объекты , явления с помощью моделирования.Слайд 9 В зависимости от степени материальности, модели делятся на
предметные и идеальные.
моделипредметные идеальные
глобус, модель термометра, машина
образные знаковые мысленные схемы, графики, рисунки символы и знаки-географ. карта абстрактные представления
Слайд 10
Выделяют четыре этапа моделирования:
Вычленение существенных признаков объекта.
Построение модели.
Исследование модели.
Перенос полученных на моделях сведений
на изучаемый объект. Особенность моделирования состоит в том, что наглядность представляет собой не простое демонстрирование натуральных объектов, а стимулирует самостоятельную практическую деятельность детей.
Слайд 11 Умение учащихся работать с моделью, ее преобразование для
изучения общих свойств изучаемых понятий составляет одну из главных
задач обучения во всех предметных областях.модель – это предмет, уменьшенная копия настоящего объекта
Слайд 12 Математика 1 класс Т.Е.Демидова С.А.Козлова А.П.Тонких стр. 13 –
1часть. На начальном этапе обучения моделированию упражняемся в сравнении,
обобщении объектов одного класса.Слайд 13 Математика 1 класс Т.Е.Демидова С.А.Козлова А.П.Тонких стр. 19 –
1часть. Учащиеся учатся распознавать признаки сходства и различия, выделять главные,
по которым несколько объектов можно объединить в одну группу.Слайд 14 Рассмотрим разные виды моделей в начальной школе. Модель-рисунок
- реальный рисунок.
Предметный рисунок
Схематический рисунок
Слайд 15 Математика 1 класс Т.Е.Демидова С.А.Козлова А.П.Тонких стр. 17 –
2 часть.
Условные предметы в виде геометрических фигур.
Слайд 16 Математика 1 класс Т.Е.Демидова С.А.Козлова А.П.Тонких стр. 13 –
2 часть.
Незаметно переходим к схемам.
Слайд 17 Математика 1 класс Т.Е.Демидова С.А.Козлова А.П.Тонких
стр. 23 – 2 часть. Символические рисунки играют
роль переходного мостика от конкретно-образного к абстрактному мышлению, а также позволяют сделать процесс моделирования конкретным и наглядным.Слайд 18 Модель- схема сюжетной задачи помогает понять учащимся абстрактные
отношения , заданные в условии задачи , в конкретной
пространственной форме. Математика 1 класс Т.Е.Демидова С.А.Козлова А.П.Тонких стр. 49 – 1 часть.
Слайд 19 Графическая модель –схема -это рисунки и чертежи, которые
помогают понять задачу, организовать поиск её решения. Графическая модель
– наиболее удачная опора для построения мысленной модели задачи: с одной стороны, она достаточно конкретна, воспринимаема зрительно, с другой – полностью отражает внутренние связи и количественные соотношения задач.«В куске было 10 м ткани. Одному покупателю продали 5 м, а другому 2 м. Сколько метров ткани осталось в куске?»
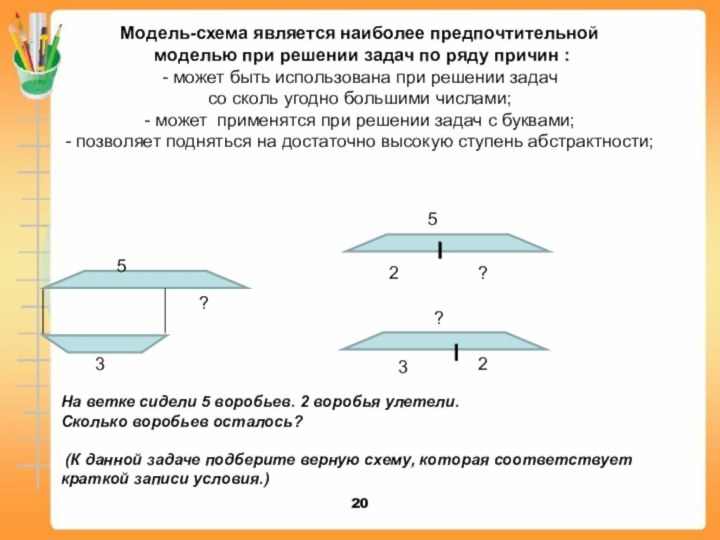
Слайд 20 Модель-схема является наиболее предпочтительной моделью при решении задач
по ряду причин : - может быть использована при
решении задач со сколь угодно большими числами; - может применятся при решении задач с буквами; - позволяет подняться на достаточно высокую ступень абстрактности;5
?
5
2
?
?
3
2
На ветке сидели 5 воробьев. 2 воробья улетели.
Сколько воробьев осталось?
(К данной задаче подберите верную схему, которая соответствует краткой записи условия.)
3
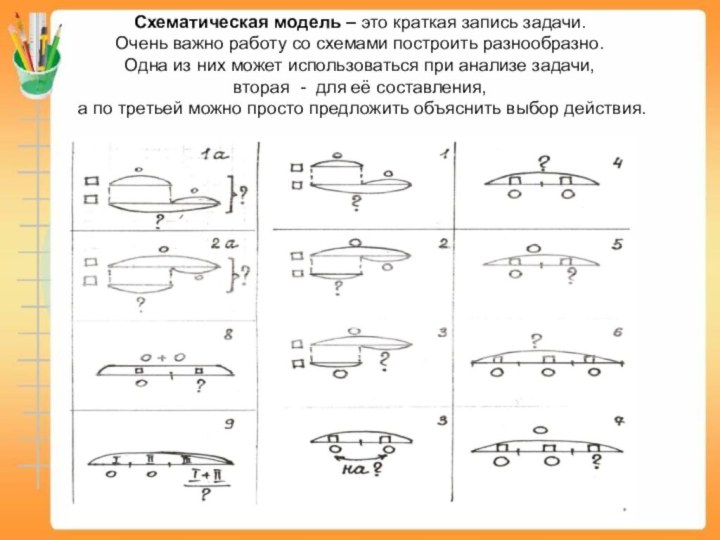
Слайд 21 Схематическая модель – это краткая запись задачи. Очень
важно работу со схемами построить разнообразно. Одна из них
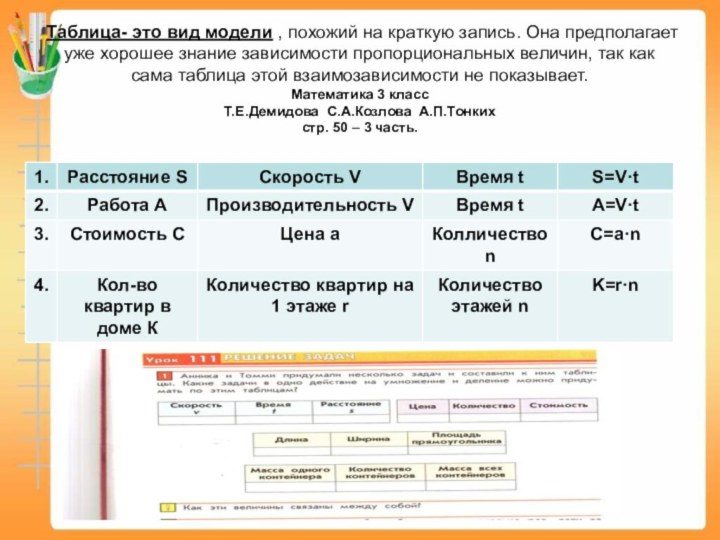
может использоваться при анализе задачи, вторая - для её составления, а по третьей можно просто предложить объяснить выбор действия.Слайд 22 Таблица- это вид модели , похожий на краткую
запись. Она предполагает уже хорошее знание зависимости пропорциональных величин,
так как сама таблица этой взаимозависимости не показывает. Математика 3 класс Т.Е.Демидова С.А.Козлова А.П.Тонких стр. 50 – 3 часть.Слайд 23 Данная табличная модель служит формой фиксации анализа сюжетной
задачи и является основным средством поиска решения. Пользуясь такой
схемой, нетрудно найти план и осуществить решение задачи.Слайд 24 Одним из наиболее эффективных для формирования действия моделирования
типов заданий являются текстовые задачи .
Этапы решения задачи.
Знаково-символическая модель
Мысленная
модельСловесная модель
Слайд 25
Решение любой текстовой задачи
состоит из нескольких этапов:
Восприятие
и анализ текста задачи;
Перевод текста на язык математики с
помощью вербальных и невербальных средств-моделей различного вида: чертежи, схемы, таблицы, формулы, уравнения…Установление отношений между данными и вопросом. Выделяется 4 типа отношений между объектами и их величинами: равенство, часть/целое, разность, кратность,-сочетание которых определяет разнообразие способов решения задач.
Составление плана решения;
Выполнение решения и получение ответа на вопрос задачи;
Проверка и оценка решения задач;
Слайд 26 Основная цель ученика на первом этапе – это
понять задачу. Ученик должен чётко представить себе: о чём
эта задача? Что в задаче известно? Что нужно найти? Как связаны между собой данные (числа, величины, значения величин)? Какими отношениями связаны данные и неизвестные, данные и искомое? Что является искомым: число, отношение, некоторое утверждение?
Слайд 27
Решение задач:
Цель ученика на втором этапе – выделить
величины, данные и искомые числа, входящие в задачу, установить
связи между данными и искомым и на этой основе выбрать соответствующие арифметические действия – решение.Использование различных методических приёмов при обучении решению простых задач способствует развитию кругозора учащихся, правильному пониманию математического смысла различных жизненных ситуаций, активизирует их познавательную активность. На данном этапе можно использовать различные способы моделирования.
Выбрав арифметическое действие, учащиеся переходят к его выполнению, т. е. к третьему этапу решения задачи.
Четвёртый этап - проверка решённой задачи.
Слайд 29 !!! Описанный обобщенный прием моделирования при
решении задач применительно к математике
в своей общей структуре может быть перенесен на любой учебный предмет.
Слайд 40
Планируемые результаты:
три основные группы результатов
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ: начальная школа
ЛИЧНОСТНЫЕ
МЕТАПРЕДМЕТНЫЕ
ПРЕДМЕТНЫЕ
Самоопределение:
внутренняя
позиция школьника;
самоиндификация;
самоуважение и самооценка
Смыслообразование:
мотивация (учебная, социальная);
границы собственного
знания и «незнания»
Морально-этическая
ориентация:
ориентация
на выполнениеморальных норм;
способность к решению моральных
проблем на основе децентрации;
оценка своих поступков
Регулятивные:
управление своей деятельностью;
контроль и коррекция;
инициативность и самостоятельность
Коммуникативные:
речевая деятельность;
навыки сотрудничества
Познавательные:
работа с информацией;
работа с учебными моделями;
использование знако-символических
средств, общих схем решения;
выполнение логических операций
сравнения, анализа, обобщения,
классификации, установления
аналогий, подведения под понятие
Основы системы
научных знаний
Опыт «предметной» деятельности по получению,
преобразованию
и применению
нового знания
РЯ
ЛЧт
ИЯ
Мат
ОМ
Муз
ИЗО
Тех
Физ
Предметные и метапредметные действия с учебным материалом
Слайд 41
Метапредметные результаты:
Умение освоить
лексическое значение слов -
математических понятий.
Слайд 42
Метапредметные результаты:
Умение: наблюдать,
сравнивать, анализировать, моделировать, классифицировать, устанавливать аналогии.,
Слайд 44
Метапредметные результаты:
Сформировать
умение вести диалог на заданную тему, применять правила речевого этикета.
Слайд 46
Метапредметные результаты:
Умение на примере практических ситуаций строить логические суждения и делать умозаключения.Слайд 47 Метапредметные результаты: Умение использовать знаково-символические средства для создания моделей
изучаемых объектов и процессов, для создания схем решения учебно-познавательных
и практических задач.Слайд 48 Метапредметные результаты: Умение использовать знаково-символические средства для создания
моделей изучаемых объектов и процессов, для создания схем решения
учебно-познавательных и практических задач,S
S
t
V
t
V
Расстояние -
Время -
Скорость -
Слайд 49
Овладение основами алгоритмического мышления
Метапредметные результаты:
Овладение основами пространственного воображения.
(3 класс, 1 ч.)
