- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Формирование умения решать уравнения в начальной школе
Содержание
- 2. АктуальностьАктуальность исследования: Уравнения в школьном курсе алгебры
- 3. Основные понятия:Уравнение – математическое равенство с одной
- 4. Программа по математике для начальной школы по учебнику Н.Б. Истомина
- 5. Пояснительная записка:Специальная тема в IV классе посвящена
- 6. Программа 4 класса (136ч)Уравнения. Способы решения уравнений (простых и усложненных). Решение задач способом составления уравнений.
- 7. Обучающиеся 4 класса должны уметь:Решать простые и
- 8. Программа по математике для начальной школы по учебнику И.И. Аргинская
- 9. Пояснительная запискаВходит знакомство с буквенными выражениями, неравенства
- 10. Содержание программы 1 кл. Изучение элементов алгебрыРешение
- 11. Требование к уровню подготовки обучающихся к концу
- 12. Содержание программы 2 кл.Изучение действий:Сложение и вычитание:Решение
- 13. Требования к уровню подготовки обучающихся к концу
- 14. Содержание программы 3 кл.Изучение элементов алгебры:Решение неравенств
- 15. Содержание программы 4 кл.Изучение элементов алгебры:Свойства равенств
- 16. Историческая справкаГреция. Первые сокращенные обозначения для неизвестных
- 17. Программа по математике для начальной школы по учебнику И. И. Аргинская
- 18. Не выполняя вычислений, найди корень
- 19. Не выполняя вычислений, найди корень уравнений:
- 20. Верно ли утверждение, что корни уравнений в
- 21. Скачать презентацию
- 22. Похожие презентации
АктуальностьАктуальность исследования: Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее


















Слайд 3
Основные понятия:
Уравнение – математическое равенство с одной или
несколькими неизвестными величинами, верное только при определенных значениях этих
величин.Уравнение – равенство двух буквенных выражений, для которого ставится задача отыскать все значения переменных, при которых значения данных выражений равны. Переменные, входящие в уравнение, называются неизвестными.
Уравнение – это два выражения, соединенные знаком равенства; в эти выражения входят одна или несколько переменных, называемых неизвестными.
Решить уравнение – значит найти все значения неизвестных, при которых оно обращает в верное равенство, или установить, что таких значений нет.
Слайд 5
Пояснительная записка:
Специальная тема в IV классе посвящена решению
уравнений как простых и усложненных.В этой же теме учащимся
разъясняется алгебраический способ решения задач. В конце 4 класса обучающиеся знакомятся с буквенными выражениями. Отнесение тем «Уравнения» и «Буквенные выражения» на конец 4 класса позволяет обобщить тот материал, который изучался в 1-4 классах.
Слайд 6
Программа 4 класса (136ч)
Уравнения. Способы решения уравнений (простых
и усложненных). Решение задач способом составления уравнений.
Слайд 7
Обучающиеся 4 класса должны уметь:
Решать простые и усложненные
уравнения на основе правил нахождения неизвестного компонента. Решение задач
способом составления уравнений.
Слайд 9
Пояснительная записка
Входит знакомство с буквенными выражениями, неравенства и
уравнения, а также наблюдения за изменением результата изученных арифметических
действий при изменении одного или обоих компонентов этих действий.В третьем классе большую роль в осознании связи между обратными действиями играет знакомство с уравнениями, их решение на основе этих взаимосвязей, которые начинаются в 1 классе и продолжаются до конца обучения в начальной школе.
Слайд 10
Содержание программы 1 кл.
Изучение элементов алгебры
Решение уравнения вида
х + а = в, а – х =
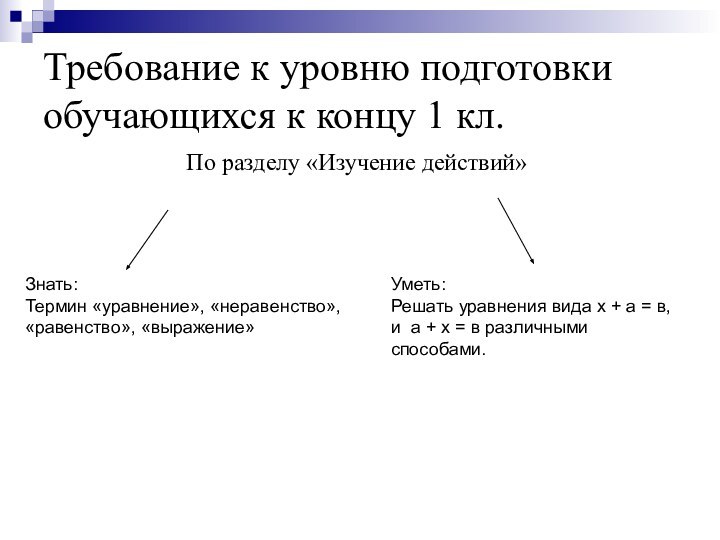
в, х – а = в различными способами(подбором , движением по натуральному ряду, с помощью таблицы сложения, на основе связи между сложением и вычитанием).Слайд 11 Требование к уровню подготовки обучающихся к концу 1
кл.
По разделу «Изучение действий»
Знать:
Термин «уравнение», «неравенство»,
«равенство», «выражение»
Уметь:
Решать уравнения вида
х + а = в, и а + х = в различными способами.
Слайд 12
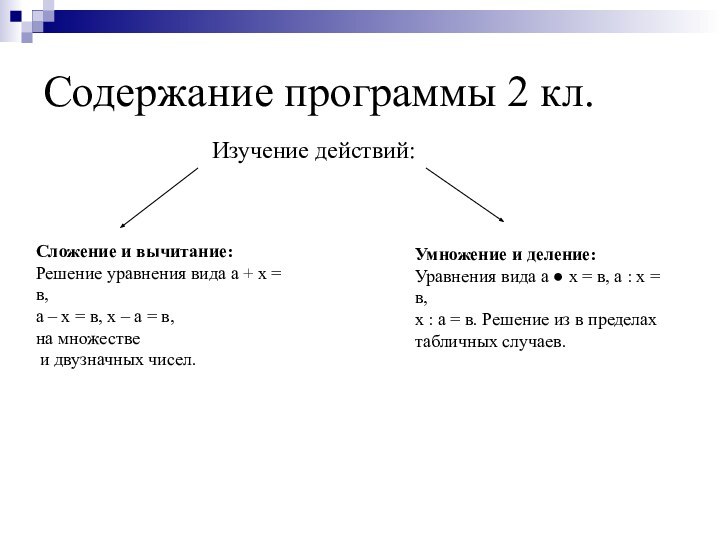
Содержание программы 2 кл.
Изучение действий:
Сложение и вычитание:
Решение уравнения
вида а + х = в,
а – х =
в, х – а = в, на множестве
и двузначных чисел.
Умножение и деление:
Уравнения вида а ● х = в, а : х = в,
х : а = в. Решение из в пределах
табличных случаев.
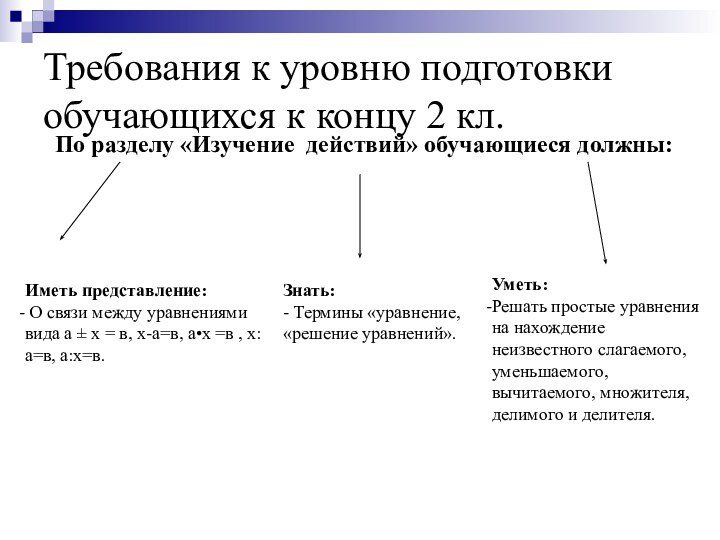
Слайд 13 Требования к уровню подготовки обучающихся к концу 2
кл.
По разделу «Изучение действий» обучающиеся должны:
Иметь представление:
О связи
между уравнениями вида а ± х = в, х-а=в, а•х =в , х:а=в, а:х=в. Знать:
- Термины «уравнение, «решение уравнений».
Уметь:
Решать простые уравнения на нахождение неизвестного слагаемого, уменьшаемого, вычитаемого, множителя, делимого и делителя.
Слайд 14
Содержание программы 3 кл.
Изучение элементов алгебры:
Решение неравенств вида
а ± х ) в, х – а )
в на основе соответствующих уравнений а ± х = в, х – а = в. Решение неравенств вида а • х <(>) в, а : х <(>)в, х :а <(>)в подбором и на основе соответствующих уравнений а • х = в, х : а = в. Знакомство с уравнениями вида а ± х ± в = с и другими такого же уровня сложности. Знакомство с уравнениями вида а • х ± в = с, (а ± в): х = с и другими такого же уровня сложности. Решение таких уравнений на основе использования изученных законов и свойств действий и взаимосвязи между их компонентами.
Слайд 15
Содержание программы 4 кл.
Изучение элементов алгебры:
Свойства равенств и
их использования для решения уравнений. Уравнения, содержащее неизвестное в
обеих частях. Решение таких уравнений. Системы уравнений. Решение их подбором. Знакомство с другими способами решения систем уравнений(простейшие случаи). Решение систем неравенств на основе решения соответствующих уравнений.
Слайд 16
Историческая справка
Греция. Первые сокращенные обозначения для неизвестных величин
встречаются у древнегреческого математика Диофанта (2-3 в.н.э.). Неизвестное Диофант
именует «аритмос» (число), вторую степень неизвестного – «дюнамис» (это слова имеет много значений: сила, могущество, имущество, степень и др.). Третью степень Диофант называет «кюбос» (куб), четвертую – «дюнамодюнамис», пятую – «дюнамокюбос», шестую – «кюбокюбос». Эти величины он обозначает первыми буквами соответствующих наименований (ар, дю, кю, ддю, дкю, ккю). Известные числа для отличия от неизвестных сопровождаются обозначением «мо» (монас – единица). Сложение не обозначается совсем, для вычитания имеется сокращенное обозначение, равенство обозначается «ис» (исос – равный).Ни вавилоняне, ни греки не рассматривали отрицательных чисел. Уравнение 3 ар 6 мо ис 2 ар 1 мо (3x+6=2x+1) Диофант называет «неуместным». Перенося члены из одной части уравнения в другую, Диофант говорит, что слагаемое становится вычитаемым, а вычитаемое – слагаемым.
Слайд 18
Не выполняя вычислений, найди корень уравнения:
а) 5000
+ 600 + x + 4 = 5674
б)4000
+ x + 30 + 2 = 4032
Слайд 19
Не выполняя вычислений, найди корень уравнений:
а)147 + 147
+ 147 + 147 + x = 147 •
5б) 3021 • 5 +3021 • 2 + 3021 = 3021 • x
Слайд 20 Верно ли утверждение, что корни уравнений в каждой
паре одинаковые?
а) x + (90 + 30) = 180
(x
+ 90) + 30 = 180б)(x + 70) + 25 = 814
x + (70 + 25) = 814.





























