- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Абсолютные и относительные величины в статистике
Содержание
- 2. § 1 Абсолютные величины
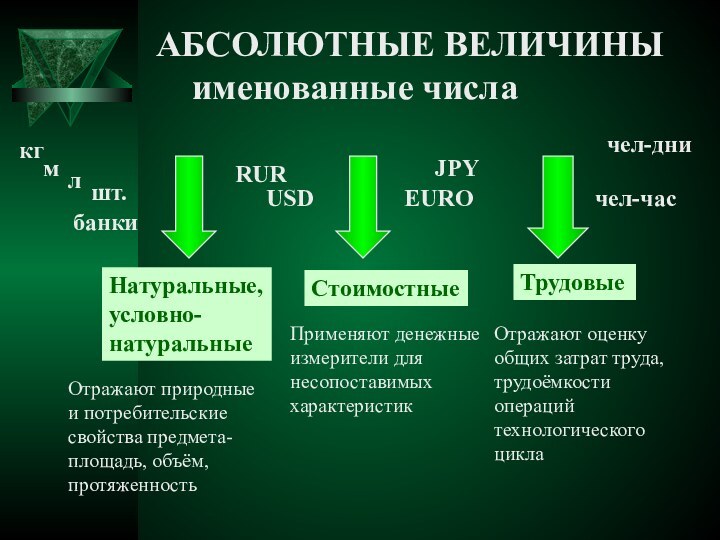
- 3. АБСОЛЮТНЫЕ ВЕЛИЧИНЫ именованные числа
- 4. ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА -ОБОБЩАЮЩАЯ ВЕЛИЧИНА, РЕЗУЛЬТАТ ОТ ДЕЛЕНИЯ, ЧИСЛОВАЯ МЕРА СООТНОШЕНИЯ МЕЖДУ ПОКАЗАТЕЛЯМИ§ 2 Относительные величины
- 5. ВИДЫ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН(ПОКАЗАТЕЛЕЙ):Относительный показатель структуры;Относительный показатель динамики;Относительный
- 6. ОПС =ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ ЧАСТЬ СОВОКУПНОСТИПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ СОВОКУПНОСТЬ В ЦЕЛОМОтносительный показательструктурыДоля или удельный вес
- 7. ОПД =ТЕКУЩИЙ ПОКАЗАТЕЛЬПРЕДШЕСТВУЮЩИЙ ИЛИ БАЗИСНЫЙ ПОКАЗАТЕЛЬОтносительный показательдинамики
- 8. ОПК =ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ i-Ю ЧАСТЬ СОВОКУПНОСТИПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ ЧАСТЬ СОВОКУПНОСТИ,ПРИНЯТУЮ ЗА БАЗУ СРАВНЕНИЯОтносительный показателькоординации
- 9. ОПСр =ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ СУБЪЕКТ АПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ СУБЪЕКТ ВОтносительный показательсравнения
- 10. ОПИ и ОПУЭР =ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ ЯВЛЕНИЕ АПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ СРЕДУ РАСПРОСТРАНЕНИЯ ЯВЛЕНИЯ АОтносительный показательинтенсивностиОтносительный показательуровня экономическогоразвития
- 11. ОПРП =ПОКАЗАТЕЛЬ, ДОСТИГНУТЫЙ В ИЗУЧАЕМОМ ПЕРИОДЕПОКАЗАТЕЛЬ, ЗАПЛАНИРОВАННЫЙ НА ИЗУЧАЕМЫЙ ПЕРИОДОтносительный показательреализации плана
- 12. ПРИМЕРЫ РАСЧЁТАОТНОСИТЕЛЬНЫХПОКАЗАТЕЛЕЙ
- 13. 1. Объёмы торгов ММВБ:09.07- 47,6 млн.USD10.07- 49,65 млн. USD,сравнить объёмы торговза изучаемые даты
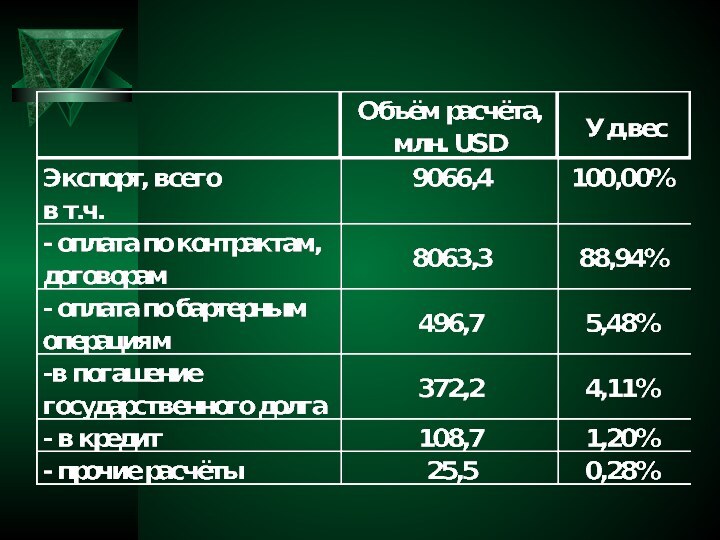
- 14. 2. По данным экспорта произвести оценку:
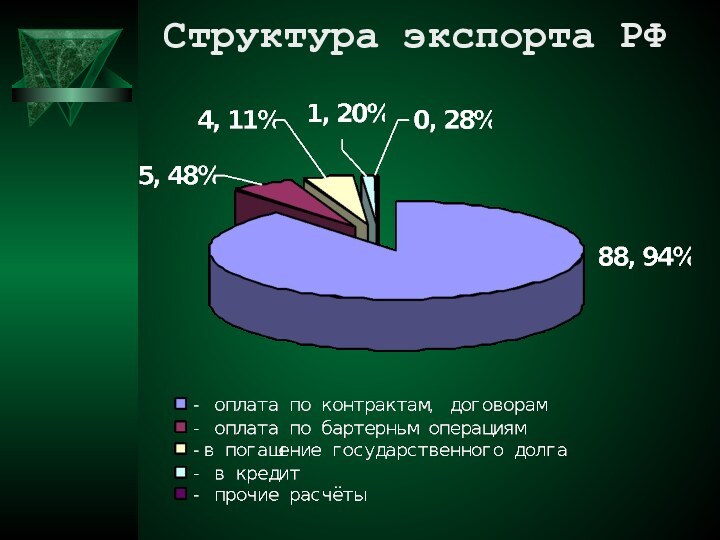
- 16. Структура экспорта РФ
- 17. 3. Найти соотношение оплат по контрактамк бартерным
- 18. 4. Цена на 1 кг картофеля в
- 19. 5. ВАЛОВОЙ ВНУТРЕННИЙ ПРОДУКТ (ВВП) В I
- 20. ВЫВОДЫ:АБСОЛЮТНЫЕ ПОКАЗАТЕЛИ В СТАТИСТИКЕ ИМЕЮТ ЕДИНИЦЫ ИЗМЕРЕНИЯ
- 21. ТЕМАСРЕДНИЕ ВЕЛИЧИНЫ В СТАТИСТИКЕ
- 22. § 1. ПОНЯТИЕ СРЕДНЕЙ ВЕЛИЧИНЫСРЕДНЯЯ ВЕЛИЧИНА В
- 23. Величины, в которых находят выражение общие условия,
- 24. Определяющее свойство средней
- 25. ИСС для некоторых экономических показателей1234
- 26. ВИДЫ СРЕДНИХ ВЕЛИЧИН В СТАТИСТИКЕСредняя арифметическая (простая,
- 27. Используется для расчёта среднего значения признака при известном объёме совокупности§ 2 СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЕЛИЧИНА
- 28. Средняя арифметическая простаяИспользуется для расчёта среднего значения признака при известныхиндивидуальных значениях признака(для несгруппированных данных)
- 29. Средняя арифметическая взвешеннаяИспользуется для расчёта среднего значения группировочногопризнака(для сгруппированных данных)
- 30. РЯДЫ РАСПРЕДЕЛЕНИЯ -конкретное значение признака в i- й группе
- 31. Средняя из групповыхсреднихИспользуется для расчёта среднего значения результативногопризнака( при сгруппированных данных)
- 32. Используется при неизвестном объёме совокупности или необходимости обобщениявеличины, обратной изучаемому признаку.§3. СРЕДНЯЯ ГАРМОНИЧЕСКАЯ
- 33. Средняя гармоническая
- 34. Используется для расчёта средних темпов и коэффициентов
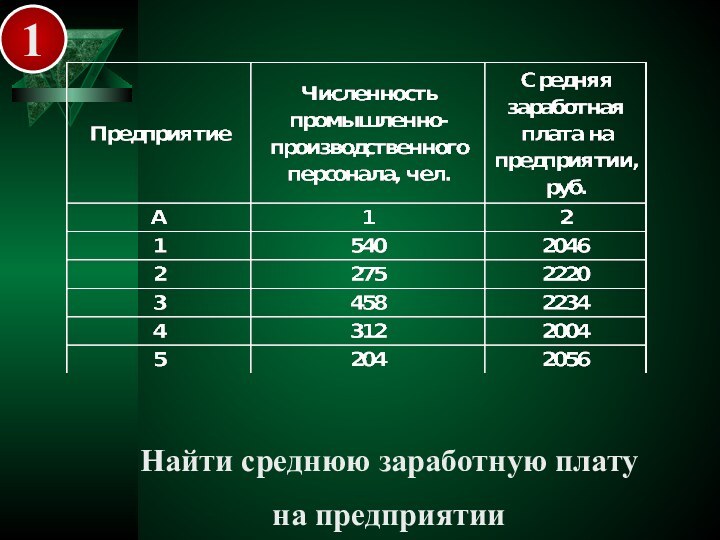
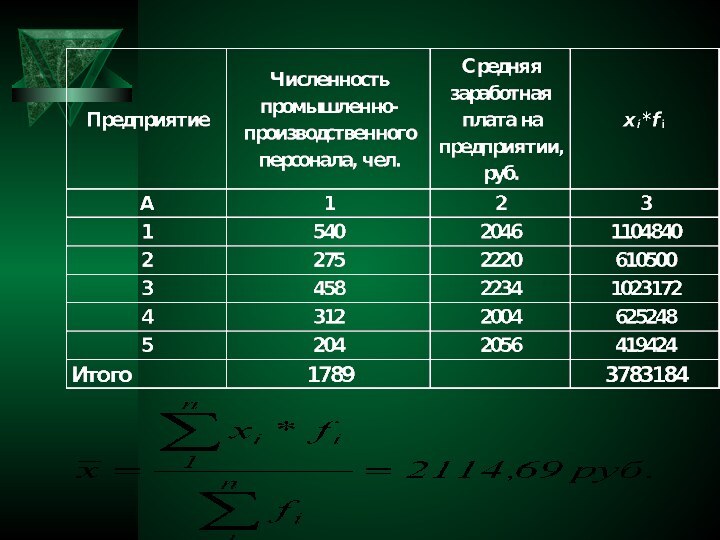
- 35. Примеры
- 36. 1
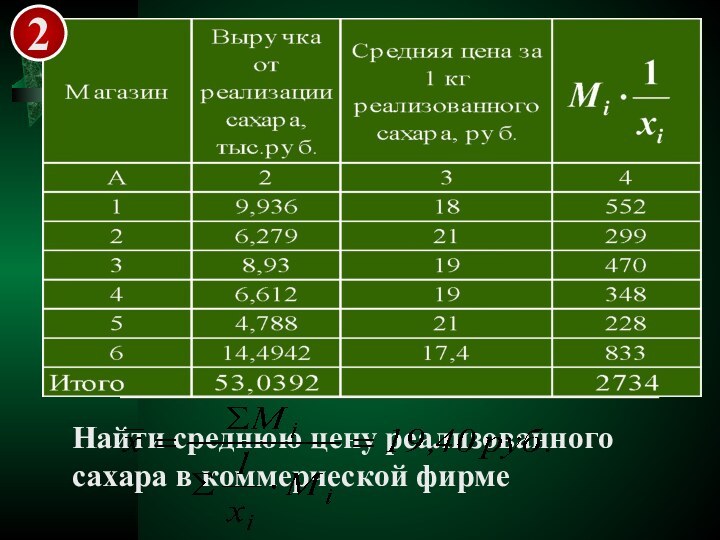
- 38. 2
- 40. Скачать презентацию
- 41. Похожие презентации
§ 1 Абсолютные величины
Слайд 4 ОТНОСИТЕЛЬНАЯ ВЕЛИЧИНА -ОБОБЩАЮЩАЯ ВЕЛИЧИНА, РЕЗУЛЬТАТ ОТ ДЕЛЕНИЯ, ЧИСЛОВАЯ
МЕРА СООТНОШЕНИЯ МЕЖДУ ПОКАЗАТЕЛЯМИ
Слайд 5
ВИДЫ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН
(ПОКАЗАТЕЛЕЙ):
Относительный показатель структуры;
Относительный показатель динамики;
Относительный показатель
координации;
Относительный показатель сравнения;
Относительный показатель интенсивности, уровня экономического развития;
Относительный показатель
реализации плана
Слайд 6
ОПС =
ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ ЧАСТЬ СОВОКУПНОСТИ
ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ СОВОКУПНОСТЬ В
ЦЕЛОМ
Относительный показатель
структуры
Доля или удельный вес
Слайд 7
ОПД =
ТЕКУЩИЙ ПОКАЗАТЕЛЬ
ПРЕДШЕСТВУЮЩИЙ ИЛИ БАЗИСНЫЙ ПОКАЗАТЕЛЬ
Относительный показатель
динамики
Слайд 8
ОПК =
ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ i-Ю ЧАСТЬ СОВОКУПНОСТИ
ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ ЧАСТЬ
СОВОКУПНОСТИ,
ПРИНЯТУЮ ЗА БАЗУ СРАВНЕНИЯ
Относительный показатель
координации
Слайд 9
ОПСр =
ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ СУБЪЕКТ А
ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ СУБЪЕКТ В
Относительный
показатель
сравнения
Слайд 10
ОПИ и ОПУЭР =
ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ ЯВЛЕНИЕ А
ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ
СРЕДУ
РАСПРОСТРАНЕНИЯ ЯВЛЕНИЯ А
Относительный показатель
интенсивности
Относительный показатель
уровня экономического
развития
Слайд 11
ОПРП =
ПОКАЗАТЕЛЬ, ДОСТИГНУТЫЙ В ИЗУЧАЕМОМ ПЕРИОДЕ
ПОКАЗАТЕЛЬ, ЗАПЛАНИРОВАННЫЙ НА
ИЗУЧАЕМЫЙ
ПЕРИОД
Относительный показатель
реализации плана
Слайд 13
1. Объёмы торгов ММВБ:
09.07- 47,6 млн.USD
10.07- 49,65 млн.
USD,
сравнить объёмы торгов
за изучаемые даты
Слайд 17
3. Найти соотношение оплат по контрактам
к бартерным операциям
в предыдущем
примере
Это означает, что на 1 млн.USD операций
поконтрактам приходится 61600 USD операций
по бартеру
Слайд 18
4. Цена на 1 кг картофеля в июле
текущего
года на рынках
города:
Первомайский рынок- 6 руб.
Первореченский рынок - 7
руб.Произвести оценку стоимости
картофеля
Слайд 19
5. ВАЛОВОЙ ВНУТРЕННИЙ
ПРОДУКТ (ВВП) В I квартале
текущего
года в России составил 96,1 млрд.руб.,
оценить уровень экономического
развития, если
известно, что численностьнаселения 145,6 млн. чел.:
Слайд 20
ВЫВОДЫ:
АБСОЛЮТНЫЕ ПОКАЗАТЕЛИ В СТАТИСТИКЕ
ИМЕЮТ ЕДИНИЦЫ ИЗМЕРЕНИЯ (КГ,
М, Л, ШТ.,
БАНКИ, РУБ., ЧЕЛ-ЧАС И Т.Д.)
ОТНОСИТЕЛЬНЫЕ ПОКАЗАТЕЛИ ИМЕЮТ
ЕДИНИЦАМИ ИЗМЕРЕНИЯ ЛИБО ПРОЦЕНТЫ
(ПРОМИЛЛЕ, ПРОДЕЦИМИЛЛЕ), ЛИБО НЕ
ИМЕЮТ ЕДИНИЦЫ ИЗМЕРЕНИЯ. ИСКЛЮЧЕНИЕМ
ЯВЛЯЮТСЯ ОПИ и ОПУЭР
АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ПОКАЗАТЕЛИ
НЕ ПРОТИВОРЕЧАТ ДРУГ ДРУГУ, ОПИСЫВАЯ
ИЗУЧАЕМОЕ ЯВЛЕНИЕ И ПРОЦЕСС И ДОПОЛНЯЮТ
ДРУГ ДРУГА
Слайд 22
§ 1. ПОНЯТИЕ СРЕДНЕЙ ВЕЛИЧИНЫ
СРЕДНЯЯ ВЕЛИЧИНА В СТАТИСТИКЕ-
ОБОБЩАЮЩИЙ ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ ТИПИЧНЫЙ УРОВЕНЬ ЯВЛЕНИЯ, СВОДНАЯ ХАРАКТЕРИСТИКА ЗАКОНОМЕРНОСТЕЙ
ТОГО ПРОЦЕССА, В КОТОРЫХ ОН ПРОТЕКАЕТ.Слайд 23 Величины, в которых находят выражение общие условия, закономерность
изучаемого явления;
Величины, отражающие то общее, что складывается в каждом
единичном объекте;Обобщённая количественная признака в статистической совокупности в конкретных условиях места и времени;
Является обобщением какого-то одного свойства изучаемого явления или процесса.
Слайд 26
ВИДЫ СРЕДНИХ ВЕЛИЧИН В СТАТИСТИКЕ
Средняя арифметическая (простая, взвешенная,
средняя из групповых средних);
Средняя гармоническая;
Средняя геометрическая;
Средняя квадратическая, кубическая и
т.д.;Структурные средние.
Слайд 27
Используется для расчёта среднего значения признака
при известном
объёме совокупности
§ 2 СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЕЛИЧИНА
Слайд 28
Средняя арифметическая
простая
Используется для расчёта среднего
значения признака
при известных
индивидуальных значениях признака
(для несгруппированных данных)
Слайд 29
Средняя арифметическая
взвешенная
Используется для расчёта среднего
значения группировочного
признака
(для
сгруппированных данных)
Слайд 31
Средняя из групповых
средних
Используется для расчёта среднего
значения результативного
признака
(
при сгруппированных данных)
Слайд 32
Используется при неизвестном объёме совокупности или необходимости обобщения
величины,
обратной
изучаемому признаку.
§3. СРЕДНЯЯ ГАРМОНИЧЕСКАЯ
Слайд 34
Используется для расчёта средних
темпов и коэффициентов роста
в
