Презентация на тему Корреляционно-регрессионный анализ

Содержание

2. 1. ПОНЯТИЕ ВЗАИМОСВЯЗЕЙ, ИХ ВИДЫ
3. ТИП СВЯЗИфункциональная (детерминированная) статистическая (стохастическая)
4. КОРРЕЛЯЦИОННАЯ СВЯЗЬформа причинной связи, при которой причина
5. прямаяобратнаяпрямолинейнаякриволинейнаямногофакторнаяоднофакторная
6. Методы выявления наличия связи, характера и направленияприведения параллельных данныхграфическийкорреляционно-регрессионный анализ
7. Задачи корреляционно-регрессионного анализа1. Измерить тесноту связи между
8. 2. ПАРНАЯ КОРРЕЛЯЦИЯ И РЕГРЕССИЯ
9. Основные виды уравнений парной регрессииỹ - теоретическое
10. С целью вычисления параметров a0, a1 применяют метод наименьших квадратов и решают систему уравнений
11. Значение параметров
12. Значение параметровпараметр а0 показывает усредненное влияние на
13. Тесноту и направление парной линейной корреляционной связи измеряют с помощью линейного коэффициента корреляции - r
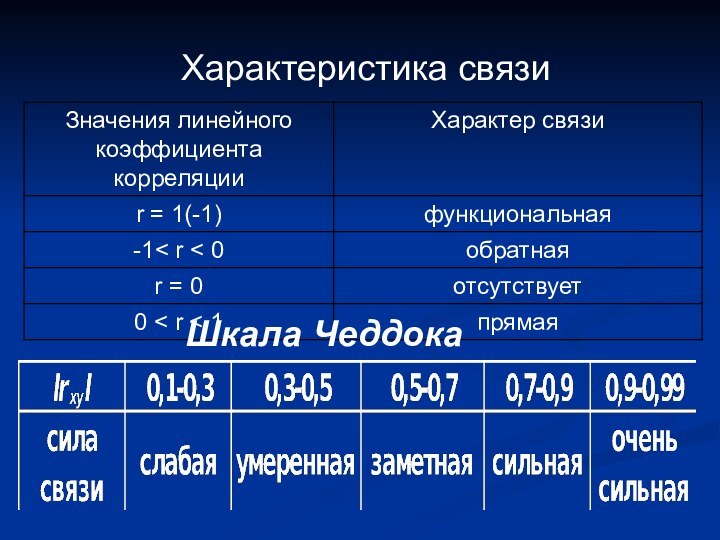
14. Характеристика связиШкала Чеддока
15. С целью оценки соответствия используемой регрессионной модели
16. адекватность регрессионной модели подтверждается еслиη = r
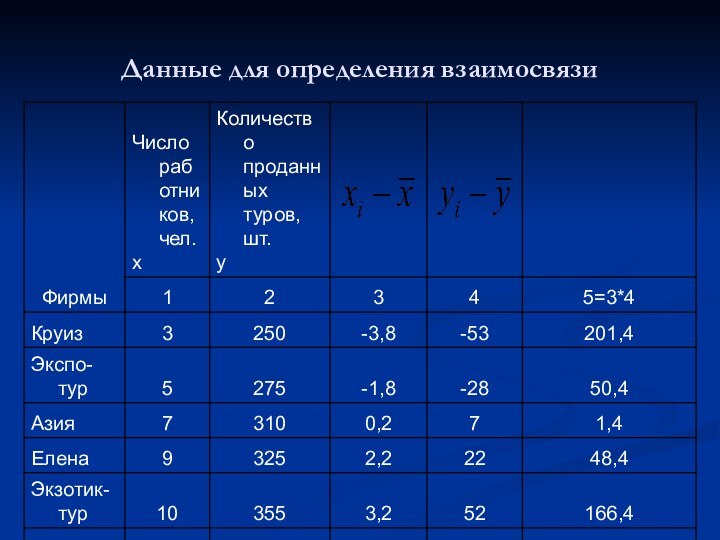
17. Данные для определения взаимосвязи
18. Данные для определения взаимосвязи
19. Значение = 34/5 =
20. уравнение регрессии примет вид = 205,98 + 14,27*х,
21. Далее, рассчитаем значение коэффициента корреляции = √32,8/5
22. Скачать презентацию
23. Похожие презентации

1. ПОНЯТИЕ ВЗАИМОСВЯЗЕЙ, ИХ ВИДЫ

Главная
Экономика
Корреляционно-регрессионный анализ

Кафедра «Бухгалтерский учет и аудит» Ослопова М.В. ТЕМА 8. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ

ТИП СВЯЗИфункциональная (детерминированная) статистическая (стохастическая)

КОРРЕЛЯЦИОННАЯ СВЯЗЬформа причинной связи, при которой причина определяет следствие не однозначно, а

прямаяобратнаяпрямолинейнаякриволинейнаямногофакторнаяоднофакторная

Методы выявления наличия связи, характера и направленияприведения параллельных данныхграфическийкорреляционно-регрессионный анализ

Задачи корреляционно-регрессионного анализа1. Измерить тесноту связи между результативным и факторным признаком. Задача

Основные виды уравнений парной регрессииỹ - теоретическое значение результативного признака а0 –

С целью вычисления параметров a0, a1 применяют метод наименьших квадратов и решают систему уравнений

Значение параметровпараметр а0 показывает усредненное влияние на результат неучтенных факторовпараметр a1 характеризует,

Тесноту и направление парной линейной корреляционной связи измеряют с помощью линейного коэффициента корреляции - r

С целью оценки соответствия используемой регрессионной модели фактическим данным, то есть ее

адекватность регрессионной модели подтверждается еслиη = r

уравнение регрессии примет вид = 205,98 + 14,27*х,

Далее, рассчитаем значение коэффициента корреляции = √32,8/5 = 2,56; = √ 6830/5

Далее, проверим адекватность используемой регрессионной модели, рассчитав значение корреляционного отношения η

Слайды презентации

Слайд 2 1. ПОНЯТИЕ ВЗАИМОСВЯЗЕЙ, ИХ ВИДЫ

Слайд 3 ТИП СВЯЗИ
функциональная
(детерминированная)

статистическая (стохастическая)

Слайд 4 КОРРЕЛЯЦИОННАЯ СВЯЗЬ
форма причинной связи,
при которой причина определяет

КОРРЕЛЯЦИОННАЯ СВЯЗЬформа причинной связи, при которой причина определяет следствие не однозначно,

следствие не однозначно, а лишь с определенной долей вероятности

Слайд 5 прямая
обратная
прямолинейная
криволинейная
многофакторная
однофакторная

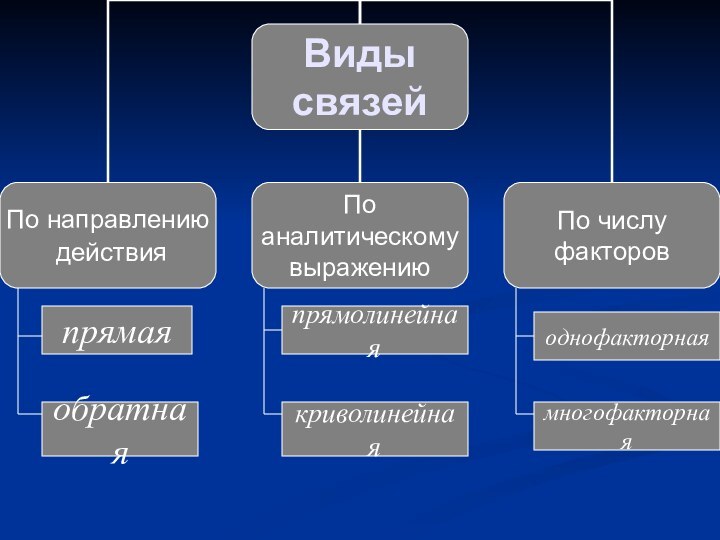
Слайд 6 Методы выявления наличия связи, характера и направления
приведения параллельных

данных

графический

корреляционно-регрессионный анализ

Слайд 7 Задачи корреляционно-регрессионного анализа
1. Измерить тесноту связи между результативным

Задачи корреляционно-регрессионного анализа1. Измерить тесноту связи между результативным и факторным признаком.

и факторным признаком. Задача решается путем вычисления корреляционного отношения,

коэффициента детерминации.

2. Оценить параметры уравнения регрессии, выражающего зависимость средних значений результативного признака от значений факторного признака. Задача решается путем вычисления коэффициентов регрессии.

3. Определить важнейшие факторы, влияющие на результативный признак. Задача решается путем оценки тесноты связи факторов с результатом.

4. Осуществить прогнозирование возможных значений результативного признака при задаваемых значениях факторных признаков. Задача решается путем подстановки ожидаемых значений факторов в регрессионное уравнение и вычисления прогнозируемых значений результата.