- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Чувствительность системы управления
Содержание
- 2. Чувствительность системы управления. В промышленных условиях
- 3. Чувствительность системы управления. Под чувствительностью понимается
- 4. Чувствительность системы управления. Количественно чувствительность системы
- 5. Чувствительность системы управления. где
- 6. Функции чувствительности временных характеристик Посредством этих функций чувствительности
- 7. Функции чувствительности временных характеристик Варьированной системой называют такую
- 8. Функции чувствительности временных характеристик Рассмотрим мгновенные вариации параметров
- 9. Функции чувствительности временных характеристик При условии дифференцируемости
- 10. Функции чувствительности временных характеристик Таким образом, первое приближение
- 11. Функции чувствительности временных характеристик Дифференцирование исходных уравнений (4)
- 12. Функции чувствительности временных характеристик где aik и biq
- 13. Функции чувствительности временных характеристик Уравнениям (9) соответствуют начальные
- 14. Функции чувствительности временных характеристик Для нахождения функции чувствительности
- 15. Функции чувствительности временных характеристик Здесь введена функция чувствительности
- 16. Функции чувствительности временных характеристик Может также использоваться так
- 17. Функции чувствительности временных характеристик Найдём дополнительную передаточную функцию
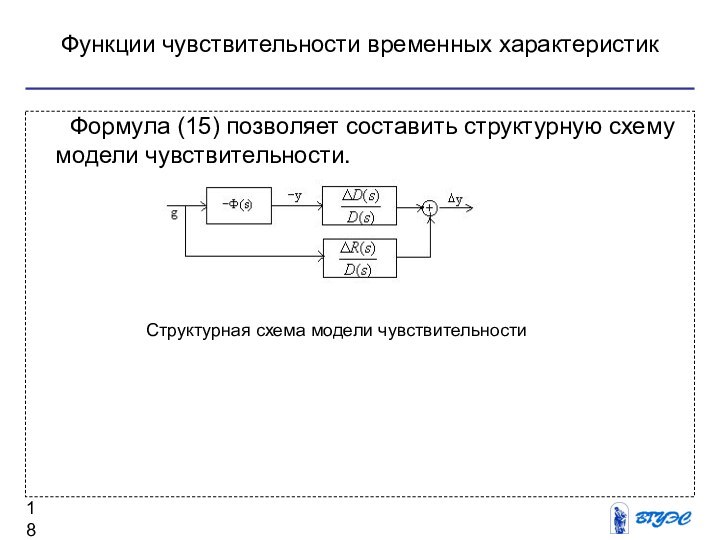
- 18. Функции чувствительности временных характеристик Формула (15) позволяет составить структурную схему модели чувствительности.Структурная схема модели чувствительности
- 19. Функции чувствительности временных характеристик Составим, например, модель чувствительности
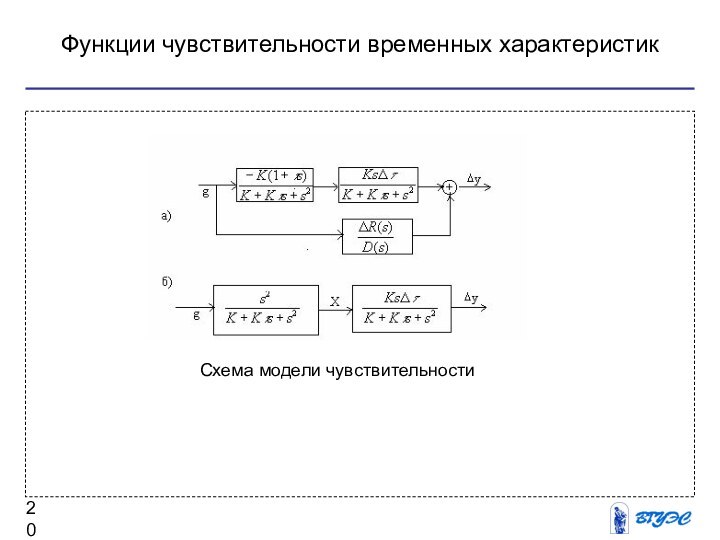
- 20. Функции чувствительности временных характеристик Схема модели чувствительности
- 21. Функции чувствительности временных характеристик Одной из важнейших характеристик
- 22. Функции чувствительности временных характеристик
- 23. Функции чувствительности критериев качестваЕсли в системе произошли
- 24. Функции чувствительности критериев качества Так как в большинстве
- 25. Функции чувствительности критериев качества Если заданы дисперсии отклонения
- 26. ПримерПусть передаточная функция разомкнутой системы имеет вид: Требуется
- 27. ПримерИсследование на максимум даёт:при КТ2Функции чувствительности, если
- 28. Контрольные вопросыКаков физический смысл чувствительности?Какова математическая интерпретация
- 29. Рекомендуемая литератураКривошеев В.П. Основы теории управления: Конспект
- 30. Скачать презентацию
- 31. Похожие презентации
Чувствительность системы управления. В промышленных условиях из-за ряда причин (изменение температуры, износ оборудования, снижение активности катализатора, снижение теплопроводности и т.п.) параметры системы управления постепенно изменяются, и их действительные значения всегда отличаются от расчётных. Влияние вариаций




























Слайд 3
Чувствительность системы управления.
Под чувствительностью понимается свойство системы
изменять свои выходные характеристики (показатели качества) при отклонении тех
или иных параметров от своих номинальных (расчётных) значений.Для обозначения противоположного свойства пользуются термином грубость, или робастность. Системы, сохраняющие свои свойства при любых параметрических возмущениях, называют грубыми, или робастными.
Слайд 4
Чувствительность системы управления.
Количественно чувствительность системы управления оценивается
с помощью функций чувствительности. Функции чувствительности представляют собой частные
производные i-й координаты системы по j-му параметру:, u =1,2,... (1)
или частные производные от используемого критерия качества по j-му параметру:
u =1,2,..., (2)
Слайд 5
Чувствительность системы управления.
где порядок функции
чувствительности;
0 индекс, обозначающий номинальный режим, относительно
которого определяется функция чувствительности.Наибольшее распространение получили функции чувствительности 1-го порядка.
Слайд 6
Функции чувствительности временных характеристик
Посредством этих функций чувствительности оценивается
влияние малых отклонений параметров системы от расчётных значений на
временные характеристики системы управления (переходную функцию, функцию веса и др.).Исходной системой называют систему, у которой все параметры равны расчётным значениям и не имеют вариаций. Этой системе соответствует так называемое основное движение.
Слайд 7
Функции чувствительности временных характеристик
Варьированной системой называют такую систему,
у которой произошли вариации параметров. Движение её называют варьированным
движением.Дополнительным движением называют разность между варьированным и основным движением.
Пусть исходная система описывается совокупностью нелинейных уравнений первого порядка:
(i=1, ..., n) (3)
Слайд 8
Функции чувствительности временных характеристик
Рассмотрим мгновенные вариации параметров так,
чтобы параметры приняли значения . Если изменения параметров не
вызывают изменения порядка дифференциального уравнения, то варьирование движения будет описываться совокупностью уравнений:(i=1, ..., n) (4)
Для дополнительного движения можно записать:
(5)
Слайд 9
Функции чувствительности временных характеристик
При условии дифференцируемости
и по параметрам
дополнительное движение можно разложить в ряд Тейлора.Для малых вариаций параметров допустимо ограничиться линейными членами разложения. Тогда получим уравнение первого приближения для дополнительного движения:
(6)
Частные производные, находящиеся в скобках, берутся при значениях переменных, соответствующих основному движению (то есть при =0).
Слайд 10
Функции чувствительности временных характеристик
Таким образом, первое приближение для
дополнительного движения может быть найдено при известных функциях чувствительности.
Заметим,
что использование функций чувствительности удобнее для нахождения дополнительного движения по сравнению с прямой формулой (5), так как последняя во многих случаях может дать большие ошибки вследствие необходимости вычитать две близкие величины.При значительных вариациях может оказаться необходимым использование второго приближения с удержанием в ряде Тейлора как линейных, так и квадратичных членов.
Слайд 11
Функции чувствительности временных характеристик
Дифференцирование исходных уравнений (4) по
приводит к уравнениям чувствительности:
(7)
i=1,2,...,n; j=1,2,...,m.
Решение этих уравнений
даёт функции чувствительности Uij.Обратимся теперь к линейным системам. Пусть система описывается совокупностью уравнений первого порядка:
(i=1,2,...,n), (8)
Слайд 12
Функции чувствительности временных характеристик
где aik и biq
постоянные коэффициенты, xi фазовые координаты, а fq(t)
внешнее воздействия. Начальные условия в системе: при t=0 . Уравнения чувствительности получаются из (8) дифференцированием по варьируемому параметру , от которого могут зависеть коэффициенты aik и biq:(i=1,2,...,n), (9)
частные производные от коэффициентов системы уравнений (8) по варьируемому параметру .
Слайд 13
Функции чувствительности временных характеристик
Уравнениям (9) соответствуют начальные условия:
(i=1,2,...,n).
Если
начальные условия не зависят от
параметра , то уравнениям (9) соответствуют начальные нулевые условия.Для решения (9) необходимо предварительно решить совокупность уравнений (8) и определить исходное движение (i=1,...,n).
Слайд 14
Функции чувствительности временных характеристик
Для нахождения функции чувствительности и
дополнительного движения удобно использовать передаточные функции системы. Пусть, например,
регулируемая величина y(t, ) связана с задающим воздействием зависимостью:(10)
где G(s) изображение задающего воздействия.
Функция чувствительности может быть получена из (10) его дифференцированием по параметру :
(11)
Слайд 15
Функции чувствительности временных характеристик
Здесь введена функция чувствительности передаточной
функции
(12)
которая определяет первое приближение дополнительной передаточной функции, равной
разности варьируемой и исходной передаточных функций при вариации параметра (13)
Эти зависимости справедливы в том случае, когда вариации параметра не меняют порядка характеристического уравнения системы.
Слайд 16
Функции чувствительности временных характеристик
Может также использоваться так называемая
логарифмическая функция чувствительности:
(14)
строго говоря, может использоваться в тех случаях,
когда и и представляют собой безразмерные величины.
Слайд 17
Функции чувствительности временных характеристик
Найдём дополнительную передаточную функцию для
случая, когда исходная передаточная функция может быть представлена в
виде отношения двух полиномов:(15)
где и вариации полиномов числителя и знаменателя передаточной функции.
Слайд 18
Функции чувствительности временных характеристик
Формула (15) позволяет составить структурную
схему модели чувствительности.
Структурная схема модели чувствительности
Слайд 19
Функции чувствительности временных характеристик
Составим, например, модель чувствительности для
передаточной функции замкнутой системы:
(16)
при вариации параметра .
В
соответствии с изложенным находим . Равенство приращений числителя и знаменателя Ф(s) позволяет упростить схему модели.
Слайд 21
Функции чувствительности временных характеристик
Одной из важнейших характеристик типовой
системы управления, состоящей из управляющего устройства (регулятора) Wp(s) и
объекта W0(s), является относительная функция чувствительности:(17)
где К0 коэффициент усиления объекта. Представим
и, подставив в (17) передаточную функцию замкнутой системы по задающему воздействию
(18)
Слайд 22
Функции чувствительности временных характеристик
(19)
В общем случае, когда передаточная функция зависит от ряда
варьирующих параметров, дополнительная передаточная функция: (20)
Если к системе приложено несколько внешних воздействий [g(t), f1(t),..., fl(t)], то следует найти дополнительные передаточные функции для всех исходных передаточных функций, определённых для каждого внешнего воздействия.
Слайд 23
Функции чувствительности критериев качества
Если в системе произошли изменения
ряда параметров ,
то результирующее изменение некоторой используемой оценки качества:(20)
где варьированное значение оценки качества, а её исходное значение, можно подсчитать по формуле полного дифференциала:
(21)
Слайд 24
Функции чувствительности критериев качества
Так как в большинстве случаев
известны только вероятностные оценки вариации , то целесообразно использование
вероятностных методов. Так, если известны максимальные возможные отклонения , то при их независимости друг от друга можно найти среднеквадратичный максимум отклонения оценки качества:(22)
и среднеквадратичный относительный максимум:
(23)
Слайд 25
Функции чувствительности критериев качества
Если заданы дисперсии отклонения параметров
В качестве критерия оценки качества системы могут использоваться, например, максимум ошибки, коэффициенты ошибок, оценки запаса устойчивости и быстродействия, интегральные оценки и т.п.
Слайд 26
Пример
Пусть передаточная функция разомкнутой системы имеет вид:
Требуется определить
среднеквадратичный максимум отклонения показателя колебательности, если
и , причём изменения параметров независимы.Определим вначале исходное значение показателя колебательности. Для этого необходимо найти максимум модуля частотной передаточной функции (АФХ) замкнутой системы:
Слайд 27
Пример
Исследование на максимум даёт:
при КТ2
Функции
чувствительности, если
Среднеквадратичный максимум отклонения:
Таким образом, в рассматриваемой системе
показатель колебательности
Слайд 28
Контрольные вопросы
Каков физический смысл чувствительности?
Какова математическая интерпретация чувствительности?
Каким
образом получают уравнение чувствительности?
Каким образом получают начальные условия для
решения уравнений чувствительности?Чем обусловлено удобство применения функций чувствительности передаточной функции?
Какую информацию получают по модели чувствительности?
В чём смысл функций чувствительности критериев качества?





























