Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

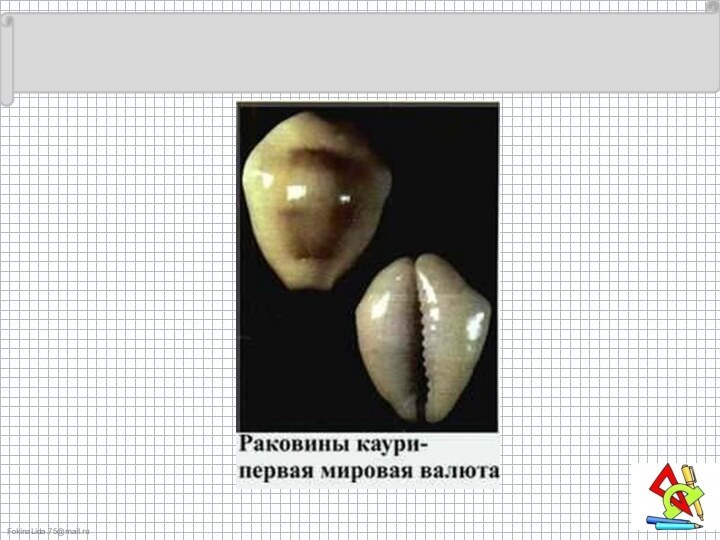
Презентация на тему Из истории денег

Содержание

2. Д Е Н Ь Г И
3. Из истории денег.
7. Кельтские
8. Деревянные деньги.
9. Каменные деньги острова Яп.
10. Кофейные зерна.
11. Мед.
12. Специи.
13. Женьшень.
14. Соль.
15. Перья.
16. Животные.
17. Деньги – это особый товар, служащий единственным
18. Купецкупил самовар за 10 рублей, продал за
19. Решение: расход
24. страна
25. познание окружающего мира спокойная
32. Задача №1. С 1 января 2008 г.
33. Задача №1.
34. Задача №2. Обычная лампа накаливания потребляет электроэнергии
35. Задача №2. Решение:100*7=700(Вт)- за 7ч/сутки
36. Задача №4. Семья из 4-х человек,
37. Задача №4. Решение:894,54 руб. – 100%1418,96 руб.- х%Х=1418,96*100:894,54=158,62454159% -100%= 59% - составит экономия семьи
38. Задача №6. Предприятие разместило в банке
39. Задача №6. Решение:5
40. Задача 9 (о наращенной сумме вклада)Вкладчик
41. Задача 9 (о наращенной сумме вклада) Решение:
42. Экономическая задача 10 : Вкладчик положил
43. Экономическая задача10 Решение:
44. Экономическая задача 11: Вкладчик положил в
45. Экономическая задача 11: Решение:Пусть
46. * Срочный вклад, положенный в сберегательный банк,
47. Ответ *:На
48. Спасибо за внимание!
49. Скачать презентацию
50. Похожие презентации

Д Е Н Ь Г И

Цели:Систематизировать и обобщить полученные знания, продемонстрировать возможность интегрирования математики с экономикой на

Деньги – это особый товар, служащий единственным всеобщим эквивалентом, который выражает стоимость

Купецкупил самовар за 10 рублей, продал за 12 рублей, затем этот же

познание окружающего мира спокойная и безопасная жизнь

Задача №1. С 1 января 2008 г. плата за электроэнергию повысилась с

Задача №2. Обычная лампа накаливания потребляет электроэнергии 100 Ватт/час, а энергосберегающая лампа

Задача №2. Решение:100*7=700(Вт)- за 7ч/сутки потребляет обычная лампа.20*7=140(Вт)- за 7ч/сутки

Задача №4. Семья из 4-х человек, в квартире в которой установлены

Задача №4. Решение:894,54 руб. – 100%1418,96 руб.- х%Х=1418,96*100:894,54=158,62454159% -100%= 59% - составит экономия семьи

Задача №6. Предприятие разместило в банке 5 млн. руб. под 8%

Задача №6. Решение:5 млн. руб. – 100%Х млн.руб.

Задача 9 (о наращенной сумме вклада)Вкладчик положил в банк 10000 руб.

Задача 9 (о наращенной сумме вклада) Решение:

Экономическая задача 10 : Вкладчик положил в банк 3 тыс. рублей,

Экономическая задача 11: Вкладчик положил в банк некоторую сумму денег под

Экономическая задача 11: Решение:Пусть х (руб.) – первоначальный размер

* Срочный вклад, положенный в сберегательный банк, ежегодно увеличивается на 5%.Каким станет

Ответ *:На следующий после вклада год мы

Слайды презентации

Слайд 2 Д Е Н Ь Г И

Слайд 3 Из истории денег.

Слайд 7 Кельтские

Слайд 8 Деревянные деньги.

Слайд 9 Каменные деньги острова Яп.

Слайд 10 Кофейные зерна.

Слайд 12 Специи.

Слайд 13 Женьшень.

Слайд 16 Животные.

Слайд 17 Деньги – это особый товар, служащий единственным всеобщим

Деньги – это особый товар, служащий единственным всеобщим эквивалентом, который выражает

эквивалентом, который выражает стоимость всех товаров и является посредником

в их обмене.

Функции денег:

Мера стоимости

Средства обращения

Средства накопления

Средства платежа

Мировые деньги

Слайд 18 Купец
купил самовар за 10 рублей, продал за 12

Купецкупил самовар за 10 рублей, продал за 12 рублей, затем этот

рублей, затем этот же самовар купил за 13 рублей,

а продал за 14 рублей. Какова была бы прибыль за 30 таких самоваров?
расход доход
? ?

Слайд 19 Решение:
расход

доход
-10-13

+12+14
26-23 = 3(р.)-прибыль с 1 самовара , 3(р.)*30 (шт.) =90 (рублей)

Слайд 24 страна

название банкнот
Латвия

юань
Болгария лев Украина доллар Китай фунт Тенге
Польша Индия лат
США рупия Франция
йена Япония гривна
Великобритания злотый
Казахстан евро

Слайд 25 познание окружающего мира
спокойная и

безопасная жизнь
постоянное саморазвитие
пища

влияние на других людей
модные вещи, одежда любовь
хорошее здоровье уважение близких
хорошо устроенный быт дружба
образование развлечения
общение с природой
общение с людьми

Слайд 32 Задача №1. С 1 января 2008 г. плата

Задача №1. С 1 января 2008 г. плата за электроэнергию повысилась

за электроэнергию повысилась с 1,47р. до 1,66р. На сколько

процентов повысилась плата за электроэнергию? Результат округлите до целых.

Слайд 33 Задача №1. Решение:

1,47р. - 100 %
1,66 – х %

1,47:1,66=100:х
Х=1,66*100:1,47=112,925…
113-100=13%
Ответ: на 13%

Слайд 34 Задача №2. Обычная лампа накаливания потребляет электроэнергии 100

Задача №2. Обычная лампа накаливания потребляет электроэнергии 100 Ватт/час, а энергосберегающая

Ватт/час, а энергосберегающая лампа - 20 Ватт/час. Во сколько

раз энергосберегающая лампа экономичнее обычной лампы накаливания? Сколько рублей в месяц составит экономия, если лампа будет работать 7 часов в сутки? (стоимость электроэнергии в квартире с электрической плитой составляет 1,66 р. за кВт)

Задача №3. Как вы можете помочь сэкономить бюджет семьи?

Слайд 35 Задача №2. Решение:
100*7=700(Вт)- за 7ч/сутки потребляет

обычная лампа.
207=140(Вт)- за 7ч/сутки потребляет энергосберегающая лампа.
70030=21000(Вт)=21(кВт)- в месяц

потребляет обычная лампа.
140*30=42000(Вт)=4,2(кВт)- в месяц потребляет энергосберегающая лампа.
1,66*21=31,86 (руб.) – нужно заплатить за месяц при использовании обычной лампы
1,66*4,2=6,97(руб.) – нужно заплатить за месяц при использовании энергосберегающей лампы.
31,86 - 6,92=24,94 (руб.) – составит экономия

Слайд 36
Задача №4. Семья из 4-х человек, в

квартире в которой установлены приборы учета воды, в месяц

платит за воду 894,54 руб. Сколько процентов составит экономия семьи, если без приборов учета за это же количество воды придется заплатить 1418,96 руб. Результат округлить до целых.

Задача №5.Как семья может сэкономить свой бюджет на водоснабжении?

Слайд 37
Задача №4. Решение:
894,54 руб. – 100%
1418,96

руб.- х%

Х=1418,96*100:894,54=158,62454
159% -100%= 59% - составит экономия семьи

Слайд 38 Задача №6. Предприятие разместило в банке 5

млн. руб. под 8% годовых. Какая сумма будет на

счету предприятия через год?

Задача №7. Банковский вклад в мае увеличился на 10%, а в июне уменьшился на 10%, после чего на счету оказалось 10 890 руб. Найдите сумму вклада на конец апреля.

Задача №8. Как семье сохранить и увеличить свой банковский вклад?

Слайд 39 Задача №6. Решение:
5 млн.

руб. – 100%
Х млн.руб. - 8%
5/х=100/8
Х=5*8:100 =0,4
5+0,4=5,4 млн.руб.-

будет на счету через год
Задача №7. Решение:
Пусть х - сумма вклада на конец апреля.
Вклад в мае - 110%=1,1х руб.
Влад в июне – 0,9*1,1х руб.=0,99х
Зная, что в июне вклад составил 10 890 руб., получим уравнение: 0,99х=10890
Х=10890:0,99=11000 (р.)- сумма вклада на конец апреля.

Задача №8. Как семье сохранить и увеличить свой банковский вклад?

Слайд 40 Задача 9 (о наращенной сумме вклада)
Вкладчик положил

Задача 9 (о наращенной сумме вклада)Вкладчик положил в банк 10000

в банк 10000 руб. Проценты сложные. Какая сумма будет

на счете у вкладчика через три года, если процентная ставка в первый год – 20%, во второй – 30%, в третий – 25%?

Слайд 41 Задача 9 (о наращенной сумме вклада)

Решение:

Слайд 42 Экономическая задача 10 : Вкладчик положил в

Экономическая задача 10 : Вкладчик положил в банк 3 тыс.

банк 3 тыс. рублей, банк выплачивает ему 40 %

годовых. Составьте формулу, задающую зависимость суммы денег, которую вкладчик получит через X лет. Через сколько лет вкладчик получит 5; 10; 15 тыс. рублей?