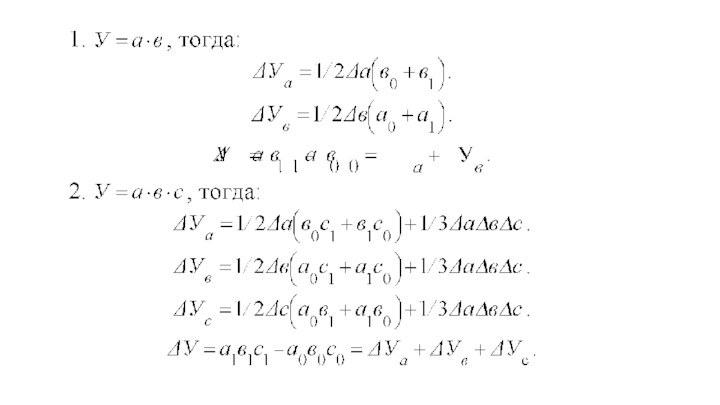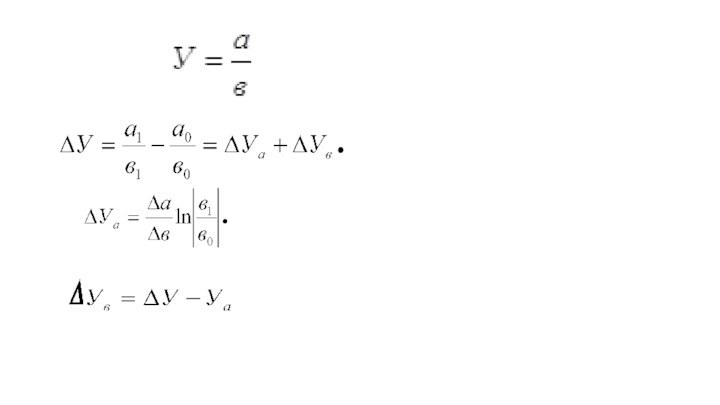Слайд 2
Методы факторного анализа.
Прием цепных подстановок и его разновидности.
Метод
относящийся к группе элиминирования, так же как и индексный
метод.
Но в отличие от индексного используется для всех видов факторных зависимостей (исключение составляют разновидности метода прием абсолютны и относительных разниц) и при любом количестве факторов.
Метод считается универсальным методом изучения. Часто применяется для оценки и прогноза в финансовом анализе, в том числе и программных продуктах и положен в основу всего факторного анализа.
Слайд 3
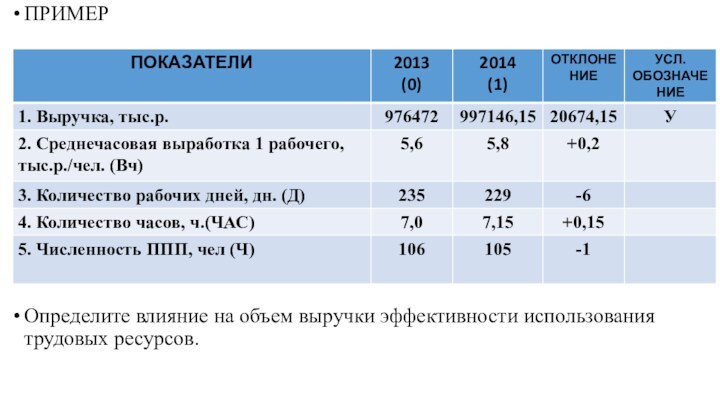
ПРИМЕР
Определите влияние на объем выручки эффективности использования трудовых
ресурсов.
Слайд 4
В данном случае модель факторной зависимости имеет мультипликативный
вид, т.е. выражается формулой У=а*в*с*д . При этом за
У принимается результирующий показатель, в данном случае – выпуск продукции. При определении последовательности расчетов нужно опираться на правила:
В первую очередь учитывают изменение количественных факторов, затем структурных и в последнюю очередь качественных.
Если имеется несколько количественных и качественных факторов, то сначала надо изменить факторы первого порядка воздействия, а затем более низкого уровня подчинения.
После построения модели производятся сначала промежуточные расчеты (правило: количество промежуточных расчетов всегда на 1 больше, чем факторов в модели).
После проведения промежуточных расчетов производится непосредственная оценка влияния факторов на результирующий показатель.
Слайд 5
Разновидности приема абсолютных и относительных разниц
Приемы абсолютных разниц
и относительных разниц, в отличие от метода цепных подстановок,
имеют одно ограничение – они применяются только в случае мультипликативной факторной модели.
Слайд 6
Интегральный метод экономического анализа
Одним из таких способов (методов)
является интегральный. Он находит применение при определении влияния отдельных
факторов с использованием мультипликативных, кратных, и смешанных (кратно-аддитивных) моделей. В условиях применения интегрального метода имеется возможность получения более обоснованных результатов исчисления влияния отдельных факторов, чем при использовании метода цепных подстановок и его вариантов. Метод цепных подстановок и его варианты, а также индексный метод имеют существенные недостатки: 1) результаты расчетов влияния факторов зависят от принятой последовательности замены базисных величин отдельных факторов на фактические; 2) дополнительный прирост обобщающего показателя, вызванный взаимодействием факторов, в виде неразложимого остатка присоединяется к сумме влияния последнего фактора. При использовании же интегрального метода этот прирост делится поровну между всеми факторами.
Слайд 13
Прием взвешенных конечных разностей
Суть метода состоит в том,
что размер влияния каждого фактора определяется по первой, по
второй и по n-й подстановке, потом результат суммируется и от полученной суммы берется средняя величина, характеризующая влияние всех факторов на результативный показатель.
Используя принятые нами обозначения, получим изменение результативного признака за счет первого фактора а:
Изменение результативного признака за счет второго фактора в:
Слайд 14
Баланс факторов:
Недостаток данного метода – он довольно
трудоемкий, так как приходится учитывать все возможные варианты подстановок,
кроме того, при усреднении нельзя получить однозначное количественное значение отдельных факторов.
Слайд 15
Прием простого прибавления неразложимого остатка
Указанный метод описывается в
трудах С.М. Югенбурга, М.И. Баканова, А.Д. Шеремета и состоит
в прибавлении неразложимого остатка к качественному или количественному (основному или второстепенному) фактору или делении данного остатка поровну между двумя факторами.
Получаем следующие рабочие формулы:
Первый вариант:
Δ Уа = Δ а в0 + Δ а Δв = Δа (в0 +Δв) = Δ а в1;
Δ Ув = Δ в а0.
Второй вариант:
Δ Уа= Δ а в 0;
Δ Ув = Δ в а 0+ Δ а Δв = Δв (а0 +Δ а) = Δ в а1.
Третий вариант:
Δ Уа= Δ а в0 +(Δ а Δв) / 2;
Δ Ув = Δ в а 0+ (Δ а Δв) / 2.
Этот метод хотя и нейтрализует проблему неразложимого остатка, но связан с условием определения количественных и качественных факторов, что усложняет задачу при использовании больших факторных систем.
Слайд 16
Метод логарифмирования
Кроме этого метода, в анализе находит применение

также метод (способ) логарифмирования. Он используется при проведении факторного
анализа, когда исследуются мультипликативные модели. Сущность рассматриваемого метода заключается в том, что при его использовании имеет место логарифмически пропорциональное распределение величины совместного действия факторов между ними, то есть эта величина распределяется между факторами пропорционально доле влияния каждого отдельного фактора на сумму обобщающего показателя.
В процессе логарифмирования находят применение не абсолютные величины прироста экономических показателей, как это имеет место при интегральном методе и приеме цепных подстановок, а относительные, то есть индексы изменения этих показателей. К примеру, обобщающий экономический показатель определяется в виде произведения трех факторов — сомножителей f = x y z.
Найдем влияние каждого из этих факторов на обобщающий экономический показатель. Так, влияние первого фактора может быть определено по следующей формуле:
Δfx = Δf • lg(x1 / x0) / lg(f1 / f0)
Слайд 17
Метод логарифмирования
Для нахождения влияния второго фактора воспользуемся следующей
формулой:
Δfy = Δf • lg(y1 / y0) / lg(f1
/ f0)
Влияние третьего фактора, применим формулу:
Δfz = Δf •lg(z1 / z0)/ lg(f1 / f0)
Таким образом, общая сумма изменения обобщающего показателя распределяется между отдельными факторами в соответствии с пропорциями отношений логарифмов отдельных факторных индексов к логарифму обобщающего показателя.
При применении рассматриваемого метода могут быть использованы любые виды логарифмов — как натуральные, так и десятичные.
Слайд 18
Метод дифференциального исчисления
При проведении факторного анализа находит применение
также метод дифференциального исчисления. Последний предполагает, что общее изменение
функции, то есть обобщающего показателя, подразделяется на отдельные слагаемые, значение каждого из которых исчисляется как произведение определенной частной производной на приращение переменной, по которой определена эта производная. Определим влияние отдельных факторов на обобщающий показатель, используя в качестве примера функцию от двух переменных.
Задана функция Z = f(x,y). Если эта функция является дифференцируемой, то ее изменение может быть выражено следующей формулой: