Слайд 2
3. Независимое поведение: объемная конкуренция. Модель Курно
Анализ дуополии
как простейшей формы олигополии впервые был осуществлен в 1838
г. французским экономистом Огюстеном Курно.
Эта модель описывает рыночное равновесие в условия некооперированной олигополии.
Слайд 3
Предпосылки модели Курно
1) Две фирмы производят однородный товар.
2) Фирмам известна кривая рыночного спроса.
3) Фирмы принимают
решения о производстве независимо друг от друга и одновременно.
4) Каждая из фирм предполагает выпуск конкурента постоянным.
Слайд 4
Исходные данные для моделей дуополии
Отраслевой спрос, представлен линейной
функцией:
Р = a – b Q
где a, b
– положительные константы
Q – объем рыночного спроса, складывается из объемов предложения первой (q1) и второй (q2) фирм (Q=q1+q2) при цене P. Тогда линейный спрос можно представить как:
Р = a – b(q1+q2) = a – bq1– bq2
Обе фирмы имеют одинаковые условия по издержкам производства: ТCi = c* qi
где с - положительная константа.
Таким образом, предельные издержки для каждого дуополиста равны средним:
МCi = АCi = c.
Слайд 5
Модель Курно
Прибыли олигополистов можно выразить как:
П1 = TR1
– TC1 = Pq1 – cq1
П2 = TR2 –
TC2 = Pq2 – cq2
Подставив значение P, получим:
П1 = (a – bq1– bq2)q1 – cq1 = a q1 – bq12– bq2q1 – cq1
П2 = (a – bq1– bq2)q2 – cq2 = a q2 – bq2q1 – bq22 –cq2
Слайд 6
Модель Курно
Условие максимизации прибыли предполагает невозможность прироста прибыли
в оптимальной точке, или другими словами равенство производной функции
прибыли по объёму нулю:
Слайд 7
Модель Курно
Перепишем эти уравнения следующим образом:
2bq1 = (a
– c)– bq2
2bq2 = (a – c)– bq1
Выразив
объём выпуска одной фирмы через объём выпуска другой фирмы, мы получим уравнения кривых реакции:
q1 = (a – c)/2b – 0,5q2
q2 = (a – c)/2b – 0,5q1
Слайд 8
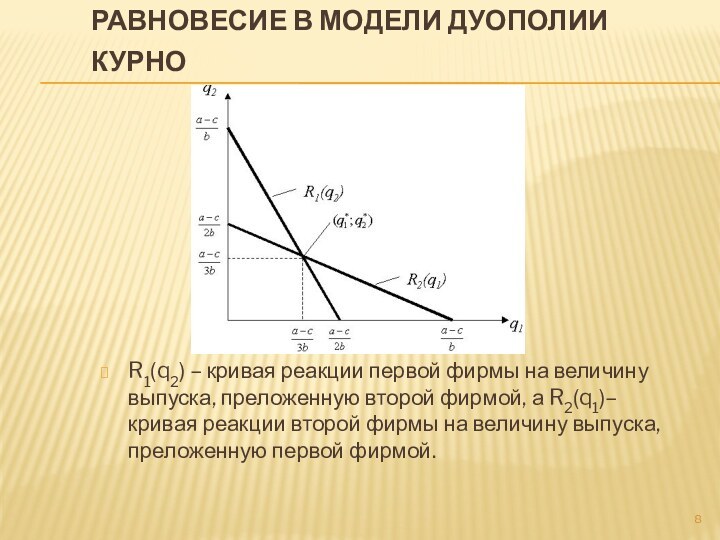
Равновесие в модели дуополии Курно
R1(q2) – кривая
реакции первой фирмы на величину выпуска, преложенную второй фирмой,
а R2(q1)– кривая реакции второй фирмы на величину выпуска, преложенную первой фирмой.
Слайд 9
Равновесие в модели дуополии Курно
Для того чтобы определить
равновесные объёмы выпуска обеих фирм, подставим выражение q2 в
уравнение
q1 = (a – c)/2b – 0,5q2 и наоборот и получим:
q1 *= (a – c)/3b
q2 *= (a – c)/3b.
q1 *= q2 *.
Слайд 10
Равновесие в модели дуополии Курно
Как видно из полученного
уравнения и рисунка, равновесный совокупный объём выпуска обеих фирм
(Q*), которые действуют независимо друг от друга покрывает лишь 2/3 рыночного спроса, равного Q = (a – c)/b:
Слайд 11
Равновесие в модели дуополии Курно
При этом равновесная цена
составит:
Её можно рассчитать, если подставить в функцию спроса выражение
совокупного объёма.
Каждый дуополист, при этом, сможет получить прибыль в размере:
Прибыль можно рассчитать из условия:
Пi = TRi – TCi = Pqi – cqi, подставив соответствующие выражения объёма выпуска каждой фирмы и цены.
Слайд 12
Максимальные значения прибыли
Если конкурент вообще уходит с рынка
то тогда, вся прибыль достается оставшемуся на рынке дуополисту,
который становится монополистом и его равновесный объем выпуска составит:
Объём выпуска мы находим из условия максимизации прибыли, т. е. П '= 0
П = TR – TC = (a – bq)q – cq = aq – bq2– cq,
а П '= a – 2bq– c=0.
Слайд 13
Максимальные значения прибыли
Равновесная цена составит:
А прибыль будет
максимальна в размере:
Слайд 14
Равновесие Курно, договорное равновесие и конкурентное равновесие
К –
равновесие Курно; С – конкурентное
равновесие;
М – договорное равновесие.
R1(q2) – кривая реакции первой фирмы;
R2(q1)– кривая реакции второй фирмы.
Слайд 15
Договорное равновесие
Общеотраслевой объём производства (Qm),будет таким же как
и в случае когда на рынке остаётся одна фирма
(в условиях монополии):
Qm = (a – c)/2b.
Но обеспечивать его будут 2 фирмы. В условиях договорного равновесия объём производства каждой фирмы составит половину от общеотраслевого объёма производства:
q* = (a – c)/4b.
Соответственно равновесная цена составит:
Слайд 16
Конкурентное равновесие
В условиях совершенной конкуренции предельные издержки были
бы равны цене, то есть Р= с, тогда, из
функции спроса :
Р = a – b Q
найдём отраслевой объём производства:
Q = (a – b)/ с.
Тогда объём производства каждой фирмой составит:
q* = (a – c)/2b.
Подобная ситуация может сложиться в результате ценовой войны между олигополистами.
Слайд 17
Сравнение равновесия Курно, договорного равновесия и конкурентного равновесия
Как
видно общеотраслевой объём производства полностью покрывал бы рыночный спрос
только в условиях конкурентного равновесия или ценовой войны.
В ситуации равновесия Курно общеотраслевой объём производства покрывает рыночный спрос на 2/3.
А в случае сговора между фирмами общеотраслевой объём производства покрывает рыночный спрос только на половину.