Слайд 2
Цикл Карно
Изменение внутренней энергии рабочего тела за цикл
равно нулю потому, что тело возвращается в исходное состояние.
Следовательно, вся полученная теплота затрачивается телом на совершение работы:
Коэффициентом полезного действия тепловой машины называется отношение совершаемой за цикл работы A к получаемому от нагревателя за цикл количеству теплоты QAB:
Слайд 3
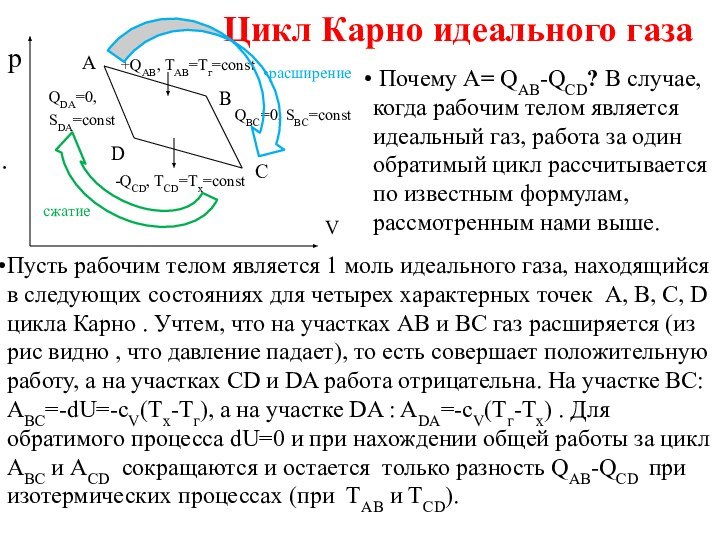
Цикл Карно идеального газа
Почему А=
QAB-QCD? В случае, когда рабочим телом является идеальный газ,
работа за один обратимый цикл рассчитывается по известным формулам, рассмотренным нами выше.
Пусть рабочим телом является 1 моль идеального газа, находящийся в следующих состояниях для четырех характерных точек A, B, C, D цикла Карно . Учтем, что на участках AB и BC газ расширяется (из рис видно , что давление падает), то есть совершает положительную работу, а на участках CD и DA работа отрицательна. На участке ВС: ABC=-dU=-сV(Tх-Тг), а на участке DA : ADA=-сV(Tг-Тх) . Для обратимого процесса dU=0 и при нахождении общей работы за цикл АВС и АСD сокращаются и остается только разность QAB-QCD при изотермических процессах (при ТАВ и ТCD).
A
В
С
D
+QАВ, ТАВ=Tг=const
-QCD, ТCD=Тх=const
QDA=0,
SDA=const
QBC=0, SBC=const
p
V
расширение
сжатие
Слайд 4
Цикл Карно
При Т=const dU=0 и все тепло
идет на
совершение работы :
Точки В и С , так же
как и А и D на одних адиабатах и из уравнения адиабат
Следовательно
Отсюда получим:
Слайд 5
КПД цикла Карно
Подставляя значения QАВ и QCD
в формулу для КПД:
Берем идеальный газ только потому,
что известно его уравнение состояния, и это облегчает вычисление КПД.
Цикл Карно так выбран специально. Те. если бы мы не взяли две изотермы то и => логарифмы не сократились бы и работа за цикл была бы меньше. Изотермы две изотермы соединять не могут => изобары или адиабаты, но изобара идет горизонтально и замкнуть цикл потом не возможно => берем адиабаты.
А если рассматривать в координатах (S,T) то цикл просто занимает всю площадь между прямыми энтропии с S1≠S2=const и больше занять нечего. А площадь равна работе за цикл.
Цикл полностью обратим . Запустим в обратную сторону и получим тепловой насос
Слайд 6
Теоремы Карно
Первая теорема Карно: любая тепловая машина,
работающая при данных температурах нагревателя (Tг) и холодильника (Tх),
не может иметь КПД больше, чем машина, работающая по обратимому циклу Карно при тех же температурах нагревателя и холодильника. Т.е теорема утверждает , что он идеален и лучше уже не придумаешь и можно использовать как меру эффективности других циклов.
Вторая теорема Карно: КПД цикла Карно не зависит от рода рабочего тела, а только от температуры нагревателя и холодильника. Т.е. все подобрано так, что ln сократились все.
Иногда эти две теоремы объединяют в одну теорему Карно с тем же содержанием.
Слайд 7
Особенности цикла Карно
Цикл Карно обладает важной особенностью:
он полностью обратим. Действительно, на всех стадиях он проведен
так, что исключает соприкосновение тел с разными температурами, что исключает возможность необратимых процессов вследствие не нулевой теплопроводности.
Тепловая машина, работающая по циклу Карно, является идеальной тепловой машиной потому, что никакими способами невозможно получить КПД выше значения, полученного нами для КПД цикла Карно. Абсолютный нуль температуры недостижим (это следует из теоремы Нернста), поэтому КПД любой тепловой машины, в том числе и идеальной, всегда меньше единицы.
На практике есть утечки тепла и цикл получается в виде эллипса ( все углы скруглены).
Слайд 8
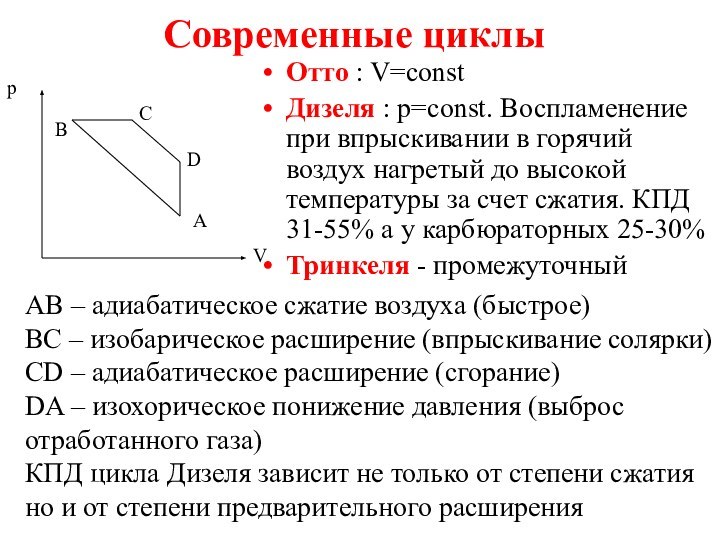
Современные циклы
Отто : V=const
Дизеля : p=const. Воспламенение при
впрыскивании в горячий воздух нагретый до высокой температуры за
счет сжатия. КПД 31-55% а у карбюраторных 25-30%
Тринкеля - промежуточный
A
D
B
C
p
V
АВ – адиабатическое сжатие воздуха (быстрое)
ВС – изобарическое расширение (впрыскивание солярки)
CD – адиабатическое расширение (сгорание)
DA – изохорическое понижение давления (выброс
отработанного газа)
КПД цикла Дизеля зависит не только от степени сжатия
но и от степени предварительного расширения
Слайд 9
Современные разработки в области комнатных температур существуют?
Посмотрим фильм
про магнитный холодильник!
Слайд 10
ТЕПЛОВЫЕ НАСОСЫ
Тепловой насос извлекает накопленную энергию из различных
источников - грунта, рек, озер, морей, стоков, вентиляционных выбросов
и дымовых газов; земных недр и переносит ее в дом. По прогнозу Мирового Энергетического Комитета (МИРЭК), к 2020 году в передовых странах доля отопления и горячего водоснабжения от тепловых насосов составит не менее 75%. Изобрел еще
Кельвин . Он считал, что в силу ограниченности невосстанавливаемых ресурсов у его изобретения большое будущее, а затраты на отопление должны составлять всего 3% от существующих. В его "умножителе тепла", или как сейчас называют, тепловом насосе (Heat Pump), в качестве теплоносителя использовался воздух. Сейчас производятся миллионами!
Слайд 11
Тепловые насосы
Современные тепловые насосы работают полностью
аналогично холодильникам у Вас в квартире. Только если холодильник
откачивает тепло из холодильной камеры наружу (оно рассеивается на задней панели) то тепловой насос перекачивает его с улицы во внутрь дома.
Крайне эффективен так как сам энергию не производит а только перемещает имеющееся тепло (уже запасенное до этого, например, от Солнца) с одного места на другое (с улице в дом).
Хороший потенциал для применения тепловых насосов представляют собой обогреваемый пол. Коэффициент преобразования энергии тем выше, чем меньше разница температур между охлаждаемым и нагреваемым объектом.
Огромный потенциал! За счет тепла воды мирового океана можно снабжать электроэнергией весь мир более тысячи лет понизив температуру менее чем на 0.1 С. Только одна маленькая заминка -второе начало термодинамики!
Слайд 12
Второе начало термодинамики
По 1-му началу термодинамики система
может совершать работу только за счет своей внутренней энергии
или каких либо внешних источников тепла. У второго начала также есть несколько эквивалентных формулировок. Самая простая: невозможен такой периодический процесс, единственным результатом которого является превращение тепла в работу. За период в цикле Карно только часть тепла QAB превращается в работу А, а другая часть QCD передается холодильнику. Периодический двигатель у которого все тепло идет в работу был бы весьма популярен ….но даже для идеального обратимого цикла Карно это не возможно.
Слайд 13
Второе начало термодинамики
2-е начало не противоречит 1-му началу
термодинамики, дополняет его. Вечным двигателем 1-го рода мы назвали
двигатель с КПД более 100% (т.е работа совершается в большем количестве чем полученная извне энергия). Воображаемый двигатель, который всю извлекаемую из окружающей среды (океан, воздух и т.д.) теплоту Q превращает в A назовем вечным двигателем 2-го рода. Вечный двигатель 2-го рода не возможен. Т.е. превратить все подводимое тепло только в полезную работу невозможно. Часть тепла потеряется и перейдет к холодильнику (например, во внешнюю среду). При анализе идеального варианта тепловой машины 2-е начало было учтено. Первым сформулировал Клаузиус в 1850 г.- невозможен процесс при котором теплота переходила самопроизвольно от холодных тел к нагретым тела (в широком смысле единственным следствием которого является переход теплоты от холодильника к нагревателю).
Слайд 14
Демон Максвелла за работой. Иллюстрация пользователя Волобуев

с сайта wikipedia.org
Японские физики собрали искусственного демона Максвелла
Японским физикам
впервые удалось превратить информацию в энергию. Статья ученых опубликована в журнале Nature Physics, а ее краткое изложение приводит Nature News.
В рамках работы ученые поместили бусинку из полистирола продолговатой формы в специальный раствор, который сами организаторы эксперимента называют буферным. Размер бусины составлял около 300 нанометров. Во время эксперимента бусина помещалась в емкость с раствором, на дне которой располагались электроды, на которые подавался переменный ток.
Электромагнитное поле индуцировало на бусинке, выполненной из диэлектрика, поляризацию таким образом, что в поле ей было более энергетически выгодно вращаться по часовой стрелке, чем против нее. Вместе с тем из-за небольших размеров на вращение бусинки оказывало заметное (и случайное) влияние броуновское движение молекул раствора.
Состояние бусинки мониторилось при помощи микроскопа и камеры для высокоскоростной съемки. В зависимости от поведения бусинки фаза одного из электродов менялась. В результате бусинка набирала механическую энергию. Подсчеты исследователей показали, что этой энергии было больше, чем работа, совершаемая электромагнитным полем.
Основой для эксперимента стали теоретические выкладки Лео Сциларда, опубликованные им в работе 1929 года. Ученые подчеркивают, что закон сохранения энергии в данном случае не нарушается, поскольку для работы ЭВМ и камер требуется электрическая энергия. Вместе с тем непосредственно передачи энергии бусинке, потраченной на работу того же ЭВМ, не происходит - в рамках эксперимента происходит превращение информации в энергию и наоборот.
Физики отмечают, что на создание данного эксперимента их вдохновил знаменитый демон Максвелла. В 1867 году Джеймс Максвелл предложил мысленный эксперимент, якобы опровергающий второе начало термодинамики. В рамках эксперимента имелось две емкости с газом, разделенные дверью и демон, который был способен открывать и закрывать эту самую дверь.
Предполагалось, что демону известны скорости молекул - перед быстрыми он открывал дверь, а перед медленными, наоборот, закрывал. В результате одна из емкостей нагревалась, а вторая остывала. В это же время Второе начало термодинамики утверждает, что самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому, невозможен.
Ссылки по теме
Слайд 15
Вернемся снова к энтропии
Энтропией называется функция состояния
системы, изменение которой S для равновесного (обратимого) перехода системы
из состояния 1 в состояние 2 равно:
δQ>δQнеоб и знак “=” в формуле меняем на “>”
У функцией состояния при обратимом круговом процессе значение интеграла не зависит от пути, по которому идет процесс (например, в цикле Карно), а при необратимом <0 . Это неравенство Клаузиуса и следствие теоремы Карно. В общем случае Q/TdS. Те. в результате цикла энтропия либо возрастает либо остается постоянной. При обратимом переходе из состояния 1 в 2 S будет одним и тем же. Оно определяется только S1 и S2
Слайд 16
Энтропия
S не может быть измерена непосредственно можно только
пересчитать S.
Выражение для энтропии позволяет определить не абсолютное
значение функции S, соответствующее какому-то состоянию, а лишь ее изменение при переходе от одного состояния к другому. Поэтому можно приписать некоторому состоянию системы значение S = 0 и сравнивать с ним все другие состояния системы.
S пропорциональна массе вещества . Т.е. величина экстенсивная и часто измеряется на м3, кг и т.д.
S аддитивная величина т.е. Sсис =∑ Si
S (T,V) функция Т и V но определена с точностью до const определяемой теоремой Нернста т.е при Т->0 S ->0
Слайд 17
Второе начало и энтропия
Частные производные –уравнения состояния
Изолированными (или
замкнутыми) системами называются термодинамические системы, которые не обмениваются с
внешней средой ни энергией, ни веществом
Еще одна формулировка: Энтропия изолированной системы не может убывать: dS ≥ 0
То , что dS=0 при δQ=0 => из определения S
Процесс S=const - изоэнтропийный процесс например адиабатическое размагничивание. Т.е. если S1=S2 то система адиабатически изолирована
Энтропия это мера необратимости
Слайд 18
Второе начало и энтропия
При адиабатических условиях возможны только
обратимые процессы (S=const) и не обратимые при которых
S возрастает но в природе все необратимо
Для открытых систем S может и уменьшаться.
Не обязательно чтобы увеличивалась S каждого из тел участвующих в процессе. Увеличивается ∑Si в которых процесс вызвал изменения
S=Sm+Sl+Se=const то -ΔSm=ΔSl+ΔSe
Термодинамическое равновесие – состояние с Smax . Если S= Smax то никакие дальнейшие процессы не возможны ибо любой процесс ведет к уменьшению S.
S(T) может иметь и несколько Smax несколько состояний равновесия (метастабильных состояний). Наиболее стабильно то где самая большая Smax .Т.е. самое большое время жизни состояния . А может вообще не быть стабильных состояний.
Слайд 19
Энтропия обратимых и необратимых процессов
Итак можно показать,
что для любого обратимого процесса энтропия замкнутой системы не
изменяется:
dS=0
При необратимых же процессах: dS>0
Пример необратимого процесса: смешаем массы воды или два газа с разными температурами T1 и T2. Процесс смешения и установления единой температуры может идти сам собой, но обратный процесс разделения смешанных масс ни в коем случае идти не может. При этом необратимом процессе энтропия непрерывно возрастает, но только до установления равновесия.
Слайд 20
Термодинамическая вероятность состояния
Во всякой системе, предоставленной самой
себе, процесс пойдет так, что система будет переходить от
менее вероятных состояний к более вероятным. Состояние равновесия - это всегда наиболее вероятное состояние и энтропия при этом максимальна. Отсюда следует, что энтропия и термодинамическая вероятность состояния — связанные между собой понятия.
Термодинамическая вероятность принципиально отличается от той вероятности, которая обычно нами используется. Например, вероятность выигрыша в лотерею - x%, вероятность падения монеты орлом вверх - 50%, то есть вероятность этих событий всегда меньше или равна единице.
Термодинамическая вероятность состояния (или статистическим весом) называется число способов, которым это состояние осуществляется. Термодинамическая вероятность всегда больше единицы.
Слайд 21
Энтропия и термодинамическая вероятность состояния
Больцман показал, что величина
энтропии и вероятностью состояния связаны следующим образом:
S=-k ln
w
где k — постоянная Больцмана, a w-термодинамическая вероятность состояния системы (число микросостояний, реализующих данное микросостояние
Итак рост энтропии соответствует переходу системы к большему беспорядку. В состоянии равновесия беспорядок максимальный. С физической точки зрения энтропия является мерой беспорядка системы.
Слайд 22
О тепловой смерти Вселенной.
2-е начало термодинамики
получено из обобщения опытных данных для замкнутой и конечной
системы. А если об этом забыть? Если, например, применить 2-е начало к Вселенной, то получаем, что "энтропия Вселенной стремится к максимуму". Значит, когда этот максимум будет достигнут, во Вселенной прекратятся какие бы то ни было тепловые процессы, потому что все тела принимают одинаковую температуру, и все виды энергии переходят в тепловую.
Слайд 23
О тепловой смерти Вселенной.
Действительно, если найдется хоть одно
тело с другой температурой, то будет реализовываться процесс теплопередачи,
который обязательно, по второму началу, приведет к росту энтропии системы, а это невозможно, потому что энтропия уже достигла максимума. Такое состояние системы и названо тепловой смертью Вселенной. На самом деле никакой тепловой смерти нет, т.к. нет никаких оснований считать Вселенную ни конечной, ни замкнутой системой.
2-е начало термодинамики не применимо ко всей Вселенной так как это открытая система!
Слайд 24
Энтропия биосферы
Открытые (незамкнутые) системы физикой также изучаются, но
в рамках термодинамики необратимых процессов (в рамках неравновесной термодинамики).
Биосфера
является открытой системой, и за счет потока солнечной энергии энтропия биосферы может понижаться. И такое понижение энтропии биосферы действительно происходило на протяжении многих миллионов лет. При этом происходило непрерывное повышение организованности биосферы.
Можно сказать, что для биосферы Солнце является источником потока "отрицательной энтропии".
Слайд 25
Энтропия биосферы
Огромные запасы "отрицательной энтропии" накапливались в биосфере
за счет деятельности фотосинтеза, и они хранятся в ископаемом
органическом топливе. Это топливо является примером системы, находящейся в состоянии неустойчивого равновесия, т.е. в нем рост энтропии практически не происходит.
Человек выступает как активный катализатор механизма роста энтропии, сжигая это топливо. Копились запасы отрицательной энтропии миллионы лет, а сжигаются стремительно. В результате энтропия биосферы стала возрастать, что мы и наблюдаем в виде глобального потепления.
Слайд 26
ФАКУЛЬТАТИВНО: Летать или плавать?
Самолет тратит 10 кубических сантиметров
в секунду или 36 литров в час, за который
пролетает 900 километров (необходимо 4 литра на каждые сто километров на 1 пассажира). Современные самолеты чуть более экономные и тратят около 3 литров на сотню километров на одного пассажира.
Ну а что насчет корабля? Большая пассажирская лодка или круизный лайнер потребляют около 25 литров на сто километров на одного пассажира. Несмотря на умеренную скорость, корабль оказывается хуже самолета, если говорить о потреблении топлива на один «пассажирокилометр».