Слайд 2
Подобно понятию гравитационной массы тела в механике Ньютона,
понятие заряда в электродинамике является первичным, основным понятием.
Электрический заряд
– это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Электрический заряд обычно обозначается буквами q или Q.
Слайд 3
Совокупность всех известных экспериментальных фактов позволяет сделать следующие
выводы:
Существует два рода электрических зарядов, условно названных положительными и
отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Слайд 4
Одним из фундаментальных законов природы является экспериментально установленный
закон сохранения электрического заряда.
В изолированной системе алгебраическая сумма зарядов
всех тел остается постоянной:
ԛ1 + ԛ2 + ԛ3 + …+ ԛn = const
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.
Слайд 5
Закон Кулона
Точечным зарядом называют заряженное тело, размерами которого в
условиях данной задачи можно пренебречь.
Сила взаимодействия двух точечных зарядов
в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.
Слайд 7
На основании многочисленных опытов Кулон установил следующий закон:
Силы
взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и
обратно пропорциональны квадрату расстояния между ними:
Слайд 9
Закон Кулона справедлив для точечных заряженных тел. Практически
закон Кулона хорошо выполняется, если размеры заряженных тел много
меньше расстояния между ними.
Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).
Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.
Слайд 11
ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ — величина e, показывающая, во сколько раз
сила взаимодействия двух электрических зарядов в среде меньше, чем
в вакууме.
Слайд 12
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции.
Если заряженное тело взаимодействует одновременно с несколькими заряженными телами,
то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.
Слайд 13
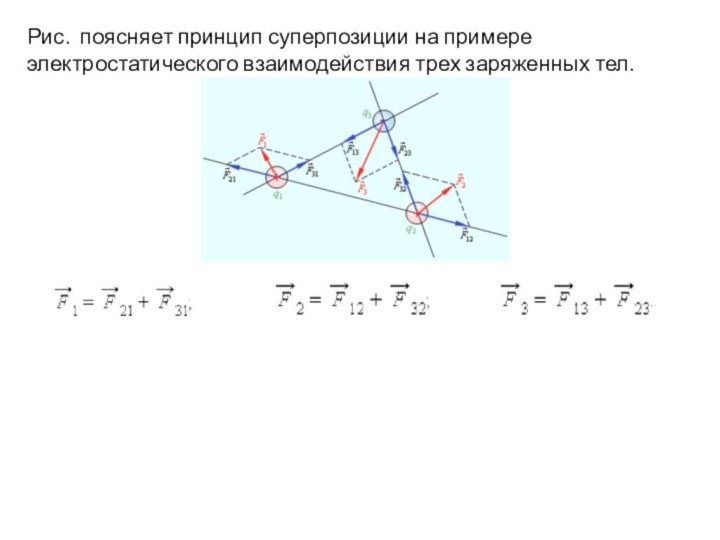
Рис. поясняет принцип суперпозиции на примере электростатического взаимодействия
трех заряженных тел.
Слайд 14
Историческая справка(о пользе публикаций).
Закон Кулона был открыт Кавендишем в 1771
году. В 1785 году Кулон вновь открыл закон своего имени, и
лишь в 1879 году Максвелл - первый директор Кавендишской лаборатории нашел в архивах и опубликовал рукопись Кавендиша. «Что касается скрытности Кавендиша, то она совершенно непростительна. Это грех». ( Хевисайд). Этот «грех» стоил Кавендишу славы первооткрывателя.
Слайд 21
Какой график соответствует зависимости модуля сил взаимодействия F двух точечных
зарядов от модуля одного из зарядов q при неизменном расстоянии между
ними?
1) 1
2) 2
3) 3
4) 4
Слайд 29
Электрическое поле, окружающее заряженное тело, можно исследовать с
помощью так называемого пробного заряда – небольшого по величине точечного заряда,
который не производит заметного перераспределения исследуемых зарядов.
Для количественного определения электрического поля вводится силовая характеристика напряженность электрического поля.
Слайд 30
Напряженностью электрического поля называют физическую величину, равную отношению
силы, с которой поле действует на положительный пробный заряд,
помещенный в данную точку пространства, к величине этого заряда:
Слайд 31
Напряженность электрического поля – векторная физическая величина. Направление
вектора в каждой точке пространства совпадает с направлением силы,
действующей на положительный пробный заряд.
Слайд 32
Электрическое поле неподвижных и не меняющихся со временем
зарядов называется электростатическим. Во многих случаях для краткости это
поле обозначают общим термином – электрическое поле
Слайд 34
Напряженность не зависит от величины заряда, помещенного в
поле.
Вектор напряженности направлен от положительного заряда и к
отрицательному.
Слайд 36
Если с помощью пробного заряда исследуется электрическое поле,
создаваемое несколькими заряженными телами, то результирующая сила оказывается равной
геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:
Слайд 37
Это свойство электрического поля означает, что поле подчиняется принципу
суперпозиции.
В соответствии с законом Кулона напряженность электростатического поля, создаваемого
точечным зарядом Q на расстоянии r от него, равна по модулю
Слайд 38
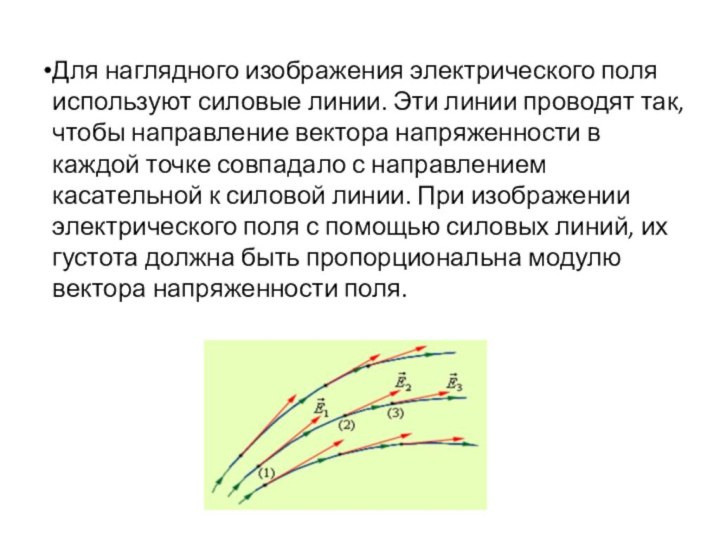
Для наглядного изображения электрического поля используют силовые линии.
Эти линии проводят так, чтобы направление вектора напряженности в
каждой точке совпадало с направлением касательной к силовой линии. При изображении электрического поля с помощью силовых линий, их густота должна быть пропорциональна модулю вектора напряженности поля.
Слайд 39
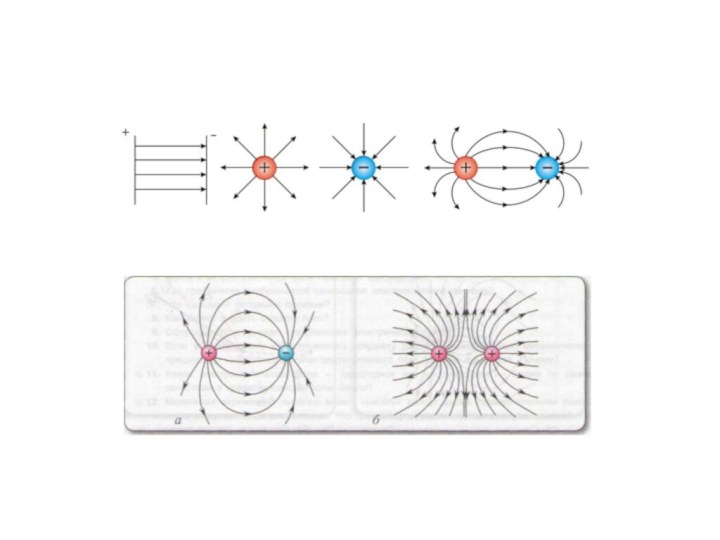
Свойства:
1. Начинаются на положительных и заканчиваются на отрицательных зарядах.
2. Не
пересекаются.
3. Густота линий тем больше, чем больше напряженность. Т.е. напряженность
поля прямо пропорциональна количеству силовых линий, проходящих через единицу площади поверхности.
Слайд 42
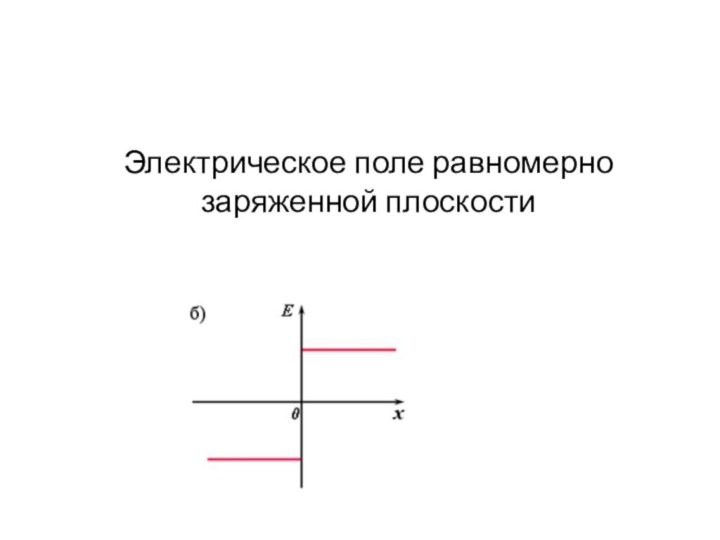
Электрическое поле равномерно заряженной плоскости
Слайд 44
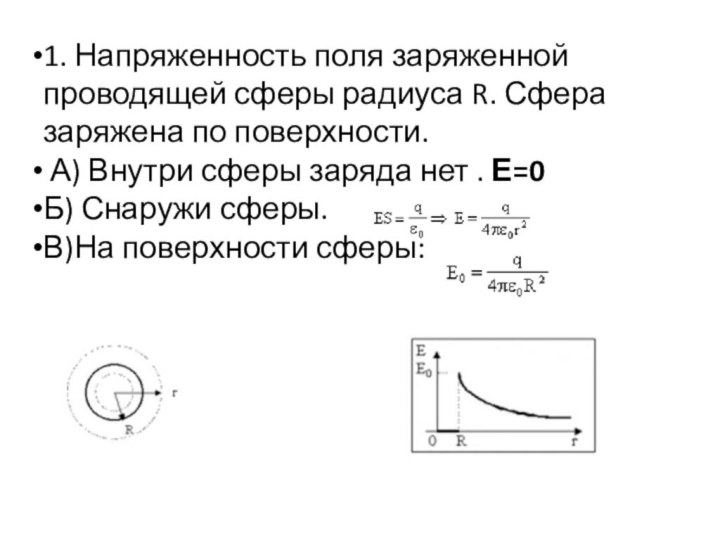
1. Напряженность поля заряженной проводящей сферы радиуса R. Сфера
заряжена по поверхности.
А) Внутри сферы заряда нет . Е=0
Б) Снаружи сферы.
В)На
поверхности сферы:
Слайд 45
Напряженность электрического поля измеряют с помощью пробного заряда .
Если величину пробного заряда уменьшить в n раз, то модуль напряженности
измеряемого поля
1) не изменится
2) увеличится в n раз
3) уменьшится в n раз
4) увеличится в n2 раз
Слайд 46
Напряженность электрического поля измеряют с помощью пробного заряда .
Если величину пробного заряда уменьшить в n раз, то модуль напряженности
измеряемого поля
1) не изменится
2) увеличится в n раз
3) уменьшится в n раз
4) увеличится в n2 раз
Решение. Сила, с которой электрическое поле действует на пробный электрический заряд пропорциональна величине этого заряда, поэтому величина напряженности эле
ктрического поля не зависит от величины пробного заряда .
Слайд 47
Как изменится ускорение заряженной пылинки, движущейся в электрическом
поле, если её заряд увеличить в 2 раза, а
напряжённость поля уменьшить в 2 раза? Силу тяжести не учитывать.
1) увеличится в 2 раза
2) не изменится
3) увеличится в 4 раза
4) уменьшится в 2 раза
Слайд 49
Как изменится ускорение заряженной пылинки, движущейся в электрическом
поле, если и заряд пылинки, и напряжённость поля увеличить
в 2 раза? Силу тяжести не учитывать.
1) увеличится в 2 раза
2) уменьшится в 4 раза
3) не изменится
4) увеличится в 4 раза
Слайд 54
На рисунке показано расположение двух неподвижных точечных электрических
зарядов и . В какой из трех точек — А, B или C — модуль вектора напряженности
суммарного электрического поля этих зарядов максимален?
1) в точке А
2) в точке B
3) в точке C
4) во всех трех точках модуль напряженности поля имеет одинаковые значения
Решение. Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом, — от заряда. Следовательно, в точках A и C поля направлены в разные стороны, а в точке B сонаправлены. Поле точечного заряда по модулю пропорционально величине заряда и обратно пропорционально квадрату расстояния до него: . Таким образом, модуль вектора напряженности суммарного электрического поля этих зарядов максимален в точке B.
Правильный ответ: 2.
Слайд 71
Потенциал. Разность потенциалов. Напряжение. Эквипотенциальные поверхности
Слайд 72
Потенциал электрического поля это энергетическая характеристика поля.
Он представляет собой работу которую нужно совершить против сил
электрического поля для того чтобы переместить единичный положительный точечный заряд находящийся на бесконечности в данную точку поля. Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду
Потенциал не зависит от величины заряда, помещенного в это поле.
Слайд 73
Т.к. потенциальная энергия зависит от выбора системы координат,
то и потенциал определяется с точностью до постоянной.
За точку отсчета потенциала
выбирают в зависимости от задачи:
а) потенциал Земли,
б) потенциал бесконечно удаленной точки поля,
в) потенциал отрицательной пластины конденсатора.
Слайд 74
- следствие принципа суперпозиции полей (потенциалы складываются алгебраически).
Слайд 75
Потенциал численно равен работе поля по перемещению единичного положительного заряда
из данной точки электрического поля в бесконечность.
В СИ
потенциал измеряется в вольтах:
Слайд 76
Разность потенциалов
Работа в электрическом поле
Слайд 77
Напряжение — разность значений потенциала в начальной и конечной точках траектории.
Напряжение численно
равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых
линий этого поля.
Разность потенциалов (напряжение) не зависит от выбора
системы координат!
Слайд 78
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении
положительного заряда в 1 Кл вдоль силовых линий поле
совершает работу в 1 Дж.
Слайд 79
Связь между напряженностью и напряжением.
Слайд 80
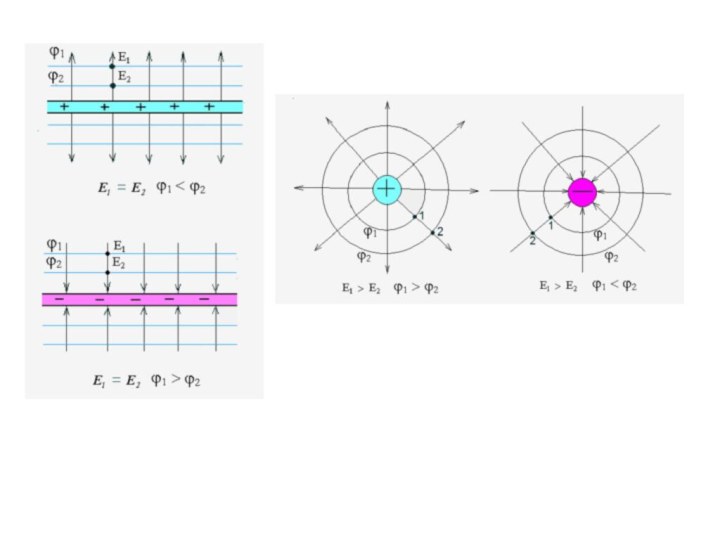
Электрическое поле существует, если существует разность потенциалов.
Единица напряженности:
- Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися
на расстоянии 1 м друг от друга существует разность потенциалов 1 В.
Из этого соотношения видно:
Вектор напряженности направлен в сторону уменьшения потенциала.
Слайд 96
Потенциал заряженного шара
а) Внутри шара Е=0, следовательно, потенциалы во всех
точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на
поверхности шара.
б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда.
Слайд 104
Эквипотенциальные поверхности.
ЭПП - поверхности равного потенциала.
Свойства ЭПП:
- работа
при перемещении заряда вдоль эквипотенциальной поверхности не совершается;
- вектор
напряженности перпендикулярен к ЭПП в каждой ее точке.
Слайд 114
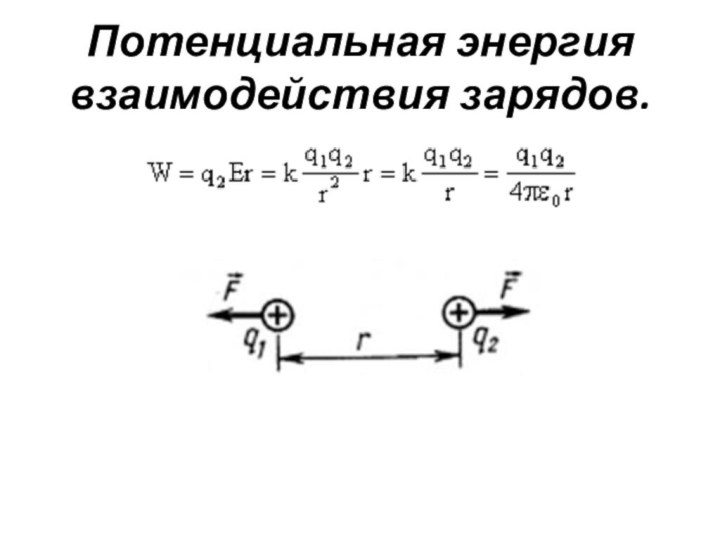
Потенциальная энергия взаимодействия зарядов.
Слайд 118
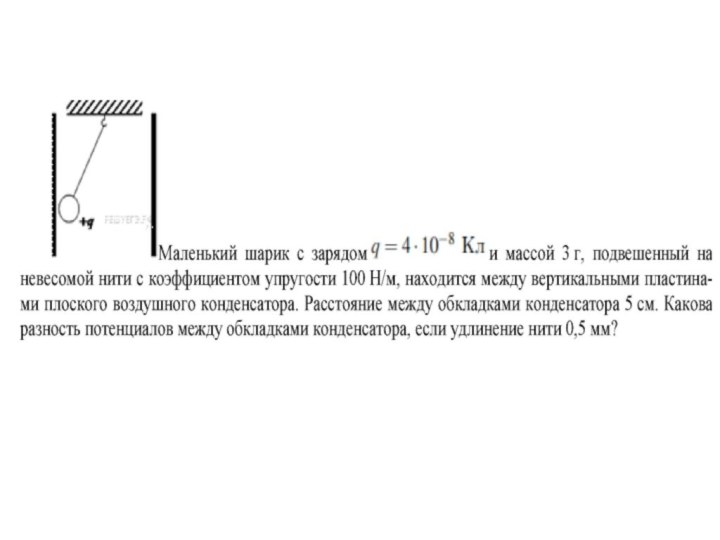
Маленький шарик с зарядом и массой 3 г, подвешенный
на невесомой нити с коэффициентом упругости 100 Н/м, находится между
вертикальными пластинами плоского воздушного конденсатора. Расстояние между обкладками конденсатора 5 см. Какова разность потенциалов между обкладками конденсатора, если удлинение нити 0,5 мм?
Слайд 121
Электроемкость. Конденсаторы
Если двум изолированным друг от друга проводникам
сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов Δφ, зависящая
от величин зарядов и геометрии проводников. Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U. Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q1 = – q2 = q. В этом случае можно ввести понятие электрической емкости.
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
Слайд 122
В системе СИ единица электроемкости называется фарад (Ф):
Поле плоского конденсатора
Идеализированное
представление поля плоского конденсатора. Такое поле не обладает свойством
потенциальности
Слайд 123
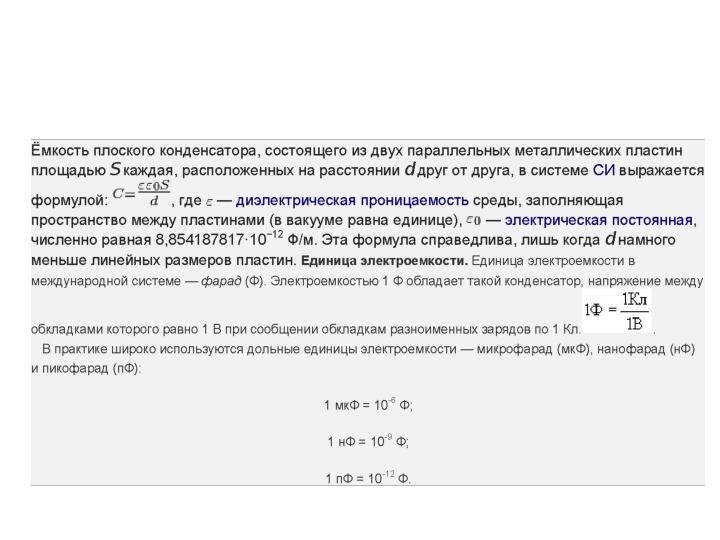
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади
пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если
пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
Слайд 124
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов.
Слайд 126
Последовательное соединениеконденсаторов
Слайд 130
Формулу, выражающую энергию заряженного конденсатора, можно переписать в
форме
Слайд 131
Плоский воздушный конденсатор имеет емкость C. Как изменится его
емкость, если расстояние между его пластинами уменьшить в 3
раза?
1) увеличится в 3 раза
2) уменьшится в 3 раза
3) увеличится в 9 раз
4) уменьшится в 9 раз
Слайд 133
Как изменится емкость плоского воздушного конденсатора, если площадь
обкладок уменьшить в 2 раза, а расстояние между ними
увеличить в 2 раза?
1) увеличится в 2 раза
2) уменьшится в 2 раза
3) не изменится
4) уменьшится в 4 раза
Слайд 135
Как надо изменить заряд на обкладках плоского конденсатора,
чтобы после увеличения зазора между обкладками в 3 раза,
напряженность электрического поля в зазоре уменьшилась в итоге вдвое?
1) увеличить в 4 раза
2) оставить прежним
3) уменьшить в 2 раза
4) увеличить в 2 раз
Слайд 139
В подключенном к источнику постоянного тока плоском конденсаторе
при увеличении в 2 раза расстояния между обкладками энергия
электрического поля
1) увеличится в 2 раза
2) увеличится в 4 раза
3) уменьшится в 2 раза
4) уменьшится в 4 раза
Слайд 141
Плоский воздушный конденсатор изготовлен из двух одинаковых квадратных
пластин со стороной а, зазор между которыми равен d. Другой плоский
конденсатор изготовлен из двух одинаковых квадратных пластин со стороной а/3, зазор между которыми также равен d, и заполнен непроводящим веществом. Чему равна диэлектрическая проницаемость этого вещества, если электрические ёмкости данных конденсаторов одинаковы?
1) 3
2) 6
3) 8
4) 9
Слайд 145
Закон Джоуля - Ленца.
Количество теплоты, выделившееся при прохождении
электрического тока по проводнику, прямо пропорционально квадрату силы тока,
сопротивлению проводника и времени, в течение которого шел ток
Слайд 146
Работа и мощность электрического тока.
Мощность электрического тока (работа
в единицу времени): Работа электрического тока:
Слайд 161
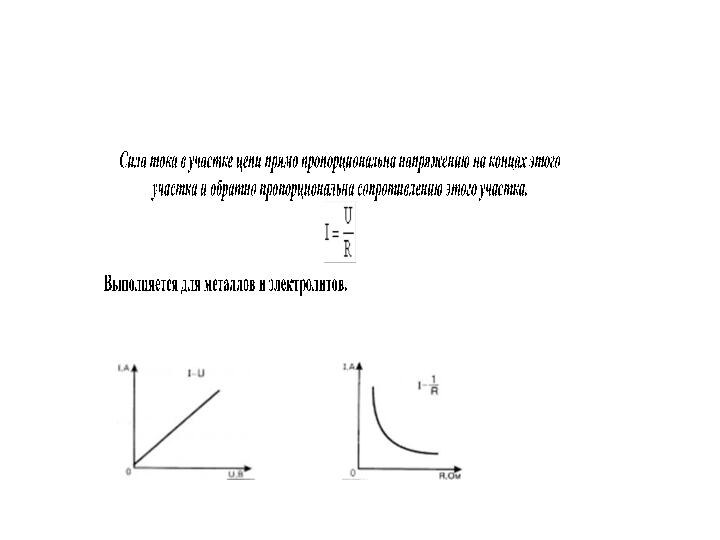
На графике изображена зависимость силы тока в проводнике
от напряжения между его концами. Чему равно сопротивление проводника?
1)
5 0м
2) 4 Ом
3) 0,25 Ом
4) 20 Ом
Слайд 164
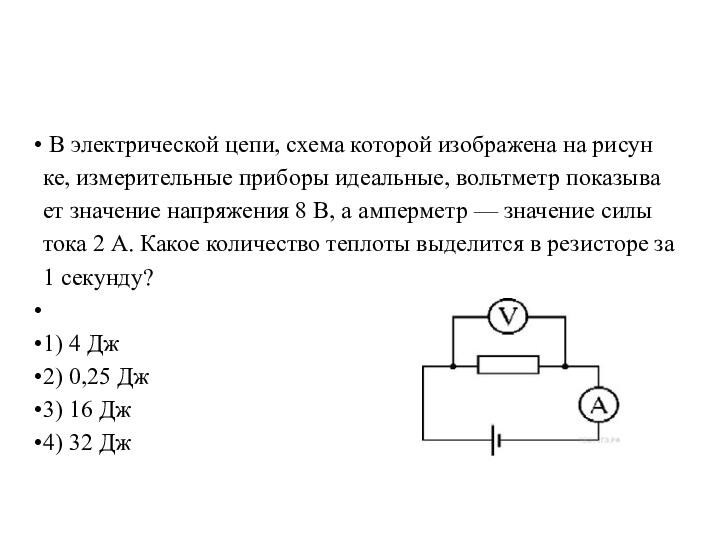
В электрической цепи, схема которой изображена на рисунке,
измерительные приборы идеальные, вольтметр показывает значение напряжения 8 В,
а амперметр — значение силы тока 2 А. Какое количество теплоты выделится в резисторе за 1 секунду?
1) 4 Дж
2) 0,25 Дж
3) 16 Дж
4) 32 Дж
Слайд 166
Задание 15 № 4088. На рисунке изображена схема электрической цепи, включающей
источник постоянного тока, идеальный вольтметр, ключ и резистор. Показание
вольтметра при замкнутом ключе в 3 раза меньше, чем показание вольтметра при разомкнутом ключе.
Можно утверждать, что внутреннее сопротивление источника тока
1) в 3 раза больше сопротивления резистора
2) в 3 раза меньше сопротивления резистора
3) в 2 раза больше сопротивления резистора
4) в 2 раза меньше сопротивления резистора
Слайд 217
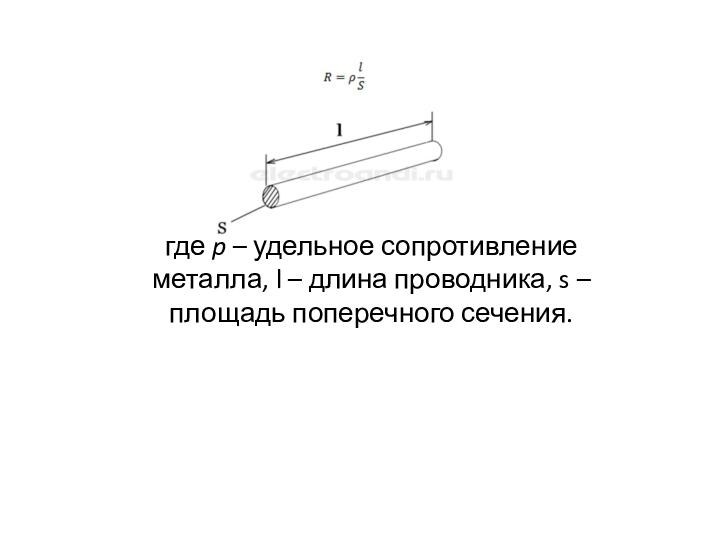
Уде́льное электри́ческое сопротивле́ние, или просто удельное сопротивление вещества
— физическая величина, характеризующая способность вещества препятствовать прохождению электрического
тока.
Слайд 221
где p – удельное сопротивление металла, l – длина проводника,
s – площадь поперечного сечения.