- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Движение материальной точки по окружности
Содержание
- 2. Равномерное движение точки по окружности.
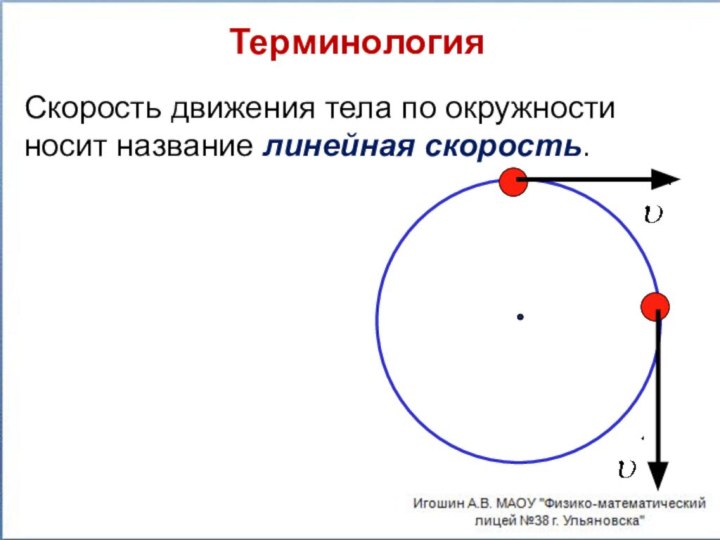
- 3. Терминология Скорость движения тела по окружности носит название линейная скорость.
- 4. Линейная скорость направлена по касательной к траектории и совпадает с направлением движения.
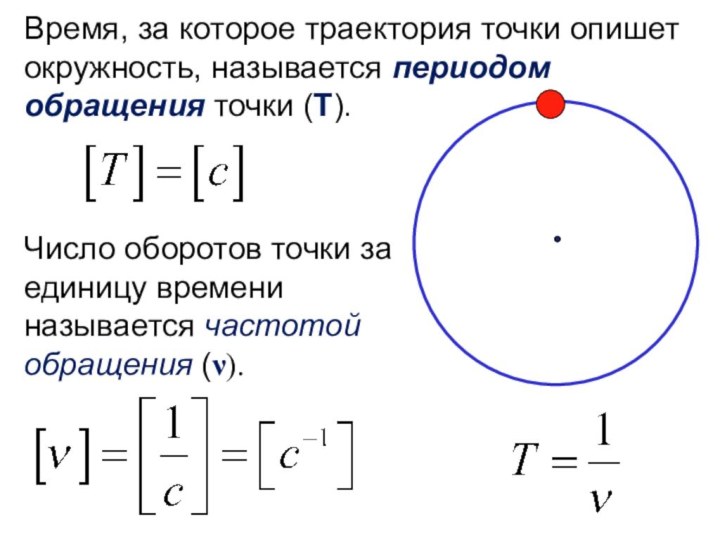
- 5. Время, за которое траектория точки опишет окружность,
- 6. 12RrРавномерное движение по окружности – это простейший пример криволинейного
- 7. Центростремительное (нормальное) ускорение.
- 8. АА1ОСВЗа Δt:Центростремительное (нормальное) ускорение — ускорение точки, характеризующее быстроту изменения направления вектора скорости.
- 9. За один полный оборот S=2πR, t=Т.Скорость при равномерном прямолинейном движении
- 10. АА1ОСВВектор мгновенного ускорения направлен по радиусу к центру окружностиЦентростремительное (нормальное) ускорениеА1
- 11. Тангенциальное (касательное), центростремительное (нормальное) и полное ускорения.
- 12. Если тело движется по окружности неравномерно, то
- 13. АВускоренноезамедленное
- 14. Угловая скорость и угловое ускорение.
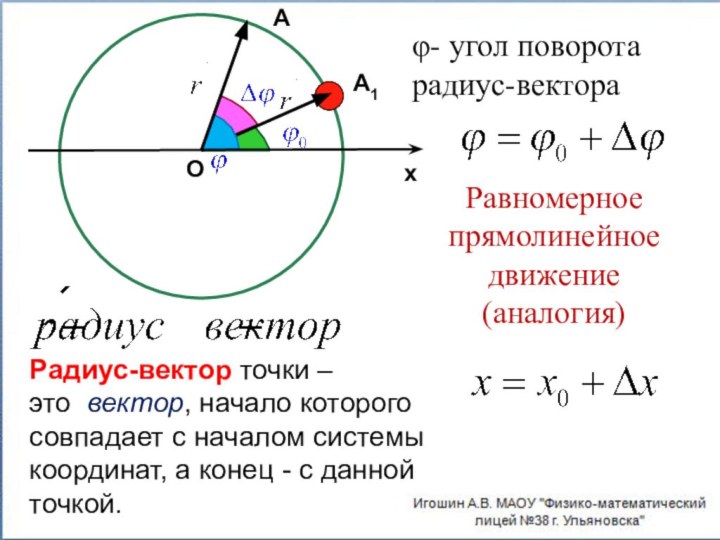
- 15. АА1ОxРадиус-вектор точки – это вектор, начало которого совпадает
- 16. Угловой скоростью при равномерном движении по окружности
- 17. Равномерное прямолинейное движение (аналогия)
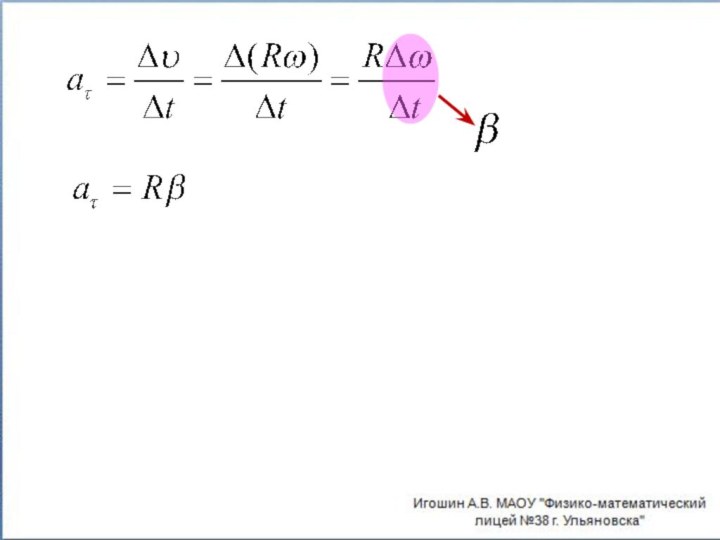
- 18. Угловое ускорение величина, характеризующая быстроту изменения угловой
- 19. Скорость при равнопеременном движении по окружностиускоренноезамедленноеРавнопеременное прямолинейное движение (аналогия)
- 20. Уравнение равнопеременного движения точки по окружностиускоренноезамедленноеРавнопеременное прямолинейное движение (аналогия)
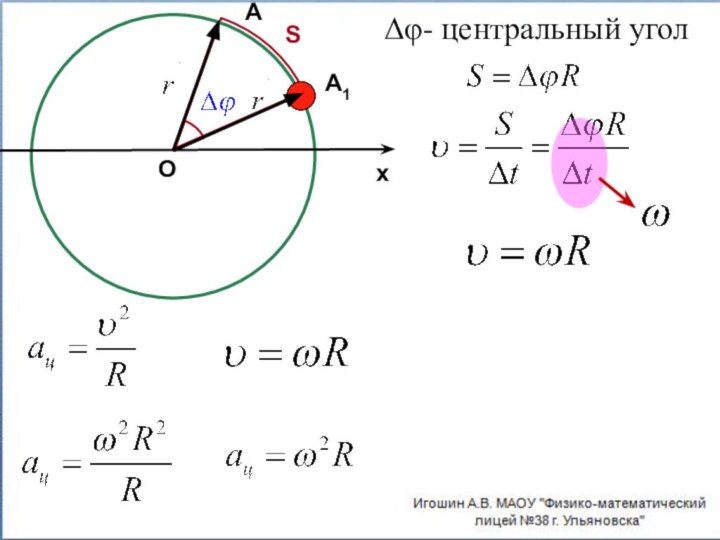
- 21. Связь между линейными и угловыми величинами.
- 22. АА1ОxΔφ- центральный уголS
- 23. Скачать презентацию
- 24. Похожие презентации
Равномерное движение точки по окружности.
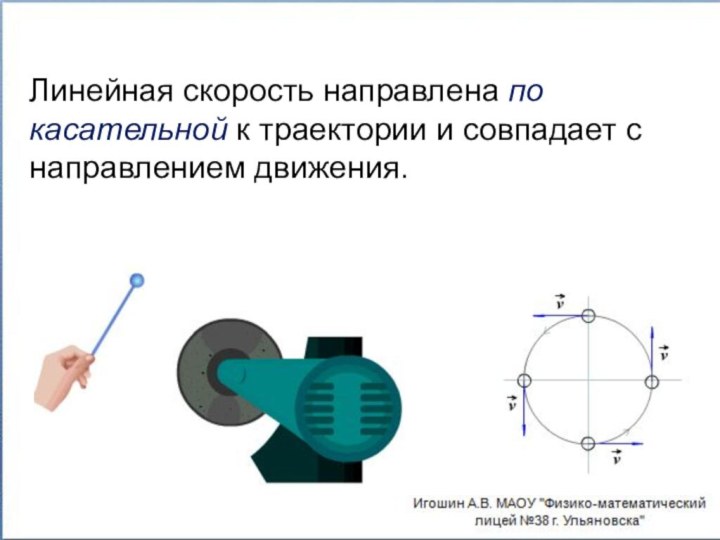
Слайд 4 Линейная скорость направлена по касательной к траектории и
совпадает с направлением движения.
Слайд 5 Время, за которое траектория точки опишет окружность, называется
периодом обращения точки (Т).
Число оборотов точки за единицу времени
называется частотой обращения (ν).
Слайд 6
1
2
R
r
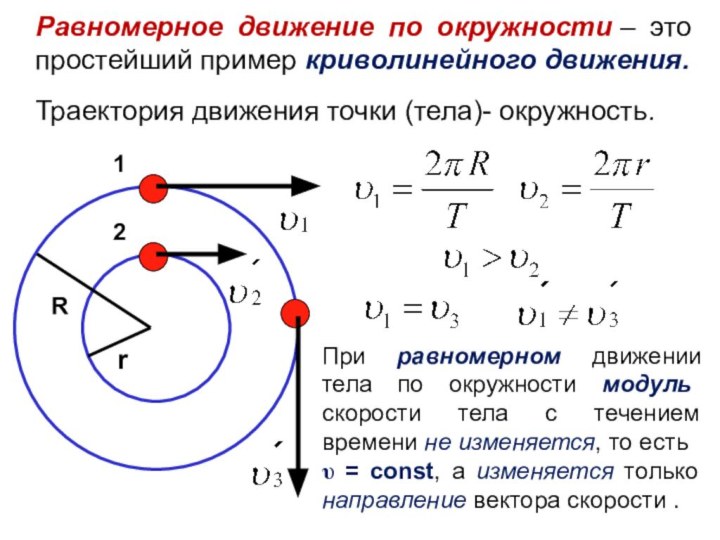
Равномерное движение по окружности – это простейший пример криволинейного движения.
Траектория
движения точки (тела)- окружность.
При равномерном движении тела по окружности
модуль скорости тела с течением времени не изменяется, то есть υ = const, а изменяется только направление вектора скорости .
Слайд 8
А
А1
О
С
В
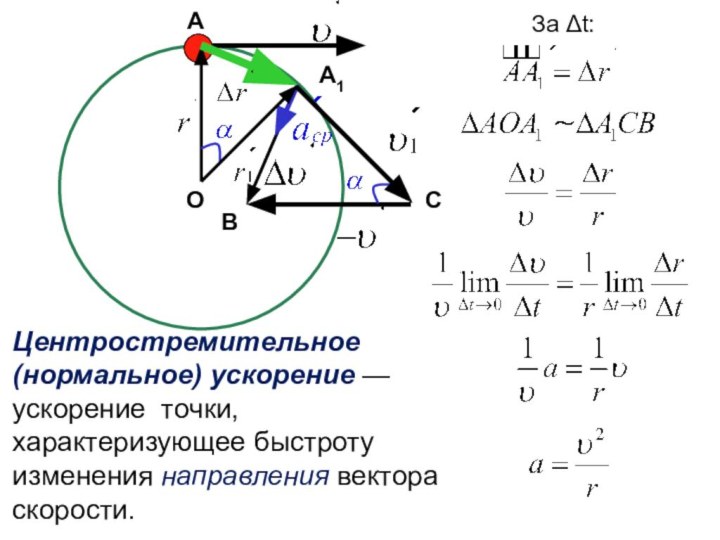
За Δt:
Центростремительное (нормальное) ускорение — ускорение точки, характеризующее быстроту
изменения направления вектора скорости.
Слайд 10
А
А1
О
С
В
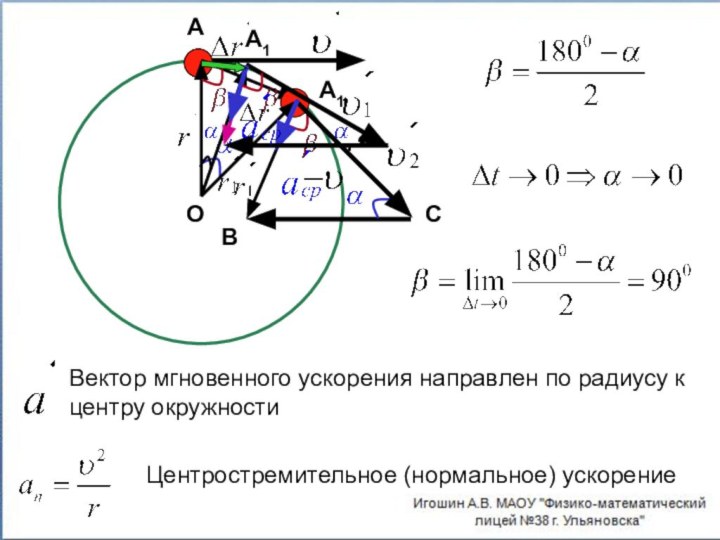
Вектор мгновенного ускорения направлен по радиусу к центру
окружности
Центростремительное (нормальное) ускорение
А1
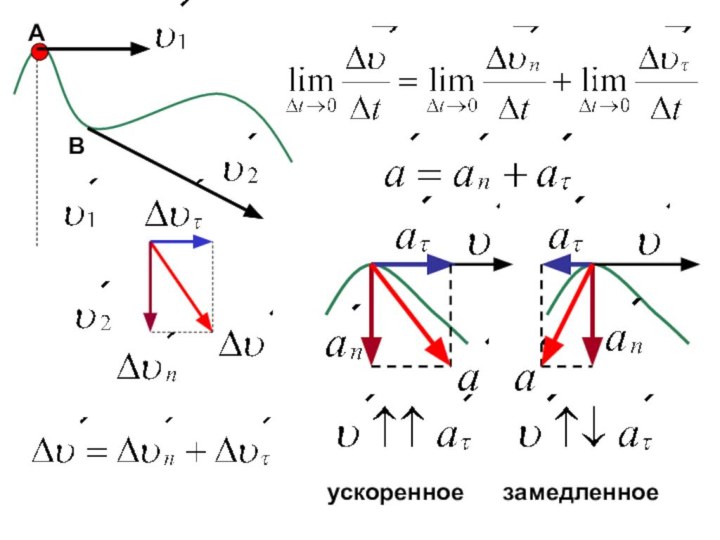
Слайд 12 Если тело движется по окружности неравномерно, то появляется
касательная (тангенциальная) составляющая ускорения.
Касательное (тангенциальное) ускорение характеризует быстроту изменения
модуля вектора скорости.Полное ускорение равно векторной сумме нормального и тангенциального ускорений.
Слайд 15
А
А1
О
x
Радиус-вектор точки – это вектор, начало которого совпадает с
началом системы координат, а конец - с данной точкой.
φ-
угол поворота радиус-вектораРавномерное прямолинейное движение (аналогия)
Слайд 16 Угловой скоростью при равномерном движении по окружности называется
отношение угла поворота Δφ радиус-вектора к промежутку времени Δt,
за который этот оборот произошел.За один полный оборот Δφ=2π, Δt=Т.
Угловая скорость характеризует быстроту изменения угла поворота.
Слайд 18 Угловое ускорение величина, характеризующая быстроту изменения угловой скорости
точки.
Угловым ускорением при равнопеременном движении по окружности называется отношение
изменения угловой скорости Δω к промежутку времени Δt, за которое это изменение произошло.Равнопеременное прямолинейное движение (аналогия)
Слайд 19
Скорость при равнопеременном движении по окружности
ускоренное
замедленное
Равнопеременное прямолинейное движение
(аналогия)
Слайд 20
Уравнение равнопеременного движения точки по окружности
ускоренное
замедленное
Равнопеременное прямолинейное движение
