- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к проектно - исследовательской работе по физике Математический маятник
Содержание
- 2. ВВЕДЕНИЕ В этом году, изучая тему «Механические
- 3. ЦЕЛЬ ИССЛЕДОВАНИЯ Изучить теоретические основы колебательного движения,
- 4. ЗАДАЧИ ИССЛЕДОВАНИЯИзучить учебную литературу о колебаниях.Проследить историю маятников.Изучить методику проведения экспериментов.Провести эксперименты и сделать выводы.
- 5. ЭТАПЫ ИССЛЕДОВАНИЯ: Изучение и анализ литературы по этой теме.Проведение экспериментов.Систематизация работыПодбор наглядного материала. Написание работы.
- 6. ГИПОТЕЗА Если провести эксперименты с математическим маятником, возможно ли определить собственный рост?
- 7. ОБЪЕКТ ИССЛЕДОВАНИЯ: МАТЕМАТИЧЕСКИЙ МАЯТНИК
- 8. ГАЛИЛЕО ГАЛИЛЕЙ (1564-1642) Великий итальянский ученый –
- 9. Сохранилось предание о том, как молодой студент
- 10. ГЮЙГЕНС ХРИСТИАН (1629 – 1695)Формула периода
- 11. В 1656 году в возрасте 27 лет
- 12. МАТЕМАТИЧЕСКИЙ МАЯТНИККолебательную систему образуют: нить с прикрепленным
- 13. ИЛЛЮСТРАЦИЯ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ НА ПРИМЕРЕ МАЯТНИКА ФУКО
- 14. ИССЛЕДОВАНИЕ 1В работе я также решил проверить,
- 15. ИССЛЕДОВАНИЕ 2Нахождение роста с помощью математического маятника по формуле:
- 16. Сначала я отложил свой рост. Я подошел
- 17. Я отсчитал время за 10 колебаний.
- 18. По формуле я начал производить расчёты, но
- 19. ВЫВОДЫ: С помощью нитяного маятника
- 20. ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ КОЛЕБАНИЙ МАЯТНИКА
- 21. ЭТО ИНТЕРЕСНО…О маятнике, его роли и влиянии
- 22. ЛИТЕРАТУРА1. Блудов М.И., Беседы по физике. М.: Просвещение,
- 23. Скачать презентацию
- 24. Похожие презентации
ВВЕДЕНИЕ В этом году, изучая тему «Механические колебания», мы рассматривали колебательные движения на примере двух маятников – нитяного и пружинного. Узнали, какими основными физическими величинами характеризуется колебательное движение: периодом, частотой и амплитудой. Формулы периодов были даны






















Слайд 3
ЦЕЛЬ ИССЛЕДОВАНИЯ
Изучить теоретические основы колебательного движения, провести
опыты и измерения, выявляющих, от чего и как зависит,
период нитяного маятника.
Слайд 4
ЗАДАЧИ ИССЛЕДОВАНИЯ
Изучить учебную литературу о колебаниях.
Проследить историю маятников.
Изучить
методику проведения экспериментов.
Провести эксперименты и сделать выводы.
Слайд 5
ЭТАПЫ ИССЛЕДОВАНИЯ:
Изучение и анализ литературы по этой теме.
Проведение
экспериментов.
Систематизация работы
Подбор наглядного материала. Написание работы.
Слайд 6
ГИПОТЕЗА
Если провести эксперименты с математическим маятником, возможно ли
определить собственный рост?
Слайд 8
ГАЛИЛЕО ГАЛИЛЕЙ
(1564-1642)
Великий итальянский ученый – один из создателей
точного естествознания.
Родился в городе Пизе. Учился сначала
в монастырской школе, а затем в университете. Уже в студенческие годы Галилей увлекся изучением колебаний. Он обнаружил, что колебания маятника не зависят от его массы, а определяются длиной подвеса. Слайд 9 Сохранилось предание о том, как молодой студент медицинского
факультета Галилео Галилей в одно из воскресений 1583 года
с интересом следил за качаниями зажженных лампад в церкви. По ударам пульса он определил время, необходимое для полного размаха лампад. С этого времени медицину пришлось ему оставить и сосредоточиться на физике.Здание Пизанского университета
Слайд 10
ГЮЙГЕНС ХРИСТИАН (1629 – 1695)
Формула периода колебаний
математического маятника впервые была получена на опыте голландским ученым
Х. Гюйгенсом, современником И. Ньютона.Слайд 11 В 1656 году в возрасте 27 лет Гюйгенсом
были сконструированы первые маятниковые часы со спусковым механизмом. Создание
часов, измеряющих время с невиданной точностью, имело далеко идущие последствия для развития физического эксперимента и практической деятельности человека. До этого, время измеряли по истечению воды, горению факела или свечи.
Слайд 12
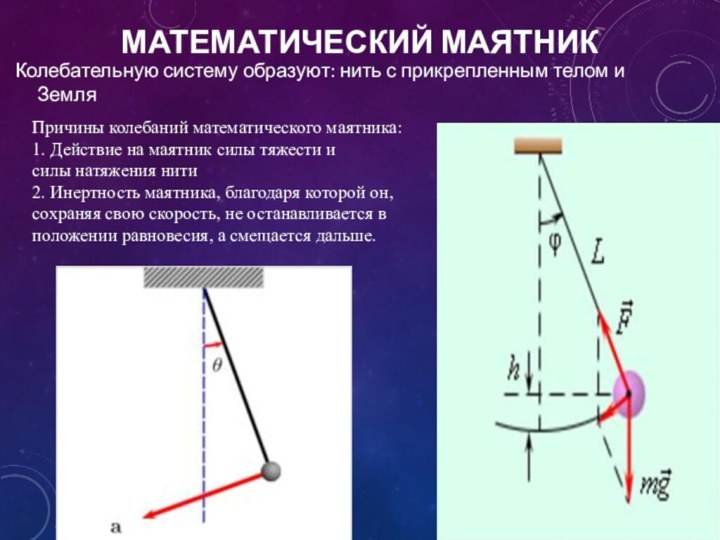
МАТЕМАТИЧЕСКИЙ МАЯТНИК
Колебательную систему образуют: нить с прикрепленным телом
и Земля
Причины колебаний математического маятника:
1. Действие на маятник силы
тяжести и силы натяжения нити
2. Инертность маятника, благодаря которой он, сохраняя свою скорость, не останавливается в положении равновесия, а смещается дальше.
Слайд 13
ИЛЛЮСТРАЦИЯ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ НА ПРИМЕРЕ МАЯТНИКА ФУКО
Маятник
Фуко находится в Исаакиевском соборе и о служит для
демонстрации вращения Земли вокруг своей оси. Вначале опыт был выполнен в узком кругу, но так заинтересовал Наполеона III, французского императора, что он предложил Фуко повторить его публично в грандиозном масштабе под куполом Пантеона в Париже. Эту публичную демонстрацию, устроенную в 1851 году, и принято называть опытом Фуко.
Слайд 14
ИССЛЕДОВАНИЕ 1
В работе я также решил проверить, как
влияет среда на колебания. Измерили время, за которое колебания
затухают в воздухе, а затем опустил маятник в воду и снова измерили период его колебаний и время затухания.Так как маятник качается в мало сопротивляющейся среде, то, казалось бы, нет причины, которая могла бы заметно изменить скорость его качания. Между тем опыт показывает, что маятник в таких условиях качается медленнее (практически не качается), чем это может быть объяснено сопротивлением среды.
Это загадочное на первый взгляд явление объясняется выталкивающим действием воды на погруженные в нее тела. Оно как бы уменьшает вес маятника, не изменяя его массы. Значит, маятник в воде находится совершенно в таких же условиях, как бы он был перенесен на другую планету, где ускорение силы тяжести слабее. Отсюда следует, что с уменьшением ускорения силы тяжести время колебания должно уменьшится: маятник будет колебаться медленнее.
Слайд 16
Сначала я отложил свой рост.
Я подошел к
двери, и сделал отметку.
Затем я отрезал нить такой
же длины, что и мой рост, прикрепил к ней грузик и подвесил в дверном проёме.Слайд 18 По формуле я начал производить расчёты, но с
первого раза у меня не вышло, т.к. маятник был
отклонён на большой угол.Но с третьего раза у меня получилось 1,67 м.
Расчеты верны так, как мой рост 167 см
Слайд 19
ВЫВОДЫ:
С помощью нитяного маятника можно измерить свой
рост, но чтобы правильно получились данные, нужно достаточно точно
произвести расчёты(период и время) и правильно подставить значения в формулу.Период нитяного маятника зависит от длины т.е чем короче нить тем быстрее будет двигаться маятник.
Слайд 20
ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ КОЛЕБАНИЙ МАЯТНИКА
Маятники
используют для регулировки хода часов, поскольку любой маятник имеет
вполне определённый период колебаний.Ускорение свободного падения меняется с географической широтой, так как плотность земной коры различна. В районах, где залегают плотные породы, ускорение несколько больше. Прибор с маятником применили для разведки полезных ископаемых. Подсчитав число качаний, можно обнаружить в земных недрах руды или уголь. С помощью математического маятника измерил свой рост.
Слайд 21
ЭТО ИНТЕРЕСНО…
О маятнике, его роли и влиянии на
жизнь и судьбу человека, писали многие философы и великие
ученые: Аристотель, Плутарх, Платон, Сократ, Архимед.С помощью маятника однажды удалось отыскать пропавшего ребенка. Это произошло в 1934 году. Малыша на глазах у многих свидетелей унес орел. После того как полицией были предприняты безуспешные попытки отыскать его, было решено прибегнуть к помощи маятника, который стали раскачивать над картой, и в том месте, где амплитуда его колебаний достигла максимальной силы, было решено искать ребенка. К удивлению многих, именно там и оказался пропавший мальчик. Эти сенсационные факты были опубликованы в швейцарской газете «Трибюн де Женев».
Слайд 22
ЛИТЕРАТУРА
1. Блудов М.И., Беседы по физике. М.: Просвещение, 2001
г.
2. Кабардин О.Ф., Факультативный курс физики 8 класс. М.: Просвещение,
2009.3. Перельман Я. И., Знаете ли вы физику? Домодедово «ВАП», 2000г.
4. Перышкин А.В., Физика 9 класс. М.:Дрофа 2014г
5. Пинский А.А., Физика и астрономия. М.: Просвещение, 2010 г.
6. Рабиза Ф., Простые опыты. М.: Детская литература 2009 г..