Слайд 2
Тема 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ
1.1. Основные понятия и определения
молекулярной физики и термодинамики
1.2. Давление. Основное уравнение молекулярно-кинетической теории
1.3.
Температура и средняя кинетическая энергия теплового движения молекул
1.4. Законы идеальных газов
1.5. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
Слайд 4
1.1. Основные понятия и определения
молекулярной
физики и термодинамики
Слайд 5
1.1. Основные понятия и определения молекулярной
физики и термодинамики
Совокупность
тел, составляющих макроскопическую систему, называется термодинамической системой.
Система может находиться
в различных состояниях. Величины, характеризующие состояние системы, называются параметрами состояния: давление P, температура T, объём V и так далее. Связь между P, T, V специфична для каждого тела и называется уравнением состояния.
Слайд 7
Любой параметр, имеющий определённое значение для каждого равновесного
состояния, является функцией состояния системы.
Равновесной, называется такая система,
параметры состояния которой одинаковы во всех точках системы и не изменяются со временем (при неизменных внешних условиях). При этом в равновесии находятся отдельные, макроскопические части системы.
Слайд 8
Процесс – переход из одного равновесного состояния
в другое.
Релаксация – возвращение системы в равновесное состояние.
Время перехода – время релаксации.
Слайд 9
Если равновесие установилось, то система самопроизвольно не сможет
выйти из него.
Например, если опустить горячий камень в
холодную воду, то, через некоторое время наступит равновесное состояние: температуры выровняются. Но обратный процесс невозможен – температура камня самопроизвольно не увеличится.
Слайд 10
Атомная единица массы (а.е.м.) – (mед) – единица
массы, равная 1/12 массы изотопа углерода 12С – mC:
Атомная масса химического элемента (атомный вес) А, есть отношение массы атома этого элемента mA к 1/12 массы изотопа углерода С12
(атомная масса – безразмерная величина).
Слайд 11
Молекулярная масса (молекулярный вес):
Отсюда можно найти массу
атома и молекулы в килограммах:
Слайд 12
В термодинамике широко используют понятия киломоль, моль, число
Авогадро и число Лошмидта. Дадим определения этих величин.
Моль – это стандартизированное количество любого вещества, находящегося в газообразном, жидком или твердом состоянии.
1 моль – это количество грамм вещества, равное его молекулярной массе.
Слайд 13
1 киломоль - это количество килограмм
вещества, равное его молекулярной массе.
1 моль – это количество
грамм вещества, равное его молекулярной массе.
Авогадро Амедео (1776 – 1856) –
итальянский физик и химик.
Основные физические работы
посвящены молекулярной физике.
Уже первыми своими исследованиями в этой области заложил основы молекулярной теории, выдвинув молекулярную гипотезу. Открыл важный для химии и физики закон, по которому в равных объемах различных газов при одинаковых условиях содержится одинаковое количество молекул (закон Авогадро). Исходя из этого закона, разработал метод определения молекулярного и атомного весов.
Слайд 15
В 1811 г. Авогадро высказал предположение, что число
частиц в киломоле любого вещества постоянно и равно величине,
названной, в последствии, числом Авогадро
Молярная масса – масса одного моля (µ)
Слайд 16
При одинаковых температурах и давлениях все газы содержат
в единице объёма одинаковое число молекул.
Число молекул идеального
газа, содержащихся в 1 м3 при нормальных условиях, называется числом Лошмидта:
Нормальные условия: P0 = 105 Па; Т0 = 273 К;
k = 1,38·1023 Дж/К – постоянная Больцмана.
Слайд 18
Под идеальным газом мы будем
понимать газ, для которого:
- радиус взаимодействия двух
молекул много меньше среднего расстояния между ними (молекулы взаимодействуют только при столкновении);
- столкновения молекул между собой и со стенками сосуда – абсолютно упругие (выполняются законы сохранения энергии и импульса);
- объем всех молекул газа много меньше объема, занятого газом.
Слайд 19
Следует помнить, что классические представления в молекулярно-кинетической теории
и термодинамике, как и вообще в микромире, не объясняют
некоторые явления и свойства. Здесь, как и в механике, условием применимости классических законов является выполнение неравенства
,
где m – масса, υ – скорость, R – размер пространства движения частицы,
ћ = 1,05·10–34 кг·м2/с – постоянная Планка.
В противном случае используются квантово-механические представления.
Слайд 20
1.2. Давление. Основное уравнение молекулярно-кинетической теории
Рассмотрим подробнее, что представляет собой один из
основных параметров состояния – давление P.
Ещё в XVIII веке Даниил Бернулли предположил, что давление газа – есть следствие столкновения газовых молекул со стенками сосуда.
Именно давление чаще всего является единственным сигналом присутствия газа.
Слайд 21
Итак, находящиеся под давлением газ
или жидкость действуют с некоторой силой на любую поверхность,
ограничивающую их объем. В этом случае сила действует по нормали к ограничивающей объем поверхности. Давление на поверхность равно:
где ΔF – сила, действующая на поверхность площадью ΔS.
Слайд 23
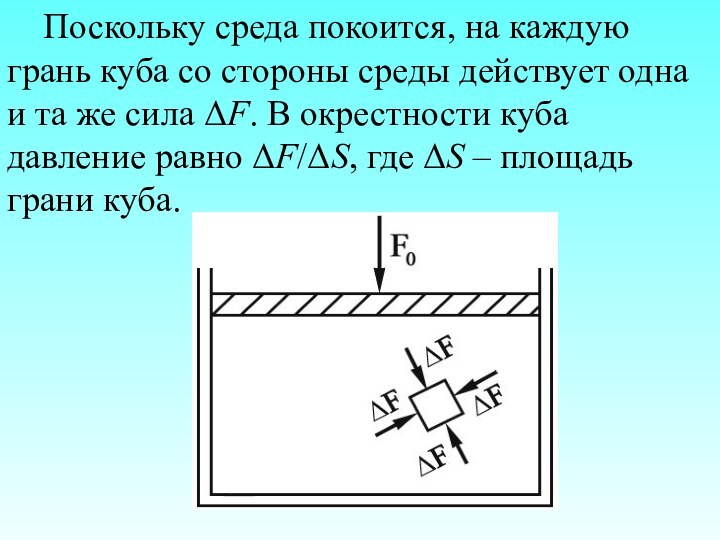
Давление внутри газа или жидкости можно измерить, помещая
туда небольшой куб с тонкими стенками, наполненный той же
средой.
Рисунок 1.1
Слайд 24
Поскольку среда покоится, на каждую грань куба со
стороны среды действует одна и та же сила ΔF.
В окрестности куба давление равно ΔF/ΔS, где ΔS – площадь грани куба.
Слайд 25
Внутреннее давление является одним
и тем же во всех направлениях, и, во всем
объеме независимо от формы сосуда.
Этот результат называется законом Паскаля: если к некоторой части поверхности, ограничивающей газ или жидкость, приложено давление P0, то оно одинаково передается любой части этой поверхности.
Слайд 26
Допустим, автомобиль поднимается гидравлическим домкратом, состоящим, как показано
на рисунке 1.2, из двух соединенных трубкой цилиндров с
поршнями. Диаметр большого цилиндра равен 1 м, а диаметр малого – 10 см. Автомобиль имеет вес F2. Найдем силу давления на поршень малого цилиндра, необходимую для подъема автомобиля.
Слайд 27
Поскольку оба поршня являются стенками одного и того
же сосуда, то в соответствии с законом Паскаля они
испытывают одинаковое давление.
Пусть
– давление на малый поршень, а
– давление на большой поршень.
Тогда, т.к. P1 = P2, имеем:
Слайд 28
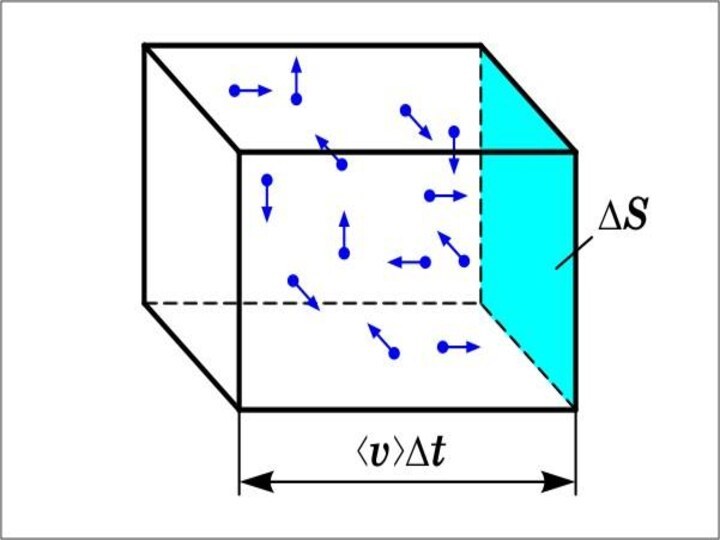
Вычислим давление, оказываемое газом на
одну из стенок сосуда.
Рис. 1.3
Обозначим: n – концентрация молекул в сосуде; m0 – масса одной молекулы. Движение молекул по всем осям равновероятно, поэтому к одной из стенок сосуда, площадью S подлетает в единицу времени молекул, где – проекция вектора скорости на направление, перпендикулярное стенке.
Слайд 31
Каждая молекула обладает импульсом m0υx, но стенка получает
импульс (при абсолютно-упругом
ударе ). За время dt о стенку площадью S успеет удариться число молекул, которое заключено в объёме V:
Общий импульс, который получит стенка S:
Разделив обе части равенства на S и dt; получим выражение для давления:
(1.2.1)
Слайд 32
Таким образом, мы определили давление, как силу, действующую
в единицу времени на единицу площади:
(1.2.2)
Слайд 33
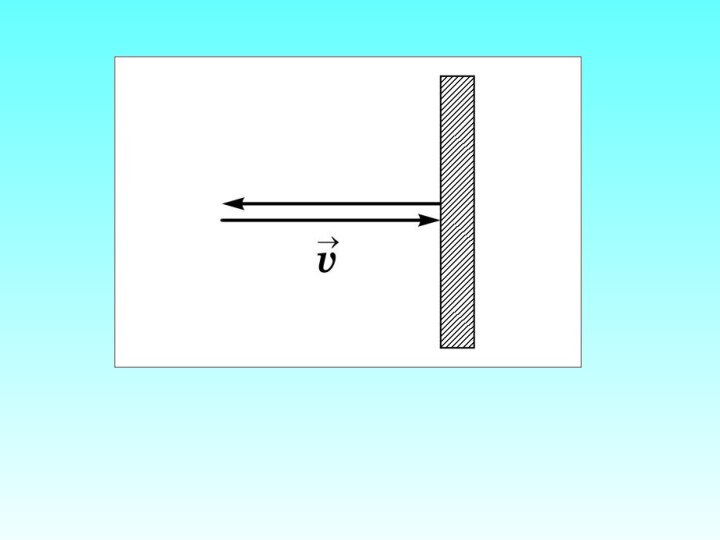
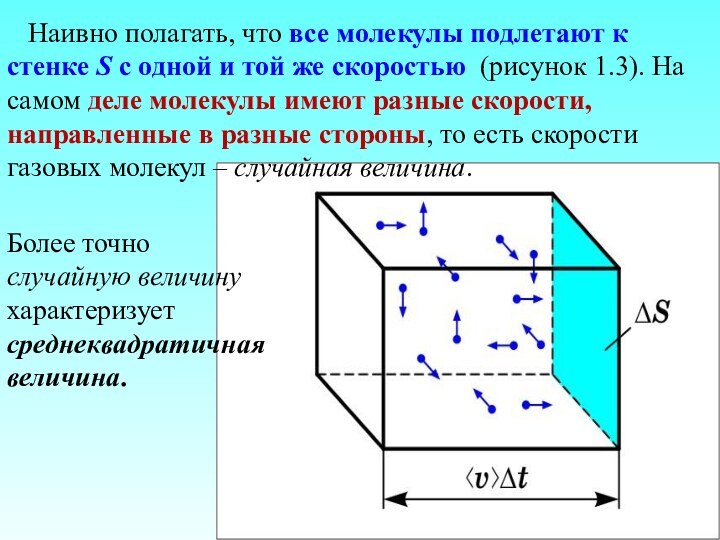
Наивно полагать, что все молекулы подлетают
к стенке S с одной и той же скоростью
(рисунок 1.3). На самом деле молекулы имеют разные скорости, направленные в разные стороны, то есть скорости газовых молекул – случайная величина.
Более точно случайную величину характеризует среднеквадратичная величина.
Слайд 34
Под скоростью понимаем
среднеквадратичную скорость
Вектор скорости,
направленный произвольно в пространстве, можно разделить на три составляющих:
Ни одной из этих проекций нельзя отдать предпочтение из-за хаотичного теплового движения молекул, то есть в среднем .
Слайд 35
Следовательно, на другие стенки будет точно такое же
давление. Тогда можно записать в общем случае:
или
(1.2.3)
где – средняя энергия одной молекулы. Это основное уравнение молекулярно-кинетической теории газов.
Итак, давление газов определяется средней кинетической энергией поступательного движения молекул.
Слайд 36
Единицы измерения давления.
По определению,
поэтому
размерность
давления
1 Н/м2 = 1Па;
1 атм.= 9,8 Н/см2 = 98066 Па 105 Па
1 мм рт.ст. = 1 тор = 1/760 атм. = 133,3 Па
1 бар = 105 Па; 1 атм. = 0,98 бар.
Слайд 37
1.3. Температура и средняя кинетическая энергия теплового
движения молекул
Из опыта известно, что если привести
в соприкосновение два тела: горячее и холодное, то через некоторое время их температуры выровняются. Что перешло от одного тела к другому?
Раньше, во времена Ломоносова и Лавуазье считали, что носителем тепла является некоторая жидкость – теплород.
На самом деле – ничего не переходит, только изменяется средняя кинетическая энергия – энергия движения молекул, из которых состоят эти тела.
Слайд 38
Именно средняя кинетическая энергия атомов и молекул
служит характеристикой системы в состоянии равновесия.
Это свойство
позволяет определить параметр состояния, выравнивающийся у всех тел, контактирующих между собой, как величину, пропорциональную средней кинетической энергии частиц в сосуде.
Слайд 39
Чтобы связать энергию с температурой, Больцман ввел коэффициент
пропорциональности k, который впоследствии был назван его именем:
(1.3.1)
где k – постоянная Больцмана
k = 1,38·1023 Дж·К1.
Слайд 40
Величину T называют абсолютной темпе-ратурой и измеряют в
градусах Кельвина (К). Она служит мерой кинетической энергии теплового
движения частиц идеального газа. Из (1.3.1) получим:
(1.3.2)
Формула (1.3.2) применима для расчетов на одну молекулу идеального газа.
Обозначим
где R – универсальная газовая постоянная:
Слайд 41
Тогда
следовательно,
(1.3.3)
– это формула для молярной массы газа.
Слайд 42
Так как температура определяется средней энергией
движения молекул, то она, как и давление, является статистической
величиной, то есть параметром, проявляющимся в результате совокупного действия огромного числа молекул. Поэтому не говорят: «температура одной молекулы», нужно сказать: «энергия одной молекулы, но температура газа».
Слайд 43
Основное уравнение молекулярно-кинетической теории можно записать по другому.
Так как
Отсюда
В таком виде основное уравнение молекулярно-кинетической теории
употребляется чаще.
Слайд 44
Термометры. Единицы измерения температуры
Наиболее естественно было
бы использовать для измерения температуры определение
т.е. измерять кинетическую энергию поступательного движения молекул газа. Однако чрезвычайно трудно проследить за молекулой газа и еще сложнее за атомом. Поэтому для определения температуры идеального газа используется уравнение
Слайд 45
Действительно, величины P и V легко поддаются измерению.
В
качестве примера рассмотрим изображенный на рисунке 1.4 простейший газовый
термометр с постоянным давлением. Объем газа в трубке
как мы видим, пропорционален температуре, а поскольку высота подъема ртутной капли пропорциональна V, то она пропорциональна и Т.
Слайд 47
Существенно то, что в газовом термометре необходимо использовать
идеальный газ. Если же в трубку вместо идеального газа
поместить фиксированное количество жидкой ртути, то мы получим обычный ртутный термометр. Хотя ртуть далеко не идеальный газ, вблизи комнатной температуры ее объем изменяется почти пропорционально температуре. Термометры, в которых вместо идеального газа используются какие-либо другие вещества, приходится калибровать по показаниям точных газовых термометров.
Слайд 48
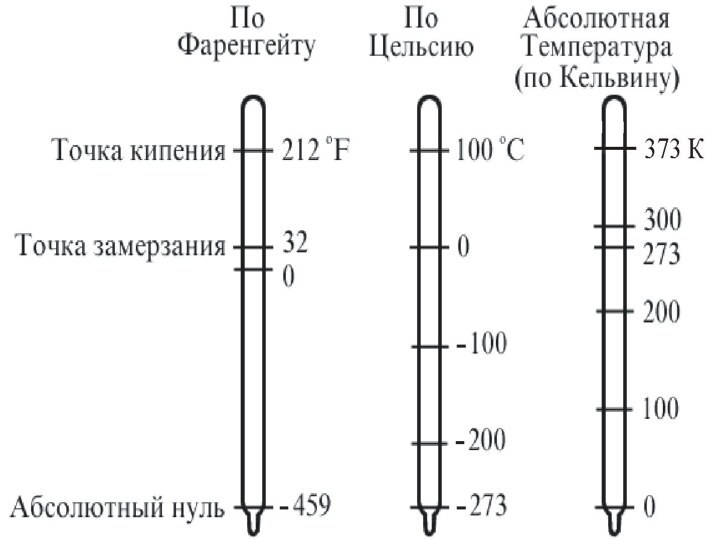
В физике и технике за абсолютную шкалу температур
принята шкала Кельвина, названная в честь знаменитого английского физика,
лорда Кельвина.
1 К – одна из основных единиц системы СИ
Кроме того, используются и другие шкалы:
– шкала Фаренгейта (немецкий физик 1724 г.) – точка таянья льда 32F, точка кипения воды 212F.
– шкала Цельсия (шведский физик 1842г.) – точка таянья льда 0С, точка кипения воды 100С.
0С = 273,15 К.
На рис.1.5приведено сравнение разных темп. шкал.
Цельсий Андерс (1701 – 1744)
– шведский астроном и физик.
Работы относятся к астрономии,
геофизике, физике. Предложил в 1742 г. стоградусную шкалу термометра, в которой за ноль градусов принял температуру таяния льда, а за 100 градусов – температуру кипения воды.
всегда, то и Т
не может быть отрицательной величиной.
Своеобразие температуры заключается в том, что она не аддитивна (аддитивный – получаемый сложением).
Если мысленно разбить тело на части, то температура всего тела не равна сумме температур его частей (длина, объём, масса, сопротивление, и так далее – аддитивные величины). Поэтому температуру нельзя измерять, сравнивая её с эталоном.
Слайд 52
Современная термометрия основана на шкале идеального газа, где
в качестве термометрической величины используют давление. Шкала газового термометра
– является абсолютной (Т = 0; Р = 0).
Слайд 54
1.4. Законы идеальных газов
В XVII –
XIX веках были сформулированы опытные законы идеальных газов, которые
подробно изучаются в школьном курсе физики. Кратко напомним их.
Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.
Слайд 55
1.Изохорический процесс. V = const.
Изохорическим процессом называется процесс,
протекающий при постоянном объёме V.
Поведение газа при этом
изохорическом процессе подчиняется закону Шарля: P/Т = const:
«При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным».
Слайд 56
График изохорического процесса на РV диаграмме называется изохорой.
Полезно знать график изохорического процесса на РТ и VT
диаграммах (рисунок 1.6).
Слайд 57
Уравнение изохоры:
(1.4.1)
Если температура газа выражена в градусах Цельсия, то уравнение изохорического процесса записывается в виде
(1.4.2)
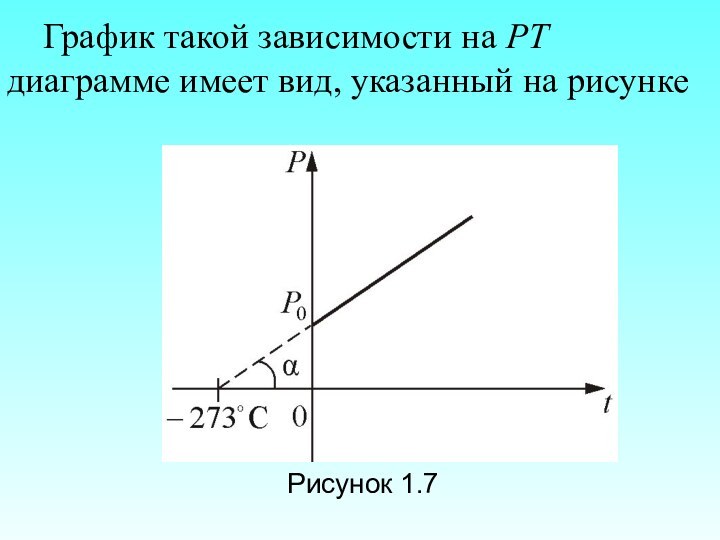
где Р0 – давление при 0С по Цельсию; α температурный коэффициент давления газа равен 1/273 град1.
Слайд 58
График такой зависимости на РТ диаграмме имеет
вид, указанный на рисунке
Рисунок 1.7
Слайд 59
2. Изобарический процесс. Р = const.
Изобарическим
процессом называется процесс, протекающий при постоянном давлении Р.
Поведение
газа при изобарическом процессе подчиняется закону Гей-Люссака:
V/T = const
«При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным».
Слайд 60
Жозеф Гей-Люссак
Французский химик и физик, член АН в
Париже (1806).
Слайд 61
График изобарического процесса на VT диаграмме называется изобарой
(рис. 1.8). Полезно знать графики изобарического процесса на РV
и РT диаграммах.
Рисунок 1.8
Слайд 62
Уравнение изобары
(1.4.3)
Если температура газа выражена в градусах Цельсия, то уравнение изобарического процесса записывается в виде
(1.4.4)
где температурный коэффициент объёмного расширения.
Слайд 63
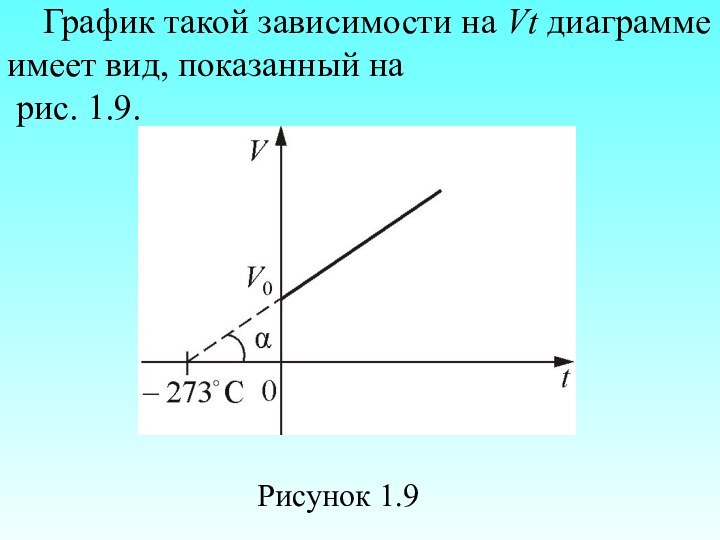
График такой зависимости на Vt диаграмме имеет вид,
показанный на
рис. 1.9.
Рисунок 1.9
Слайд 64
3. Изотермический процесс. T = const.
Изотермическим процессом называется
процесс, протекающий при постоянной температуре Т.
Поведение идеального
газа при изотермическом процессе подчиняется закону Бойля-Мариотта:
РV = const
«При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным».
График изотермического процесса на РV – диаграмме называется изотермой.
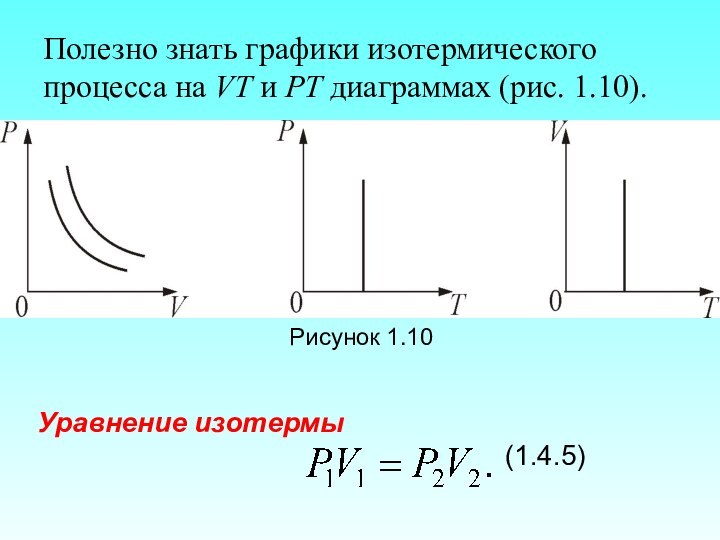
Слайд 66
Полезно знать графики изотермического процесса на VT и
РT диаграммах (рис. 1.10).
Рисунок 1.10
Уравнение изотермы
(1.4.5)
Слайд 67
4. Адиабатический процесс (изоэнтропийный).
Процесс, происходящий без теплообмена
с окружающей средой.
5. Политропический процесс.
Процесс,
при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.
Слайд 68
6. Закон Авогадро.
При одинаковых давлениях и одинаковых
температурах, в равных объёмах различных идеальных газов содержится одинаковое
число молекул.
В одном моле различных веществ содержится
молекул (число Авогадро).
Слайд 69
7. Закон Дальтона.
Давление смеси идеальных газов равно
сумме парциальных давлений Р, входящих в неё газов
(Р1 – давление, которое оказывал бы определённый газ из смеси, если бы он занимал весь объём).
Слайд 70
8. Объединённый газовый закон (Закон Клапейрона).
В соответствии
с законами Бойля - Мариотта (1.4.5) и Гей-Люссака (1.4.3)
можно сделать заключение, что для данной массы газа
(1.4.7)
Это объединённый газовый закон Клапейрона.
Клапейрон Бенуа Поль Эмиль
(1799 – 1864) – французский
физик и инженер. Физические
исследования посвящены
теплоте, пластичности и равновесию твердых тел. Придал математическую форму идеям Н. Карно, первым оценил большое научное значение его труда. Вывел уравнения состояния идеального газа. Впервые ввел в термодинамику графический метод.
Слайд 72
1.5. Уравнение состояния идеального газа
(уравнение Менделеева-Клапейрона)
Идеальным
газом называют газ, молекулы которого пренебрежимо малы, по сравнению
расстояния между ними, и не взаимодействуют друг с другом на расстоянии.
Все газы, при нормальных условиях, близки по свойствам к идеальному газу. Ближе всех газов к идеальному газу – водород.
Уравнение, связывающее основные параметры состояния идеального газа вывел великий русский ученый Д.И. Менделеев.
Менделеев Дмитрий Иванович
(1834 – 1907) – русский ученый.
Работы преимущественно в области
химии, а также физики, метрологии,
метеорологии. Открыл в 1869 году
один из фундаментальных законов природы – периодический закон химических элементов – и, на его основе, создал периодическую таблицу химических элементов. Исправил значения атомных весов многих элементов, предсказал существование и свойства новых.
Слайд 74
Менделеев объединил известные нам законы Бойля-Мариотта, Гей-Люссака и
Шарля с законом Авогадро. Уравнение, связывающее все эти законы,
называется уравнением Менделеева-Клапейрона и записывается так:
, (1.5.1)
здесь – число молей. Для одного моля можно записать
– плотность газа, то
(1.5.2)
Если рассматривать смесь газов, заполняющих объём V при температуре Т, тогда, парциальные давления, можно найти, как:
, , …..
Слайд 76
Согласно закону Дальтона: полное давление смеси газа
равно сумме парциальных давлений всех газов, входящих в смесь
Отсюда, с учетом вышеизложенного, можно записать
(1.5.3)
– это уравнение Менделеева-Клапейрона для смеси газов.