Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Дифракция света

Содержание

Дифракция Френеля S – точечный источник светаP – точка наблюденияОпределим, чтобудет наблю-даться в т. P.
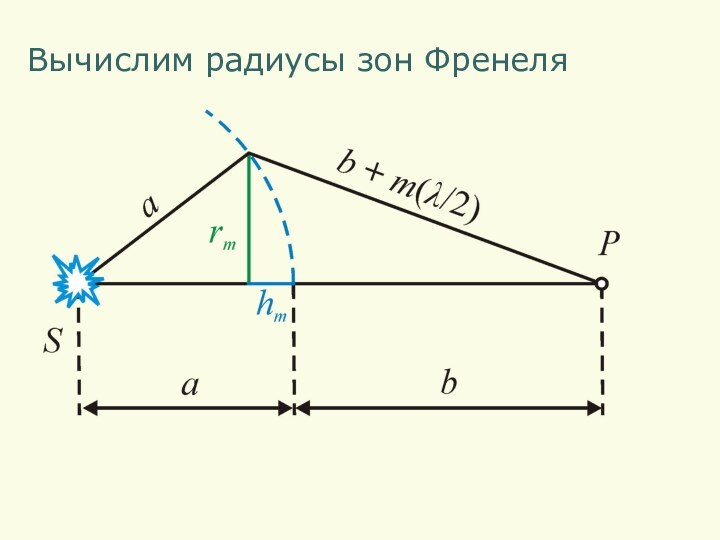
Распространение волнЧасть 2 Дифракция Френеля S – точечный источник светаP – точка Разобьем ВП на кольцевые зоны так,чтобы расстояние от точки P до их Вычислим радиусы зон Френеля – высота сферическогосегмента, занимаемогозоной с номером m– радиус m-ой зоны ФренеляПлощадь сферическогосегмента: Площадь m-ой зоны:т.е. 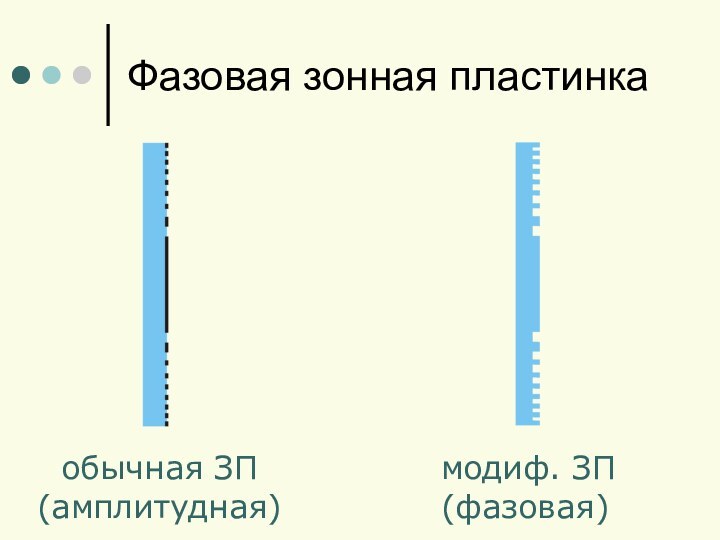площади зон Френеля практическиодинаковы и энергия, переносимаякаждой зоной в отдельности, почти одинакова Вычислим амплитуду в т.P, котораяполучается при сложении всех зони учтем, что зоны находятся в противофазе: Например, радиус первой зоны приa =∞ (плоский в.ф.), b = 1 м Зонная пластинка Фазовая зонная пластинкаобычная ЗП(амплитудная)модиф. 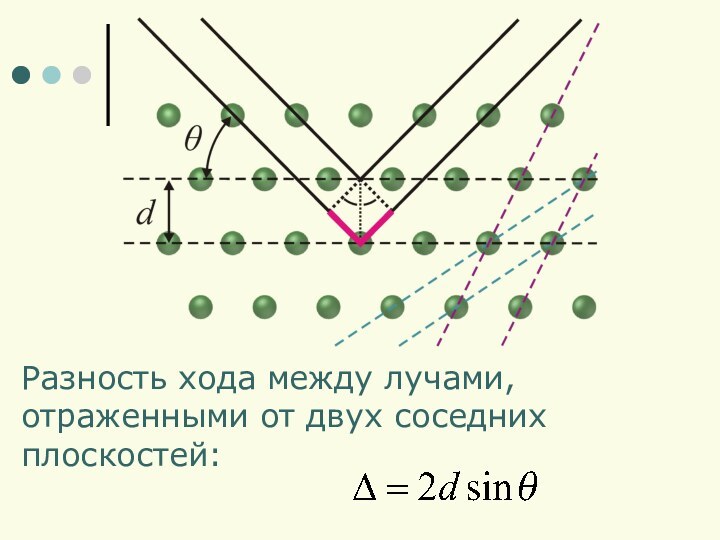ЗП(фазовая) Дифракция рентгеновских лучейЕстественные 3х мерные периодическиеструктуры – кристаллы (d = 1–4 Å Пусть рентгеновское излучение падаетна пространственную решетку.Ю.В.Вульф и англ.физики Брэгги (1913)предложили способ расчета Разобьем кристалл на ряд параллельныхплоскостей (одним из многих способов)d – расстояние м/у Разность хода между лучами,отраженными от двух соседнихплоскостей: Условие наилучшего отражения: Применение явления дифракции света на кристаллах1) В рентгеновской спектроскопии для исследования 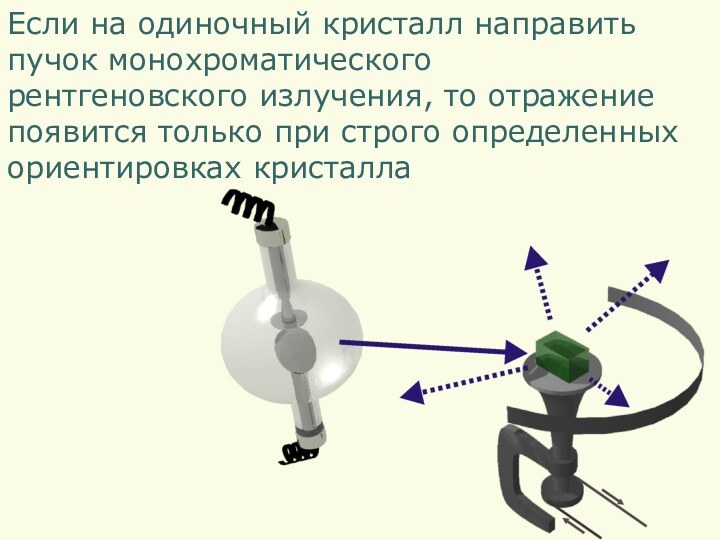Если на одиночный кристалл направитьпучок монохроматического рентгеновского излучения, то отражение появится только 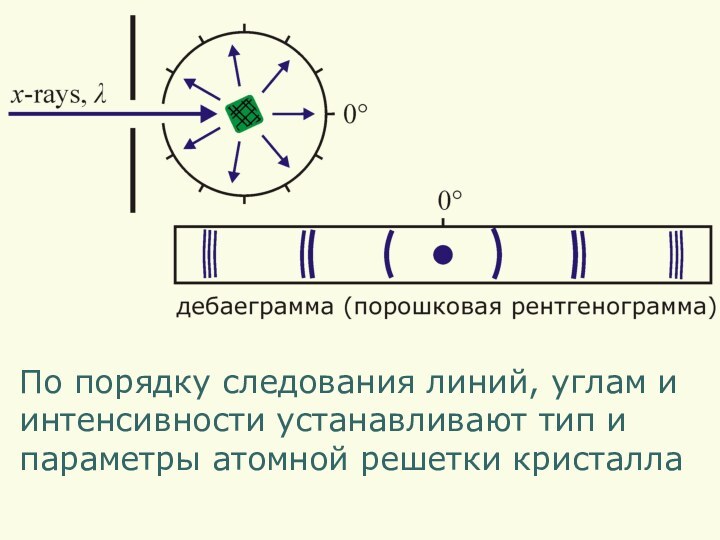Метод порошковЕсли взять поликристаллический образец(много кристалликов, спрессованных илиспеченных), то для любого направлениянаходится По порядку следования линий, углам иинтенсивности устанавливают тип ипараметры атомной решетки кристалла
Слайды презентации

Слайд 2 Дифракция Френеля
S – точечный
источник

Дифракция Френеля S – точечный источник светаP – точка

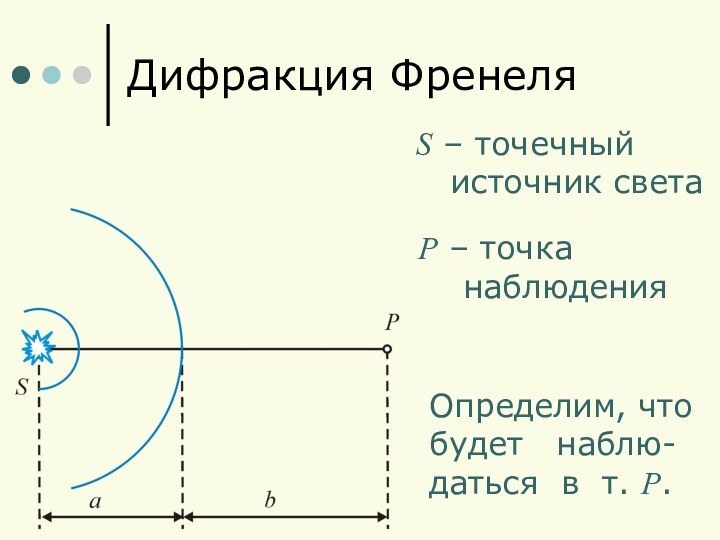
света
P – точка
наблюдения
Определим, что
будет наблю-
даться

в т. P.

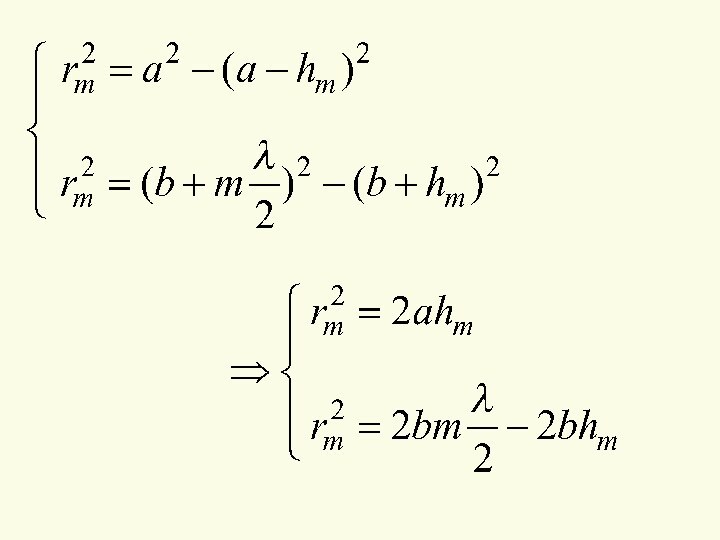
Слайд 3
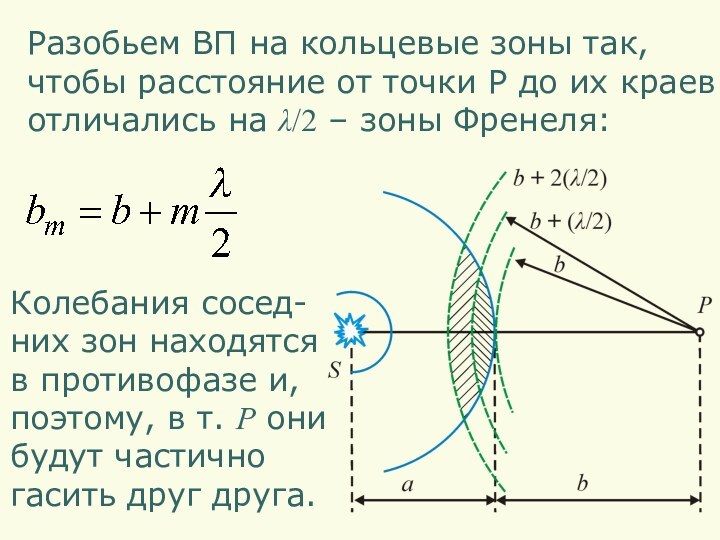
Разобьем ВП на кольцевые зоны так,
чтобы расстояние от

Разобьем ВП на кольцевые зоны так,чтобы расстояние от точки P до

точки P до их краев
отличались на λ/2 –

зоны Френеля:

Колебания сосед-
них зон находятся
в противофазе и,
поэтому, в т. Р они
будут частично
гасить друг друга.

Слайд 4
Вычислим радиусы зон Френеля

Вычислим радиусы зон Френеля

Слайд 5

Слайд 6
– высота сферического
сегмента, занимаемого
зоной с номером m
– радиус

– высота сферическогосегмента, занимаемогозоной с номером m– радиус m-ой зоны ФренеляПлощадь сферическогосегмента:

m-ой зоны
Френеля
Площадь сферического
сегмента:

Слайд 7
Площадь m-ой зоны:
т.е. площади зон Френеля практически
одинаковы и

Площадь m-ой зоны:т.е. площади зон Френеля практическиодинаковы и энергия, переносимаякаждой зоной в отдельности, почти одинакова

энергия, переносимая
каждой зоной в отдельности,
почти одинакова

Слайд 8
Вычислим амплитуду в т.P, которая
получается при сложении всех

Вычислим амплитуду в т.P, котораяполучается при сложении всех зони учтем, что зоны находятся в противофазе:

зон
и учтем, что зоны находятся в
противофазе:

Слайд 9
Например, радиус первой зоны при
a =∞ (плоский в.ф.),

Например, радиус первой зоны приa =∞ (плоский в.ф.), b = 1

b = 1 м получаем
r1 = 0.8 мм.
Следовательно, свет

от ист. S к точке P
распространяется (как бы) в узком
канале, ограниченном первой зоной –
т.е. практически прямолинейно.

При открытии только первой зоны:

Если отверстие в экране открывает и
вторую зону, то интенсивность в т.Р
падает практически до нуля.

Слайд 10 Зонная пластинка

Зонная пластинка

Слайд 11 Фазовая зонная пластинка
обычная ЗП
(амплитудная)
модиф. ЗП
(фазовая)

Фазовая зонная пластинкаобычная ЗП(амплитудная)модиф. ЗП(фазовая)

Слайд 12 Дифракция рентгеновских лучей
Естественные 3х мерные периодические
структуры – кристаллы

Дифракция рентгеновских лучейЕстественные 3х мерные периодическиеструктуры – кристаллы (d = 1–4

(d = 1–4 Å =

= 0.1–0.4 нм)

λвид ~ 500 нм

λрент ~0.01–100 нм

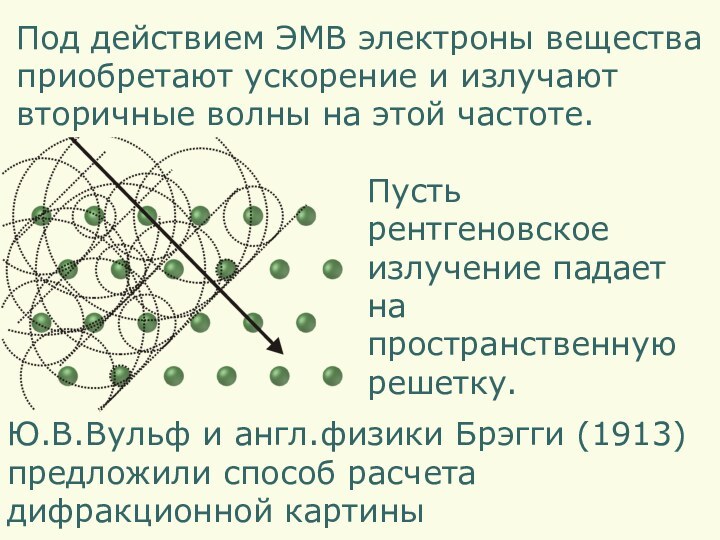
Слайд 13 Пусть
рентгеновское
излучение падает
на
пространственную
решетку.
Ю.В.Вульф и англ.физики

Пусть рентгеновское излучение падаетна пространственную решетку.Ю.В.Вульф и англ.физики Брэгги (1913)предложили способ

Брэгги (1913)
предложили способ расчета
дифракционной картины
Под действием ЭМВ электроны

вещества
приобретают ускорение и излучают
вторичные волны на этой частоте.

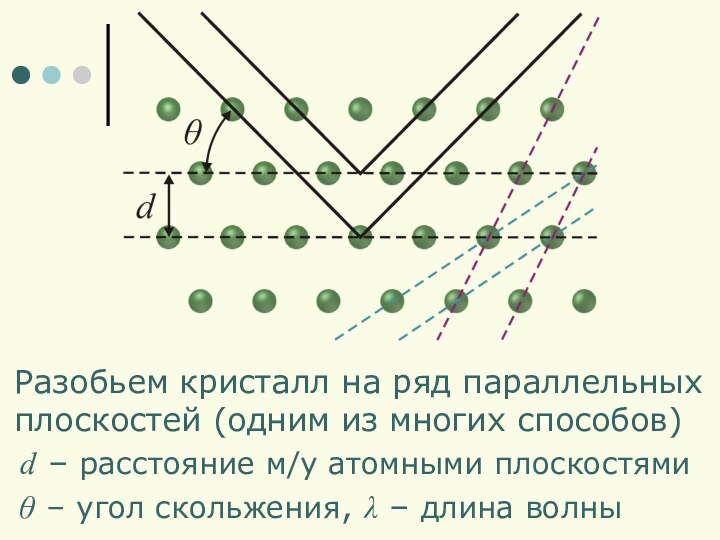
Слайд 14 Разобьем кристалл на ряд параллельных
плоскостей (одним из многих

Разобьем кристалл на ряд параллельныхплоскостей (одним из многих способов)d – расстояние

способов)
d – расстояние м/у атомными плоскостями
θ – угол скольжения,

λ – длина волны

Слайд 15 Разность хода между лучами,
отраженными от двух соседних
плоскостей:

Разность хода между лучами,отраженными от двух соседнихплоскостей:

Слайд 16 Условие наилучшего отражения:

Условие наилучшего отражения:

Слайд 17 Применение явления дифракции света на кристаллах


1) В рентгеновской спектроскопии

Применение явления дифракции света на кристаллах1) В рентгеновской спектроскопии для исследования

для исследования характеристик
излучения
2) В рентгеноструктурном анализе

для изучения внутренней структуры
кристаллов

Слайд 18 Если на одиночный кристалл направить
пучок монохроматического
рентгеновского излучения,

Если на одиночный кристалл направитьпучок монохроматического рентгеновского излучения, то отражение появится

то отражение
появится только при строго определенных
ориентировках кристалла

Слайд 19 Метод порошков
Если взять поликристаллический образец
(много кристалликов, спрессованных или
спеченных),

Метод порошковЕсли взять поликристаллический образец(много кристалликов, спрессованных илиспеченных), то для любого

то для любого направления
находится большое количество правильно
ориентированных атомных плоскостей.

  • Имя файла: difraktsiya-sveta.pptx
  • Количество просмотров: 150
  • Количество скачиваний: 0
- Предыдущая ОСНОВАНИЯ, ИХ КЛАССИФИКАЦИЯ И СВОЙСТВА
Следующая - СЕРДЕЧНО-СОСУДИСТЫЕ ЗАБОЛЕВАНИЯ

Похожие презентации

Работа и мощность электрического тока Работа и мощность электрического тока 132
Физические повреждающие факторы внешней среды Физические повреждающие факторы внешней среды 132
Действие жидкости на погруженное в нее тело. Сила Архимеда Действие жидкости на погруженное в нее тело. Сила Архимеда 120
Как тепловое действие тока помогает в нашем доме? Как тепловое действие тока помогает в нашем доме? 126
Магнитное поле в веществе Магнитное поле в веществе 130
Объяснение электризации тел Объяснение электризации тел 105
Джеймс Клерк Максвелл Джеймс Клерк Максвелл 118
Атмосфера. Атмосферное давление Атмосфера. Атмосферное давление 136
Виды сил 7 класс Виды сил 7 класс 151
Проект по теме Самостоятельная работа на уроках физики Проект по теме Самостоятельная работа на уроках физики 189
Презентация к уроку Рентгеновское излучение Презентация к уроку Рентгеновское излучение 195
Рентгеновское излучение Рентгеновское излучение 175
Давление в технике и строительстве Давление в технике и строительстве 128
Электромагнитные волны Электромагнитные волны 131
Физика и спорт Физика и спорт 148
Физика магнитного поля Физика магнитного поля 109
Свободное падение тел (9 КЛАСС) Свободное падение тел (9 КЛАСС) 149
Звук. Звуковые явления Звук. Звуковые явления 137
Теории прочности Теории прочности 126
Презентация по физике на тему Лазеры (11 класс) Презентация по физике на тему Лазеры (11 класс) 136
Формирование мобильной среды обучения с использованием интернет- сервисов портала ЯКласс. Формирование мобильной среды обучения с использованием интернет- сервисов портала ЯКласс. 133
Нестандартное физкультурное оборудование в ДОУ Нестандартное физкультурное оборудование в ДОУ 195
Термоядерные реакции (9 класс) Термоядерные реакции (9 класс) 139
Российские физики – нобелевские лауреаты Российские физики – нобелевские лауреаты 105
Расчет сопротивления проводника. Удельное сопротивление Расчет сопротивления проводника. Удельное сопротивление 145
Презентация по теме: Скорость. Мгновенная скорость. Презентация по теме: Скорость. Мгновенная скорость. 157
Презентация Миллион кімге бұйырады? Презентация Миллион кімге бұйырады? 240
Паровая турбина (8 класс) Паровая турбина (8 класс) 166
Презентация к открытому уроку по теме: Закон Архимеда Презентация к открытому уроку по теме: Закон Архимеда 144
Интеллектуальное кафе Интеллектуальное кафе 133