- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Динамика материальной точки
Содержание
- 2. 1. Первый закон Ньютона. Инерциальные системы В
- 3. Первый закон Ньютона: всякая материальная точка сохраняет
- 4. Скорость любого тела остаётся постоянной (в частности,
- 5. Первый закон Ньютона выполняется в инерциальных системах
- 6. Система отсчёта, связанная с Землей, строго говоря,
- 7. Сущность первого закона Ньютона может быть сведена
- 8. 2. Масса и импульс тела Воздействие на
- 9. Масса – величина аддитивная (масса тела равна
- 10. Приняв во внимание направление скоростей, запишем:Произведение массы
- 11. 3. Второй закон Ньютона. Математическое
- 13. Найдем изменение импульса тела за конечный промежуток времени изменение импульса тела равно импульсу силы.
- 14. В системе СИ семь основных единиц (м)
- 15. 4. Третий закон Ньютона Действие тел друг на
- 16. Всякое действие вызывает равное по величине противодействие
- 17. 5. Импульс произвольной системы тел
- 18. – импульс системы тел равен произведению массы
- 19. 6. Основное уравнение динамики поступательного движения произвольной системы тел
- 20. Обозначим –
- 21. Сложим эти уравнения и сгруппируем попарно силы
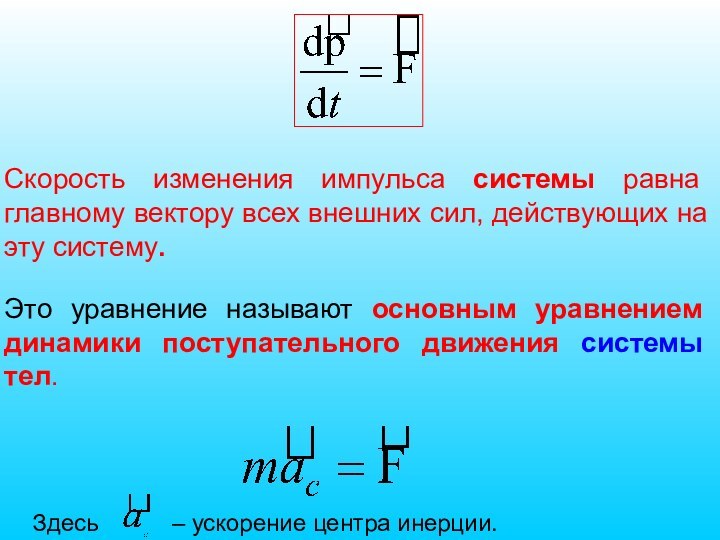
- 22. Скорость изменения импульса системы равна главному вектору
- 23. Центр механической системы движется как материальная точка,
- 24. Теорема о движении центра массСилы, действующие на
- 25. 7. Закон сохранения импульса
- 26. отсюдаимпульс замкнутой системы не изменяется во времени. Импульс
- 28. СИЛЫ В МЕХАНИКЕ
- 29. 1. Виды и категории сил в природе В
- 30. Гравитационные и электромагнитные силы нельзя свести к
- 32. 2. Сила тяжести и вес тела Силы тяжести
- 33. Если подвесить тело или положить его на
- 34. По третьему закону Ньютона тело действует на
- 35. Вес и сила тяжести равны друг другу,
- 36. Вес тела может быть больше или меньше
- 37. 3. Упругие силы Электромагнитные силы проявляют себя как
- 38. Рассмотрим упругие деформации. В деформированном теле возникают упругие силы, уравновешивающие внешние силы.
- 39. Упругие силы возникают во всей деформированной пружине.
- 40. Так как упругая сила отличается от внешней
- 41. Тогда полная работа, которая совершена пружиной, равна:
- 42. 4. Силы трения Трение подразделяется на внешнее и
- 43. Жидким (вязким) называется трение между твердым телом
- 44. Подействуем на тело, внешней силой
- 45. Установлено, что максимальная сила трения покоя не
- 46. 5. Силы инерции 5.1. Уравнение Ньютона для
- 47. С точки зрения наблюдателя на Земле (в
- 49. Силы, действующие со стороны связей могут
- 50. Силы инерции при поступательном движении неинерциальной системы
- 51. Ускорение в инерциальной системе можно выразить через
- 52. где –
- 53. Силы инерции неинвариантны относительно перехода из одной
- 54. Силы инерции при вращательном движении неинерциальной системы отсчета.
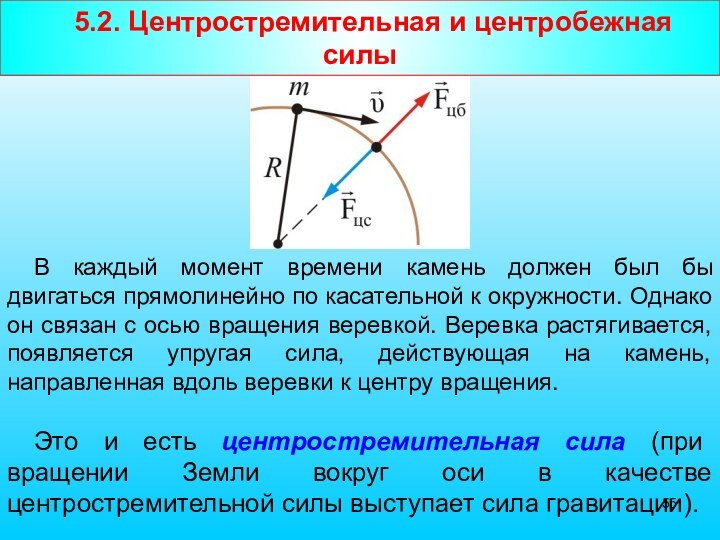
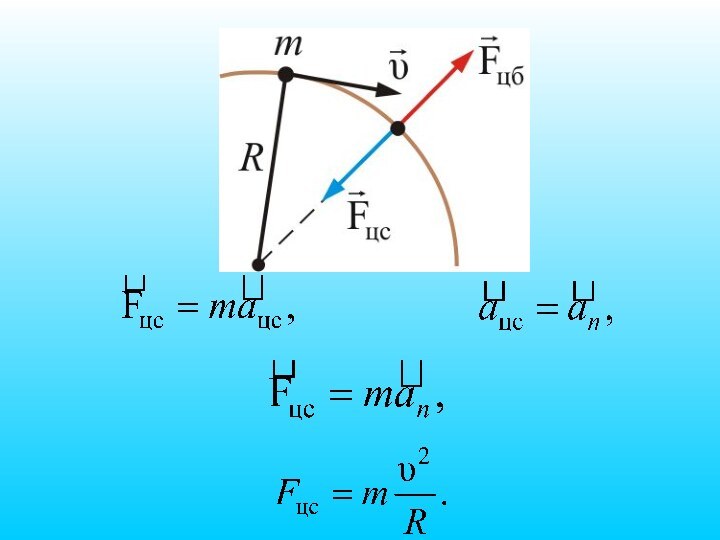
- 55. 5.2. Центростремительная и центробежная силыВ каждый момент
- 56. .
- 57. Центростремительная сила возникла в результате
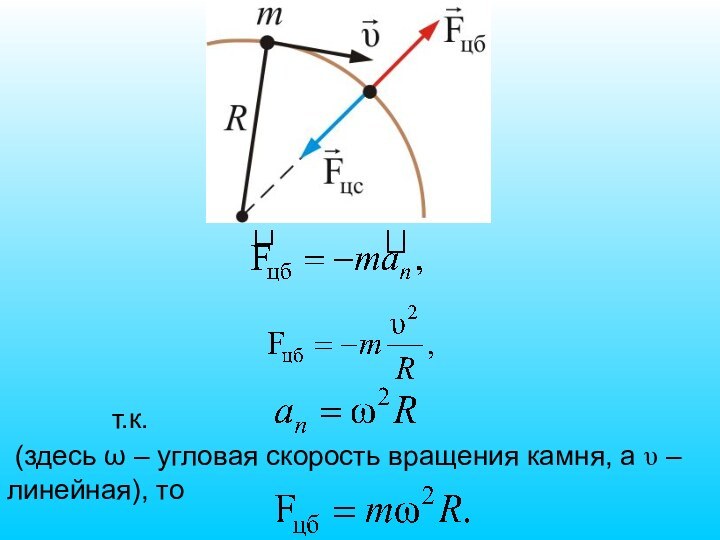
- 58. т.к. (здесь ω – угловая скорость вращения камня, а υ – линейная), то
- 59. 5.3. Сила Кориолиса При движении тела относительно
- 60. Это приводит к тому, что
- 61. Силы Кориолиса проявляются и при качаниях маятника
- 62. Скачать презентацию
- 63. Похожие презентации








































Слайд 3
Первый закон Ньютона:
всякая материальная точка сохраняет состояние
покоя или равномерного прямолинейного движения до тех пор, пока
воздействие со стороны других тел не заставит её изменить это состояние.(Закон инерции)
Слайд 4 Скорость любого тела остаётся постоянной (в частности, равной
нулю), пока воздействие на это тело со стороны других
тел не вызовет её изменения.Стремление тела сохранить состояние покоя или равномерного прямолинейного движения называется инертностью.
Поэтому первый закон Ньютона называют законом инерции.
Слайд 5 Первый закон Ньютона выполняется в инерциальных системах отсчёта.
Инерциальной системой отсчёта является такая система отсчёта, относительно которой
материальная точка, свободная от внешних воздействий, либо покоится, либо движется прямолинейно и равномерно (т.е. с постоянной скоростью).Таким образом, первый закон Ньютона утверждает существование инерциальных систем отсчёта.
Слайд 6 Система отсчёта, связанная с Землей, строго говоря, неинерциальная,
однако эффекты, обусловленные её неинерциальностью (Земля вращается вокруг собственной
оси и вокруг Солнца) при решении многих задач малы, и в этих случаях её можно считать инерциальной.Слайд 7 Сущность первого закона Ньютона может быть сведена к
трём основным положениям:
все тела обладают свойствами инерции;
существуют инерциальные системы
отсчёта, в которых выполняется первый закон Ньютона;движение относительно.
Слайд 8
2. Масса и импульс тела
Воздействие на данное
тело со стороны других тел вызывает изменение его скорости,
т.е. сообщает данному телу ускорение.Опыт показывает, что одинаковое воздействие сообщает разным телам разные по величине ускорения. Всякое тело противится попыткам изменить его состояние движения. Это свойство тел, как мы уже говорили, называется инертностью (следует из первого закона Ньютона).
Мерой инертности тела является величина, называемая массой.
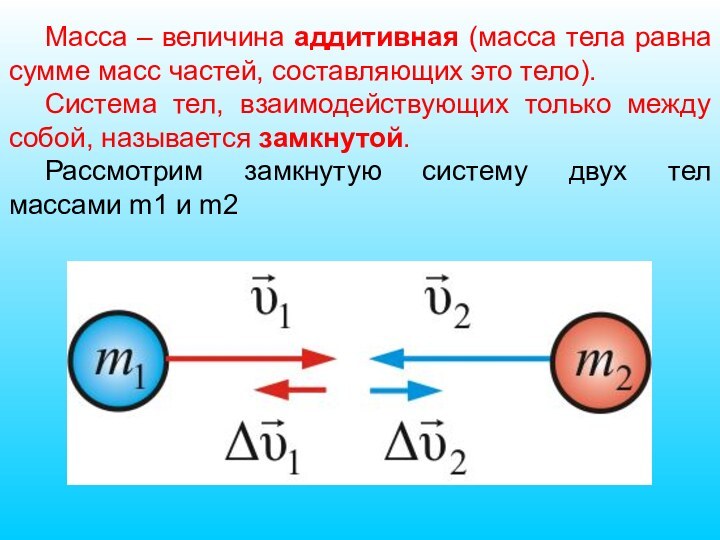
Слайд 9 Масса – величина аддитивная (масса тела равна сумме
масс частей, составляющих это тело).
Система тел, взаимодействующих только между
собой, называется замкнутой.Рассмотрим замкнутую систему двух тел массами m1 и m2
Слайд 10
Приняв во внимание направление скоростей, запишем:
Произведение массы тела
на скорость называется импульсом тела
(тело, обладающее большей массой,
меньше изменяет скорость).
Слайд 11
3. Второй закон Ньютона.
Математическое выражение второго закона
Ньютона:
скорость изменения импульса тела равна действующей на него силе.
Отсюда
можно заключить, что изменение импульса тела равно импульсу силы. т. к.
,
то
но
тогда
Слайд 12
основное
уравнение динамики поступательного движения материальной точки.
Принцип суперпозиции или принцип
независимости действия силЕсли на материальное тело действуют несколько сил, то результирующую силу можно найти из выражения:
Слайд 13 Найдем изменение импульса тела за конечный промежуток времени
изменение импульса тела равно импульсу силы.
Слайд 14 В системе СИ семь основных единиц (м) –
метр,
(кг) – килограмм,
(с) – секунда,
(А) – ампер,
(К)
– кельвин, (кд) – кандела (единица силы света), (кмоль) – единица количества вещества.
Остальные единицы производные
получаются из физических законов связывающих их с основными единицами. Например из второго закона Ньютона производная единица силы
1 кг·м/с2 = 1 Н.
Слайд 15
4. Третий закон Ньютона
Действие тел друг на друга
носит характер взаимодействия.
Третий закон Ньютона отражает тот факт, что
сила есть результат взаимодействия тел, и устанавливает, что силы, с которыми действуют друг на друга два тела, равны по величине и противоположны по направлению.
Слайд 16
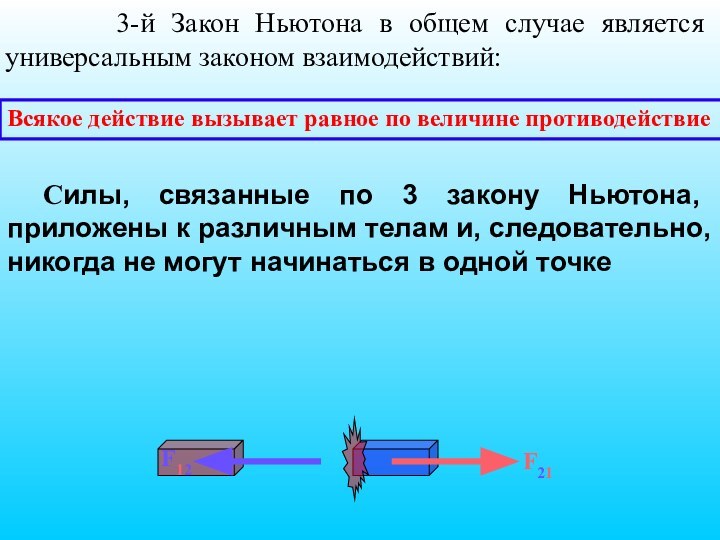
Всякое действие вызывает равное по величине противодействие
3-й Закон Ньютона в общем случае является
универсальным законом взаимодействий:F21
F12
Cилы, связанные по 3 закону Ньютона, приложены к различным телам и, следовательно, никогда не могут начинаться в одной точке
Слайд 18
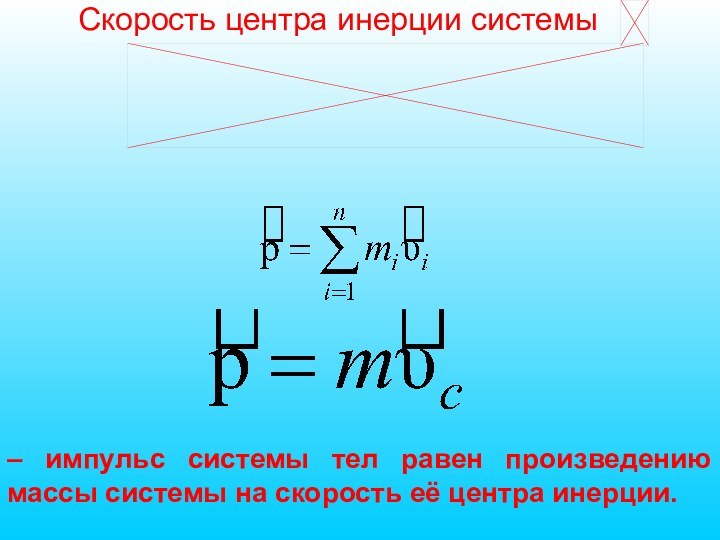
– импульс системы тел равен произведению массы системы
на скорость её центра инерции.
Скорость центра инерции системы
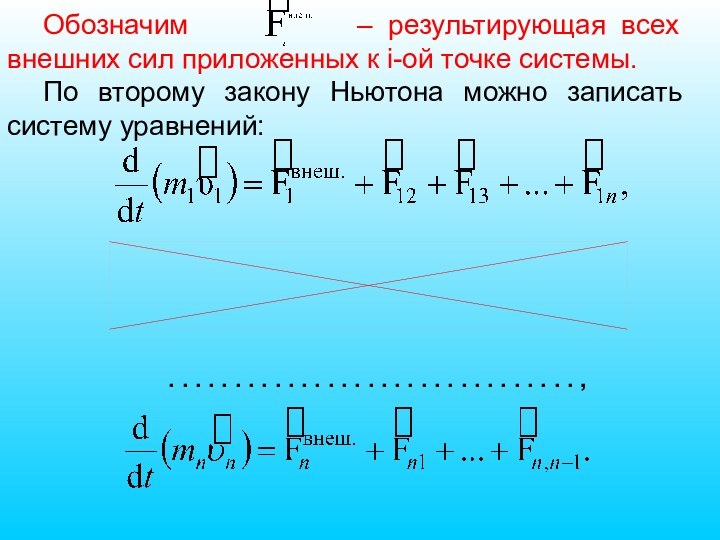
Слайд 20 Обозначим – результирующая
всех внешних сил приложенных к i-ой точке системы.
По второму
закону Ньютона можно записать систему уравнений:. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ,
Слайд 21 Сложим эти уравнения и сгруппируем попарно силы
и
По третьему закону Ньютона,
поэтому все выражения в скобках в правой части уравнения равны нулю. Тогда остаётся:Назовем – главным вектором всех внешних сил,
тогда:
Слайд 22 Скорость изменения импульса системы равна главному вектору всех
внешних сил, действующих на эту систему.
Это уравнение называют основным уравнением динамики поступательного движения системы тел.
Здесь – ускорение центра инерции.
Слайд 23 Центр механической системы движется как материальная точка, масса
которой равна массе всей системы, и на которую действует
сила, равная главному вектору внешних сил, приложенных к системе.
Слайд 24
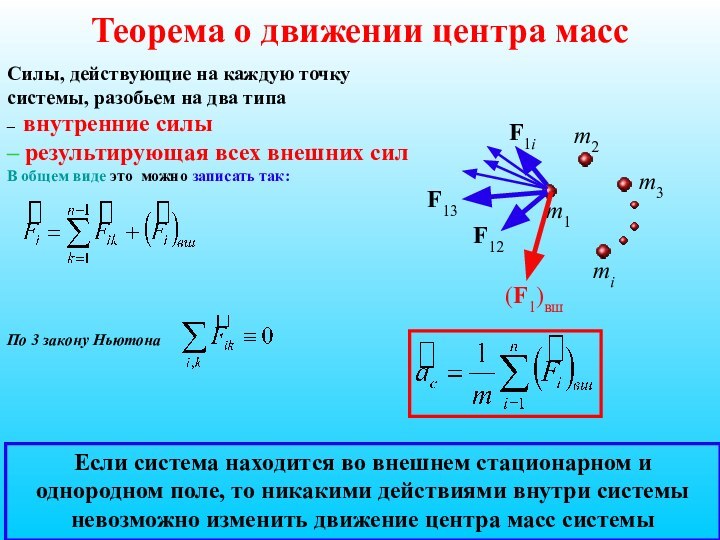
Теорема о движении центра масс
Силы, действующие на каждую
точку системы, разобьем на два типа
– внутренние силы
–
результирующая всех внешних силВ общем виде это можно записать так:
m1
mi
m2
m3
F12
F13
F1i
(F1)вш
По 3 закону Ньютона
Если система находится во внешнем стационарном и однородном поле, то никакими действиями внутри системы невозможно изменить движение центра масс системы
Слайд 26
отсюда
импульс замкнутой системы не изменяется во времени.
Импульс системы
тел может быть представлен в виде произведения суммарной массы
тел на скорость центра инерции: тогда При любых процессах, происходящих в замкнутых системах, скорость центра инерции сохраняется неизменной.
Слайд 28
СИЛЫ В МЕХАНИКЕ
1. Виды и категории сил в
природе
2. Сила тяжести и вес тела
3. Упругие силы
4. Силы
трения5. Силы инерции
5.1. Уравнения Ньютона для неинерциальной системы отсчета
5.2. Центростремительная и центробежная силы
5.3. Сила Кориолиса
Слайд 29
1. Виды и категории сил в природе
В настоящее
время, различают четыре типа сил или взаимодействий:
гравитационные;
электромагнитные; сильные (ответственное за связь частиц в ядрах) и
слабые (ответственное за распад частиц)
Слайд 30 Гравитационные и электромагнитные силы нельзя свести к другим,
более простым силам, поэтому их называют фундаментальными.
где r –
расстояние между точками
Слайд 32
2. Сила тяжести и вес тела
Силы тяжести –
сила, с которой все тела притягиваются к Земле.
Вблизи поверхности
Земли все тела падают с одинаковым ускорением – ускорением свободного падения g
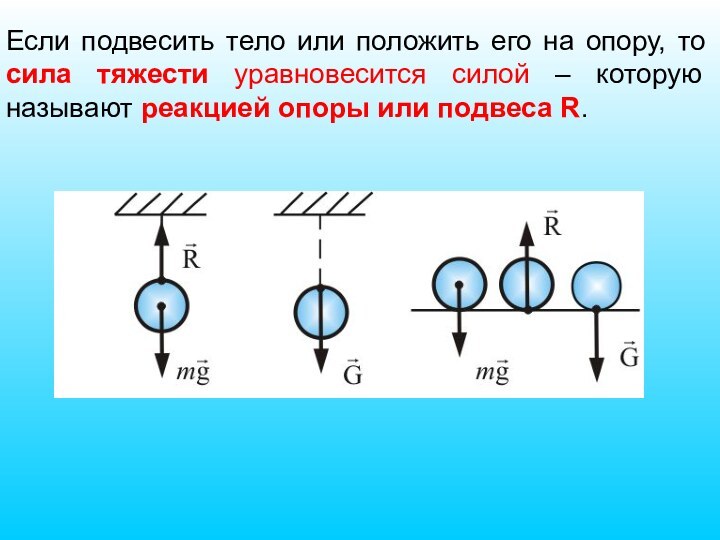
Слайд 33 Если подвесить тело или положить его на опору,
то сила тяжести уравновесится силой – которую называют реакцией
опоры или подвеса R.
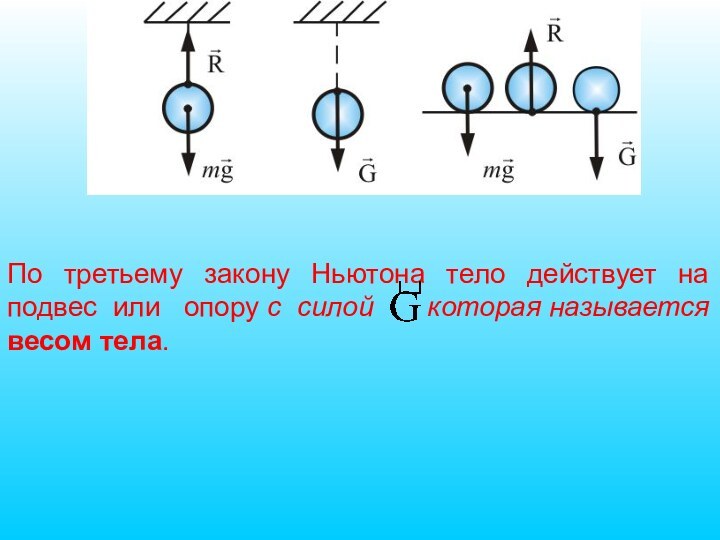
Слайд 34
По третьему закону Ньютона тело действует на подвес
или опору с силой которая
называется весом тела.
Слайд 35 Вес и сила тяжести равны друг другу, но
приложены к разным точкам: вес к подвесу или опоре,
сила тяжести – к самому телу.Это равенство справедливо, если подвес (опора) и тело покоятся относительно Земли (или двигаются равномерно, прямолинейно). Если имеет место движение с ускорением, то справедливо соотношение:
Слайд 36
Вес тела может быть больше или меньше силы
тяжести:
Находясь внутри закрытой кабины невозможно определить, чем вызвана сила
mg, тем, что кабина движется с ускорением или действием притяжения Земли. Пассажиры космического корабля, вращающегося с частотой всего 9,5 об/мин, находясь на расстоянии 10 м от оси вращения, будут чувствовать себя, как на Земле.
Слайд 37
3. Упругие силы
Электромагнитные силы проявляют себя как упругие
силы и силы трения.
Под действием внешних сил возникают деформации
(т.е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой.
Слайд 38
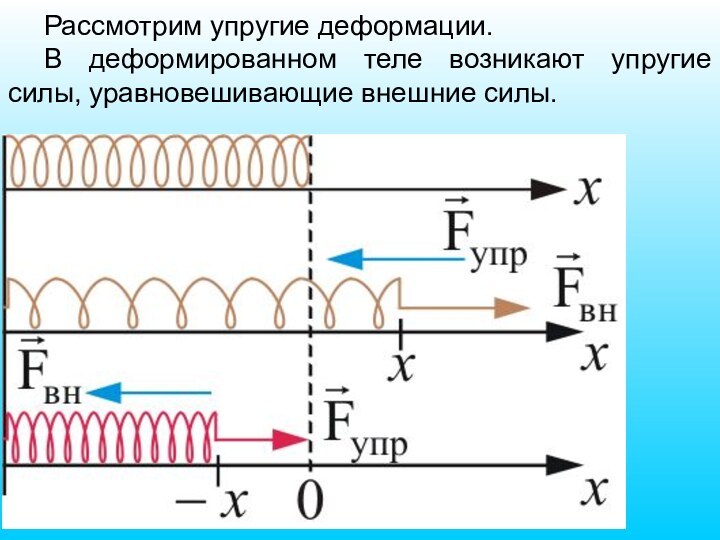
Рассмотрим упругие деформации.
В деформированном теле возникают упругие силы,
уравновешивающие внешние силы.
Слайд 39 Упругие силы возникают во всей деформированной пружине. Любая
часть пружины действует на другую часть с силой упругости
Fупр. Под действием внешней силы – Fвн. пружина получает удлинение x, в результате в ней возни-кает упругая сила – Fупр, уравновешивающая Fвн.
Удлинение пружины пропорционально внешней силе и определяется законом Гука:
k – жесткость пружины.
Слайд 40 Так как упругая сила отличается от внешней только
знаком, т.е.
то закон Гука можно записать в виде:
Слайд 41
Тогда полная работа, которая совершена пружиной, равна:
Потенциальная
энергия упругой пружины равна работе, совершенной над пружиной.
Так как
сила не постоянна, то элементарная работа равна
Слайд 42
4. Силы трения
Трение подразделяется на внешнее и внутреннее.
Внешнее
трение возникает при относительном перемещении двух соприкасающихся твердых тел
(трение скольжения или трение покоя).Внутреннее трение наблюдается при относительном перемещении частей одного и того же сплошного тела (например, жидкость или газ).
Различают сухое и жидкое (или вязкое) трение.
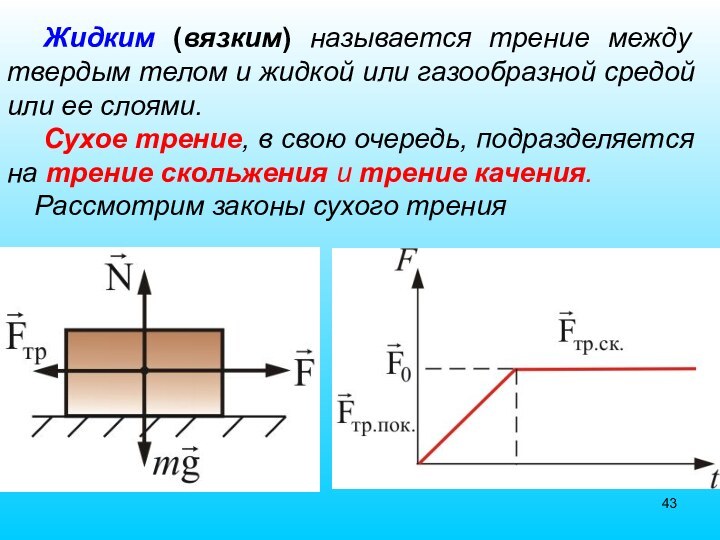
Слайд 43 Жидким (вязким) называется трение между твердым телом и
жидкой или газообразной средой или ее слоями.
Сухое трение, в
свою очередь, подразделяется на трение скольжения и трение качения.Рассмотрим законы сухого трения
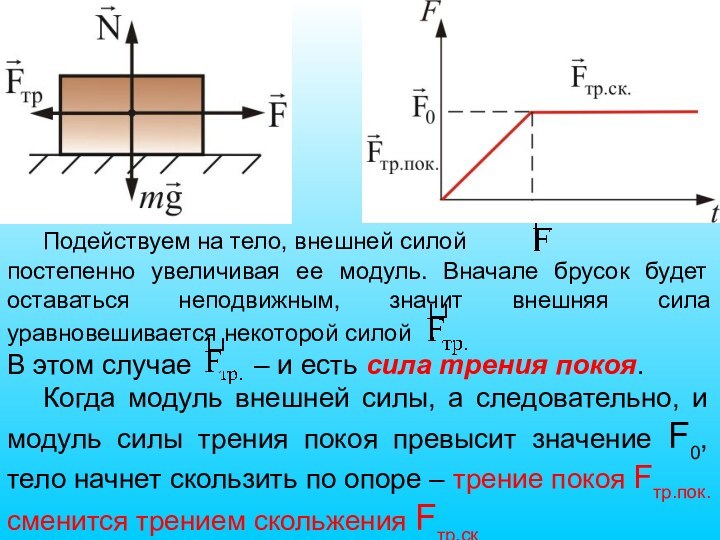
Слайд 44 Подействуем на тело, внешней силой
постепенно увеличивая ее модуль. Вначале брусок будет оставаться неподвижным,
значит внешняя сила уравновешивается некоторой силой В этом случае – и есть сила трения покоя.
Когда модуль внешней силы, а следовательно, и модуль силы трения покоя превысит значение F0, тело начнет скользить по опоре – трение покоя Fтр.пок. сменится трением скольжения Fтр.ск
Слайд 45 Установлено, что максимальная сила трения покоя не зависит
от площади соприкосновения тел и приблизительно пропорциональна модулю силы
нормального давления Nμ0 – коэффициент трения покоя – зависит от природы и состояния трущихся поверхностей.
Аналогично и для силы трения скольжения:
Слайд 46 5. Силы инерции 5.1. Уравнение Ньютона для неинерциальных систем
отсчета
Законы инерции выполняются в инерциальной системе отсчета.
А как
описать движение тела в неинерциальной системе?Пример: вы стоите в троллейбусе спокойно. Вдруг троллейбус резко трогается, и вы невольно отклонитесь назад. Что произошло? Кто вас толкнул?
Слайд 47 С точки зрения наблюдателя на Земле (в инерциальной
системе отсчета), в тот момент, когда троллейбус тронулся, вы
остались стоять на месте – в соответствии с первым законом Ньютона.С точки зрения сидящего в троллейбусе – вы начали двигаться назад, как если бы кто-нибудь вас толкнул. На самом деле, никто не толкнул, просто ваши ноги, связанные силами трения с троллейбусом «поехали» вперед из-под вас и вам пришлось падать назад.
Можно описать ваше движение в инерционной системе отсчета. Но это не всегда просто, так как обязательно нужно вводить силы, действующие со стороны связей.
Слайд 49 Силы, действующие со стороны связей могут быть
самыми разными и ведут себя по разному – нет
единого подхода к их описанию. Силы инерции обусловлены не взаимодействием тел, а свойствами самих неинерциальных систем отсчета.На силы инерции законы Ньютона не распространяются.
Можно в неинерциальной системе воспользоваться законами Ньютона, если ввести силы инерции.
Силы инерции вводят специально, чтобы воспользоваться уравнениями Ньютона в неинерциальной системе.
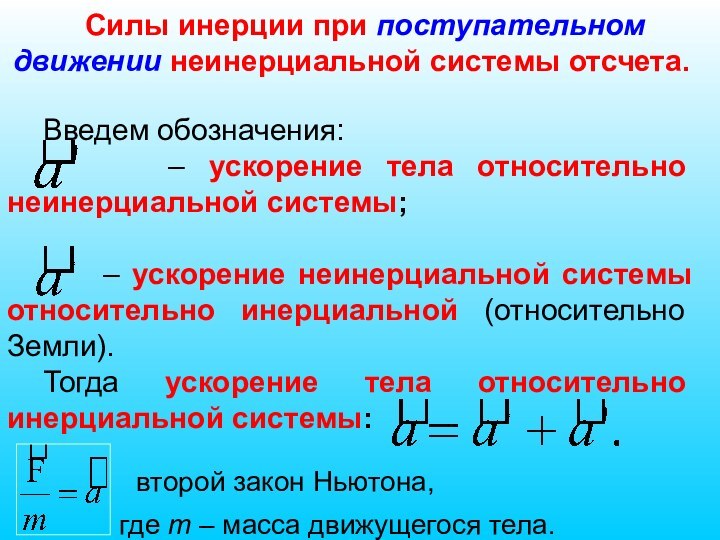
Слайд 50
Силы инерции при поступательном движении неинерциальной системы отсчета.
Введем
обозначения:
– ускорение тела относительно неинерциальной системы;
– ускорение неинерциальной системы относительно инерциальной (относительно Земли).
Тогда ускорение тела относительно инерциальной системы:
второй закон Ньютона,
где m – масса движущегося тела.
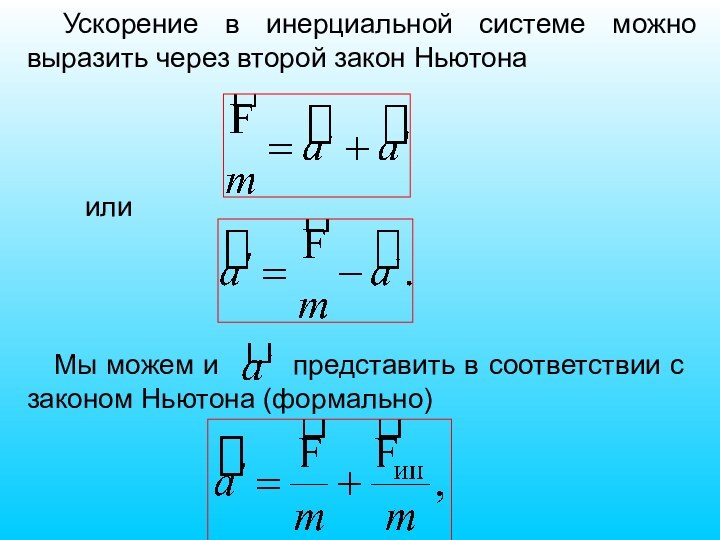
Слайд 51 Ускорение в инерциальной системе можно выразить через второй
закон Ньютона
или
Мы можем и представить в
соответствии с законом Ньютона (формально)
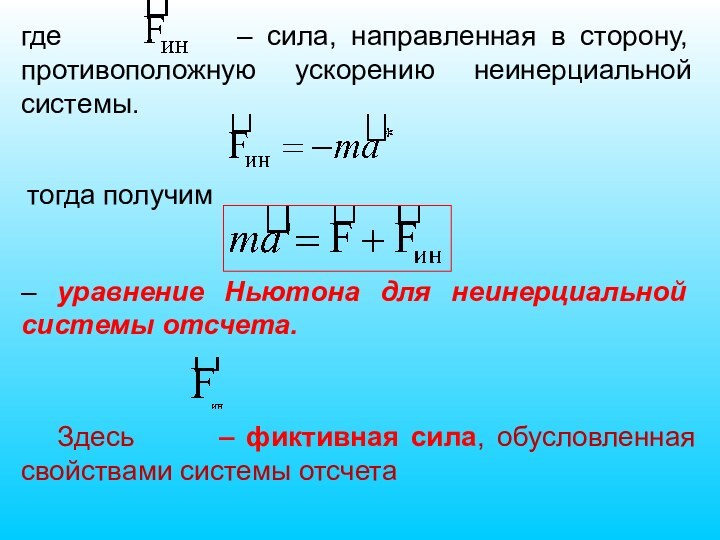
Слайд 52 где – сила,
направленная в сторону, противоположную ускорению неинерциальной системы.
тогда получим
–
уравнение Ньютона для неинерциальной системы отсчета. Здесь – фиктивная сила, обусловленная свойствами системы отсчета
Слайд 53 Силы инерции неинвариантны относительно перехода из одной системы
отсчета в другую. Они не подчиняются закону действия и
противодействия. Движения тела под действием сил инерции аналогично движению во внешнем силовом поле.Силы инерции всегда являются внешним по отношению к любому движению системы материальных тел.
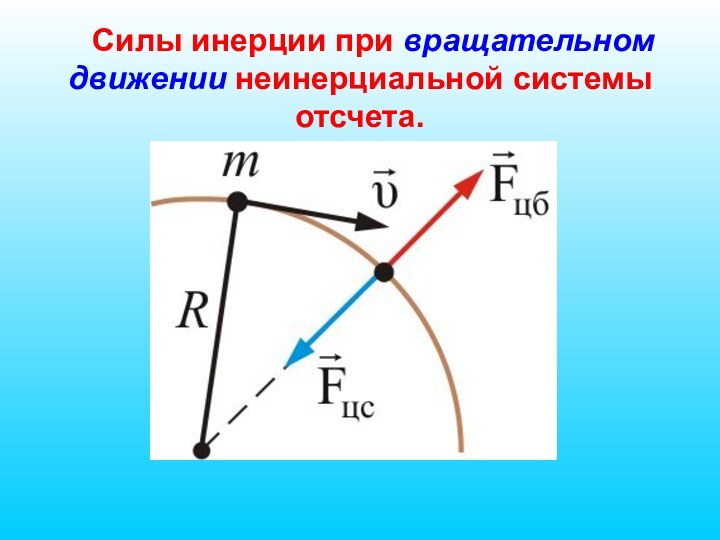
Слайд 55
5.2. Центростремительная и центробежная силы
В каждый момент времени
камень должен был бы двигаться прямолинейно по касательной к
окружности. Однако он связан с осью вращения веревкой. Веревка растягивается, появляется упругая сила, действующая на камень, направленная вдоль веревки к центру вращения.Это и есть центростремительная сила (при вращении Земли вокруг оси в качестве центростремительной силы выступает сила гравитации).
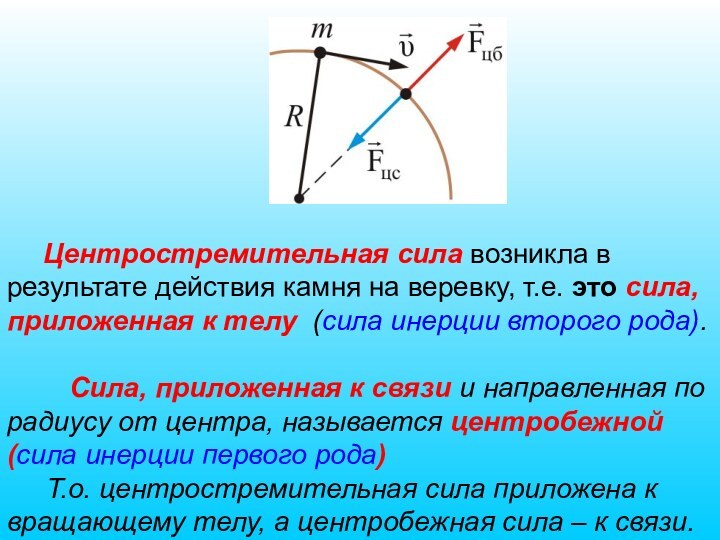
Слайд 57 Центростремительная сила возникла в результате действия
камня на веревку, т.е. это сила, приложенная к телу
(сила инерции второго рода).Сила, приложенная к связи и направленная по радиусу от центра, называется центробежной (сила инерции первого рода)
Т.о. центростремительная сила приложена к вращающему телу, а центробежная сила – к связи.
Слайд 59
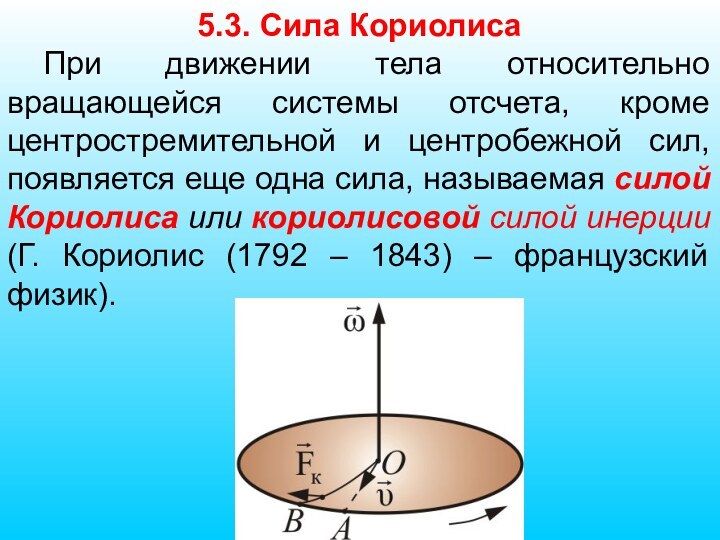
5.3. Сила Кориолиса
При движении тела относительно вращающейся
системы отсчета, кроме центростремительной и центробежной сил, появляется еще
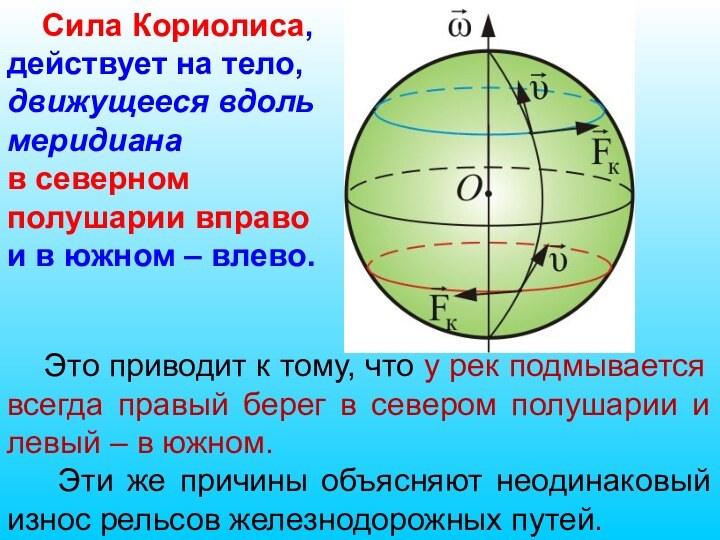
одна сила, называемая силой Кориолиса или кориолисовой силой инерции (Г. Кориолис (1792 – 1843) – французский физик).Слайд 60 Это приводит к тому, что у
рек подмывается всегда правый берег в севером полушарии и
левый – в южном.Эти же причины объясняют неодинаковый износ рельсов железнодорожных путей.
Сила Кориолиса, действует на тело, движущееся вдоль меридиана
в северном полушарии вправо
и в южном – влево.





























