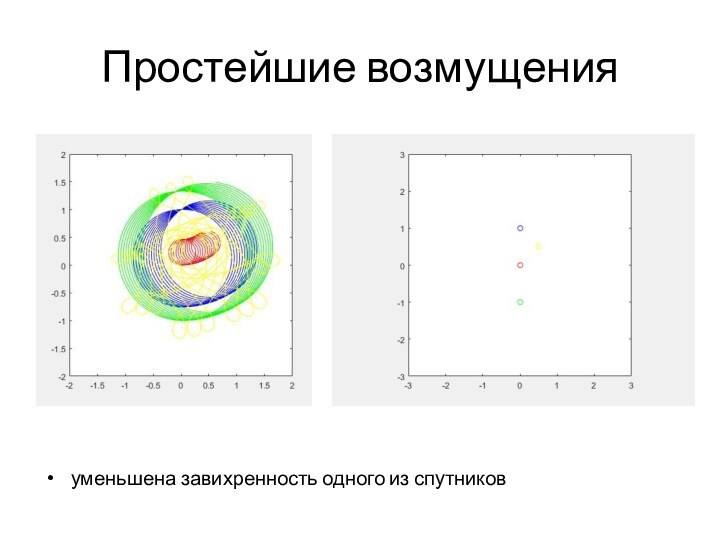
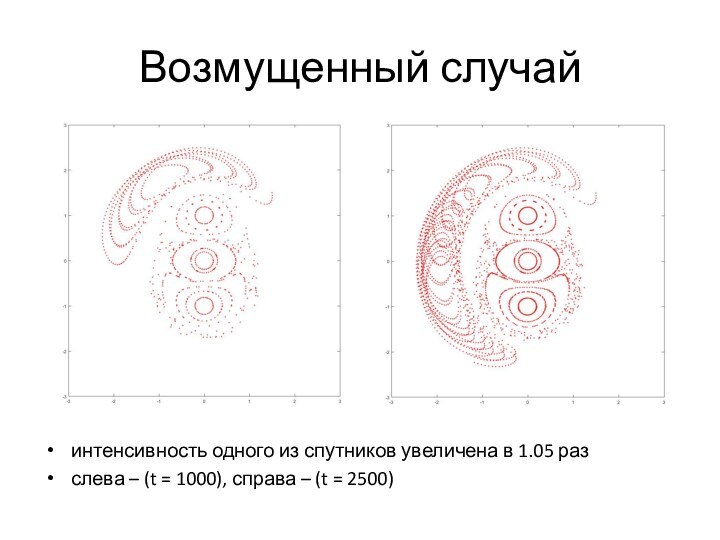
y) - координаты пассивной частицы
wi – завихренность i-го вихря
Ψ
– функция тока
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Динамика жидких частиц в поле скорости точечного триполя
Содержание
- 2. Постановка задачи(xi, yi) – координаты i-го вихря,
- 3. Невозмущенное состояниепассивная частица не выходит из окрестности одного из вихрей
- 4. Невозмущенное состояниепассивная частица циркулирует в триполе, не выходя за определенные границы
- 5. Устойчивостьдвижение пассивной частицы структурно устойчиво
- 6. Простейшие возмущенияувеличена завихренность одного из спутников
- 7. Простейшие возмущенияуменьшена завихренность одного из спутников
- 8. Устойчивостьдинамика пассивной частицы становится структурно неустойчивой
- 9. Сечения Пуанкареx – начальное положение точки (пассивной частицы)P(x) – отображение Пуанкаре точки xx* - неподвижная точка
- 10. Невозмущенный случайСечение Пуанкаре плоскостью x0 = x1x0 - абсцисса центрального вихряx1 - абсцисса одного из спутников
- 11. Возмущенный случайинтенсивность одного из спутников увеличена в
- 12. Скачать презентацию
- 13. Похожие презентации
Постановка задачи(xi, yi) – координаты i-го вихря, (x, y) - координаты пассивной частицыwi – завихренность i-го вихряΨ – функция тока
Слайд 2
Постановка задачи
(xi, yi) – координаты i-го вихря, (x,
y) - координаты пассивной частицы
– функция тока
Слайд 4
Невозмущенное состояние
пассивная частица циркулирует в триполе, не выходя
за определенные границы
Слайд 9
Сечения Пуанкаре
x – начальное положение точки (пассивной частицы)
P(x)
– отображение Пуанкаре точки x
x* - неподвижная точка
Слайд 10
Невозмущенный случай
Сечение Пуанкаре плоскостью x0 = x1
x0 -
абсцисса центрального вихря
x1 - абсцисса одного из спутников
Слайд 11
Возмущенный случай
интенсивность одного из спутников увеличена в 1.05
