- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ЭДС при несинусоидальном токе
Содержание
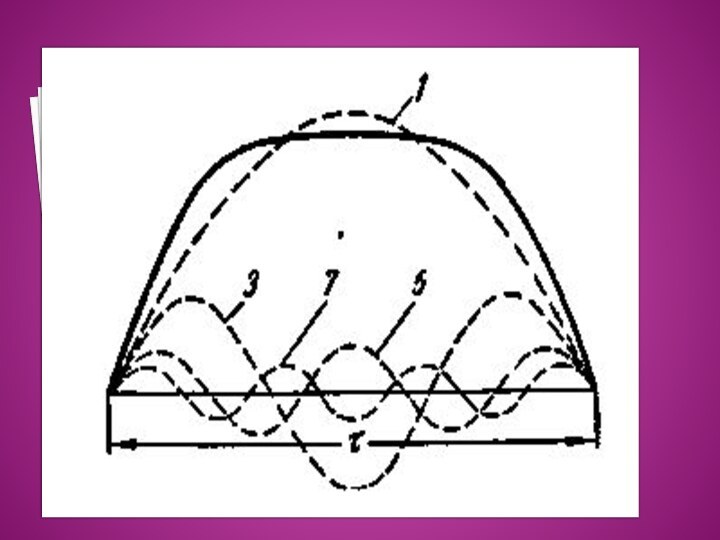
Электродвижущие силы при несинусоидальном поле. На рисунке представлена кривая поля (сплошная линия), созданного, например, вращающимися полюсами. Ее можно разложить на гармоники, причем вследствие симметрии кривой относительно оси абсцисс и максимальной ординаты в разложении будут иметь







Слайд 3
Электродвижущие силы при несинусоидальном поле.
На рисунке представлена
кривая поля (сплошная линия), созданного, например, вращающимися полюсами.
можно разложить на гармоники, причем вследствие симметрии кривой относительно оси абсцисс и максимальной ординаты в разложении будут иметь место только синусоиды нечетного порядка, показанные на пунктиром. Все гармоники поля вращаются относительно статора с одной и той же частотой, равной частоте вращения полюсов. Полюсное деление первой или основной гармоники равно τ, полюсное деление ν-й гармоники равно τ / ν. Таким образом, ν -я гармоника поля имеет в ν раз больше полюсов, чем первая гармоника.
Слайд 4
Электродвижущая сила, наведенная
в фазе обмотки ν -й гармоникой поля, равна:
E ν=4,44f
νwk0 νФm ν,Где f ν = ν pn/60= ν f1 –частота ν -й гармоники ЭДС в ν раз большая, чем частота f1 первой гармоники э.д.с.;
Фм ν =(2/π ) (τ/ν)l В m ν - поток, соответствующий ν -й гармонике поля
k0 ν= ky ν kpν — обмоточный коэффициент для ν -й гармоники э.д.с.
Слайд 5
Обмоточный коэффициент k01 для первой гармоники, очевидно,
не отличается от k0, рассмотренного нами ранее; k0 ν
для высших гармоник отличается от k01, так как сдвиг по фазе э.д.с. сторон витка и э.д.с. катушек, составляющих катушечную группу, зависит от номера гармоники ν.Сдвиг по фазе э.д.с. сторон витка, наведенных ν -й гармоникой поля, равен
νγ, где γ — сдвиг сторон витка в электрических градусах для первой гармоники поля; следовательно, ky ν= sin νγ/2= sin ν (y/τ) 900
Слайд 6
Коэффициент распределения для ν-й гармоники рассчитывается по
формуле
kpν =(sin νqα/2)/(qsin(να/2)),
Таким образом путем выбора шага мы
можем значительно уменьшить амплитуды высших гармоник в кривой фазной э.д.с.Действующее значение фазной э.д.с.
E=√E12 + E32+E52 +…
Так как в обычных случаях амплитуды высших гармоник сравнительно с амплитудой первой гармоники невелики, мы можем практически считать:
E ν=Е1=4,44f νwk0 1Ф
Слайд 7
где f1 и k01 определяются
для первой гармоники, а Ф (индекс «м» здесь и
в последующем опускаем) — по первой гармонике кривой поля (или приближенно по действительной кривой поля).Гармоники фазных э.д.с. трехфазной обмотки с номером, кратным трем, совпадают по фазе, прочие гармоники фазных э.д.с. (5, 7, 11, 13. 17, ...) той же обмотки будут сдвинуты по фазе на 120°.
Следовательно, при соединении обмотки звездой в линейной э.д.с. все гармоники с номером, кратным трем, пропадают:





























