- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Электрические цепи синусоидального тока
Содержание
- 2. Содержание1. Идеальные элементы в цепи синусоидального тока
- 3. Идеальный индуктивный элемент в цепи синусоидального тока.
- 4. Идеальный индуктивный элемент в цепи синусоидального тока
- 5. где величина
- 6. При графическом изображении временными диаграммами
- 7. При аналитическом изображении комплексными числами
- 8. На векторной диаграмме вектор напряжения повернут относительно
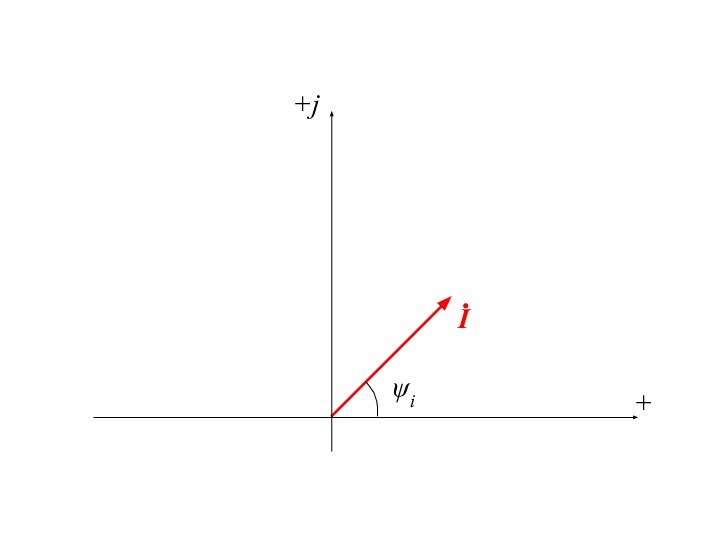
- 9. ψi+j+
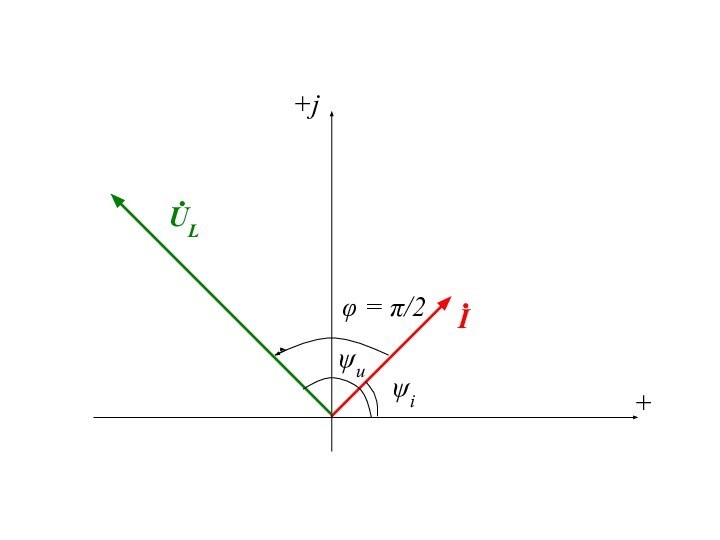
- 10. ψuψiφ = π/2+j+
- 11. Для анализа энергетических соотношений в
- 12. В цепи с идеальным индуктивным элементом мгновенная
- 13. В индуктивном элементе происходит непрерывный колебательный процесс
- 14. Необходимо определить соотношение между синусоидальными
- 15. • ток в емкостном элементе изменяется по синусоидальному
- 16. где величина
- 17. При графическом изображении временными диаграммами
- 18. При аналитическом изображении комплексными числами
- 19. На векторной диаграмме вектор напряжения повернут относительно
- 20. ψi+j+
- 21. ψiψuφ = - π/2+j+
- 22. Для анализа энергетических соотношений в
- 23. В цепи с идеальным индуктивным элементом мгновенная
- 24. В емкостном элементе происходит непрерывный колебательный процесс
- 25. Заключение1.На идеальном индуктивном элементе соотношение между током
- 26. Заключение2.На идеальном емкостном элементе соотношение между током
- 27. Контрольные вопросыПоставить в соответствие векторную диаграмму и схему замещения
- 28. Контрольные вопросыОпределить ток и реактивную индуктивную мощность
- 29. Скачать презентацию
- 30. Похожие презентации


























Слайд 2
Содержание
1. Идеальные элементы в цепи синусоидального тока (продолжение)
Идеальный
индуктивный элемент в цепи синусоидального тока.
цепи синусоидального тока.
Слайд 3
Идеальный индуктивный элемент в цепи синусоидального тока.
Необходимо определить соотношение между синусоидальными током и напряжением по
величине и по фазе.i = Im sin (ωt+ψi)
Синусоидальный ток создает переменное магнитное поле, которое, наводит в индуктивном элементе ЭДС самоиндукции.
На основании второго закона Кирхгофа для рассматриваемой цепи можно записать:
Слайд 4
Идеальный индуктивный элемент в цепи синусоидального тока (продолжение).
или
• напряжение
на индуктивном элементе изменяется по синусоидальному закону с амплитудой
и действующим значением
• начальная фаза напряжения больше начальной фазы тока на π/2, при этом разность фаз, определяемая выражением
Напряжение на индуктивном элементе
опережает ток по фазе на угол φ = π/2.
Слайд 5 где величина
называется индуктивным сопротивлением.
Единица индуктивного сопротивления – Ом.
Соотношение по величине между током и напряжением индуктивного элемента определяется законом Ома : действующее значение тока индуктивного элемента прямо пропорционально действующему значению напряжения и обратно пропорционально индуктивному сопротивлению.
Идеальный индуктивный элемент в цепи синусоидального тока (продолжение).
Слайд 6 При графическом изображении временными диаграммами синусоида
напряжения uL(t) сдвинута относительно синусоиды тока i(t) в сторону
опережения на угол φ = π/2. На рисунке показаны временные диаграммы тока и напряжения при начальной фазе тока, равной нулю (ψi = 0). Графики изменения во времени мгновенных значений uL, i, рL
Идеальный индуктивный элемент в цепи синусоидального тока (продолжение).
Слайд 7 При аналитическом изображении комплексными числами с
учетом действующих значений комплексное напряжение имеет вид:
Комплексный ток:
Закон Ома в комплексной форме: Здесь - комплексное индуктивное
сопротивление.
Идеальный индуктивный элемент в цепи синусоидального тока (продолжение).
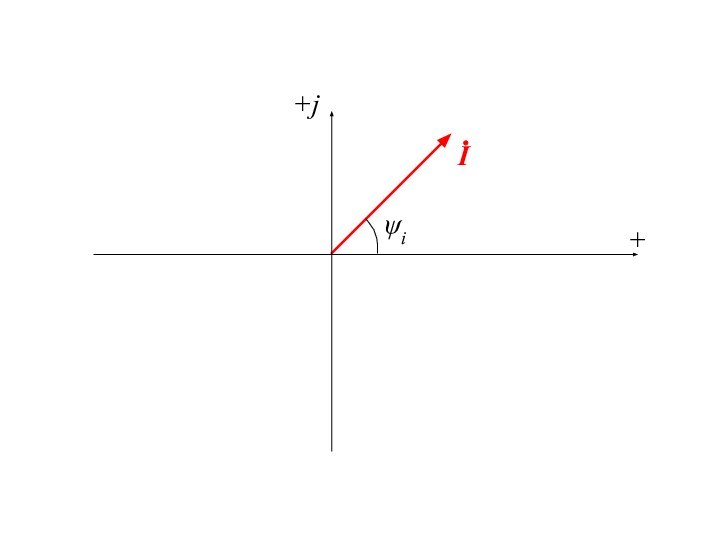
Слайд 8 На векторной диаграмме вектор напряжения повернут относительно вектора
тока на угол π/2 в сторону опережения (против часовой
стрелки)При изменении начальной фазы напряжения оба вектора повернутся на соответствующий угол. Однако взаимное относительное направление векторов не меняется.
Это отражает свойства идеального индуктивного элемента
Идеальный индуктивный элемент в цепи синусоидального тока (продолжение).
Подробней
Слайд 11 Для анализа энергетических соотношений в цепи
с идеальным индуктивным элементом определим характер мощности в этой
цепи.Примем начальную фазу тока, равной нулю (ψi = 0). При этом начальная фаза напряжения ψu = π/2. Мгновенная мощность в индуктивном элементе:
Перейдя к действующим значениям напряжения и тока
и
Полученное выражение описывает характер изменения мощности в идеальном индуктивном элементе..
Идеальный индуктивный элемент в цепи синусоидального тока (продолжение).
Слайд 12 В цепи с идеальным индуктивным элементом мгновенная мощность
изменяется по синусоидальному закону с амплитудой UL·I с двойной
частотой 2ω .В течение периода значение мгновенной мощности меняет знак через каждую четверть периода. При рL > 0 – электрическая энергия от источника поступает в цепь и преобразуется в энергию магнитного поля в индуктивном элементе. При рL < 0 – энергия, запасенная в магнитном поле, полностью возвращается к источнику.
Среднее за период значение мгновенной мощности или активная мощность равна нулю:
Идеальный индуктивный элемент в цепи синусоидального тока (продолжение).
Слайд 13 В индуктивном элементе происходит непрерывный колебательный процесс обмена
энергией между источником и магнитным полем индуктивного приемника. Это
обратимый процесс преобразования энергии.Для характеристики интенсивности этого процесса используют понятие реактивной индуктивной мощности QL. Ее величину определяют амплитудой колебания мгновенной мощности pLmax.
или
Индуктивное сопротивление
Единицы реактивной индуктивной мощности QL –
ВАр, КВАр, МВАр.
Идеальный индуктивный элемент в цепи синусоидального тока (продолжение).
Слайд 14 Необходимо определить соотношение между синусоидальными током
и напряжением по величине и по фазе.
По второму закону
Кирхгофа длязаданной цепи:
Идеальный емкостный элемент в цепи синусоидального тока .
Слайд 15 • ток в емкостном элементе изменяется по синусоидальному закону
с амплитудой
и действующим значением
• начальная фаза тока больше начальной фазы напряжения на π/2, при этом разность фаз, определяемая выражением
Напряжение на емкостном элементе отстает от тока по фазе на угол π/2.
Идеальный емкостный элемент в цепи синусоидального тока (продолжение).
Слайд 16 где величина
называется емкостным сопротивлением.
Единица индуктивного сопротивления – Ом.
Соотношение по величине между током и напряжением индуктивного элемента определяется законом Ома : действующее значение тока емкостного элемента прямо пропорционально действующему значению напряжения и обратно пропорционально емкостному сопротивлению.
Идеальный емкостный элемент в цепи синусоидального тока (продолжение).
Слайд 17 При графическом изображении временными диаграммами синусоида
напряжения uс(t) сдвинута относительно синусоиды тока i(t) в сторону
отставания на угол π/2. На рисунке показаны временные диаграммы тока и напряжения при начальной фазе тока, равной нулю (ψu = 0). Графики изменения во времени мгновенных значений uC,, i, рC.
Идеальный емкостный элемент в цепи синусоидального тока (продолжение).
Слайд 18 При аналитическом изображении комплексными числами с
учетом действующих значений комплексное напряжение имеет вид:
Комплексный ток:
Закон Ома в комплексной форме: Здесь - комплексное индуктивное
сопротивление.
Идеальный емкостный элемент в цепи синусоидального тока (продолжение).
Слайд 19 На векторной диаграмме вектор напряжения повернут относительно вектора
тока на угол π/2 в сторону отставания (по часовой
стрелки)При изменении начальной фазы напряжения оба вектора повернутся на соответствующий угол. Однако взаимное относительное
Это отражает свойства идеального индуктивного элемента .Угол между векторами напряжения и тока на векторной диаграмме определяет разность фаз φ.
Идеальный емкостный элемент в цепи синусоидального тока (продолжение).
Подробней
Слайд 22 Для анализа энергетических соотношений в цепи
с с идеальным емкостным элементом определим характер мощности в
этой цепи.Примем начальную фазу напряжения, равной нулю (ψu = 0). При этом начальная фаза тока ψi = π/2. Мгновенная мощность в индуктивном элементе:
Перейдя к действующим значениям напряжения и тока
и
Полученное выражение описывает характер изменения мощности в идеальном емкостном элементе.
Идеальный емкостный элемент в цепи синусоидального тока (продолжение).
Слайд 23 В цепи с идеальным индуктивным элементом мгновенная мощность
изменяется по синусоидальному закону с амплитудой UС ·I с
двойной частотой 2ω .В течение периода значение мгновенной мощности меняет знак через каждую четверть периода. При рC > 0 – электрическая энергия от источника поступает в цепь и преобразуется в энергию электрического поля в емкостном элементе. При рC < 0 – энергия, запасенная в электрическом поле, полностью возвращается к источнику.
Среднее за период значение мгновенной мощности или активная мощность равна нулю:
Идеальный емкостный элемент в цепи синусоидального тока (продолжение).
Слайд 24 В емкостном элементе происходит непрерывный колебательный процесс обмена
энергией между источником и электрическим полем емкостного приемника. Это
обратимый процесс преобразования энергии.Для характеристики интенсивности этого процесса используют понятие реактивной емкостной мощности QC. Ее величину определяют амплитудой колебания мгновенной мощности pCmax.
или
Емкостное сопротивление
Единицы реактивной емкостной мощности QC –
ВАр, КВАр, МВАр.
Идеальный емкостный элемент в цепи синусоидального тока (продолжение).
Слайд 25
Заключение
1.
На идеальном индуктивном элементе соотношение между током и
напряжением по величине:
Индуктивное сопротивление
Разность фаз в индуктивном
элементеСоотношение комплексных тока и напряжения на идеальном индуктивном элементе
Комплексное индуктивное сопротивление
На векторной диаграмме вектор напряжения повернут относительно вектора тока против часовой стрелки на π/2.
Реактивная индуктивная мощность
Слайд 26
Заключение
2.
На идеальном емкостном элементе соотношение между током и
напряжением по величине:
Емкостное сопротивление
Разность фаз в емкостном
элементеСоотношение комплексных тока и напряжения на идеальном емкостном элементе
Комплексное емкостное сопротивление
На векторной диаграмме вектор напряжения повернут относительно вектора тока по часовой стрелке на π/2.
Реактивная емкостная мощность