- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
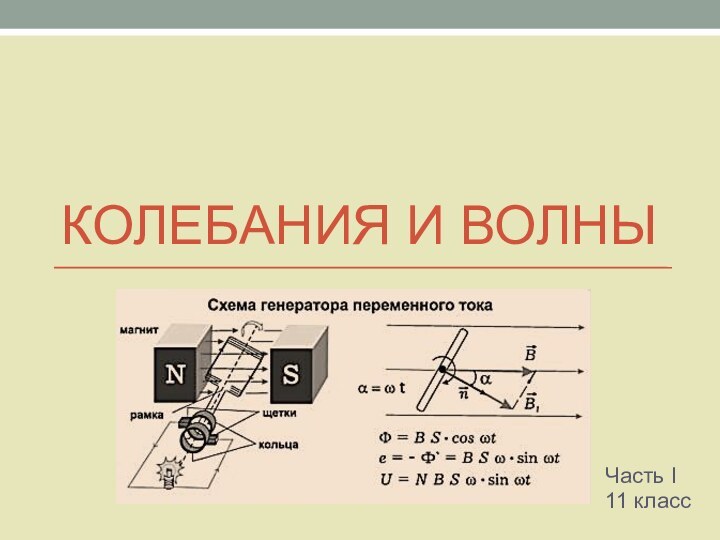
Презентация на тему Колебания и волны
Содержание
- 2. Колебаниями называются процессы различной природы, которые точно или почти точно повторяются через определенные промежутки времени..
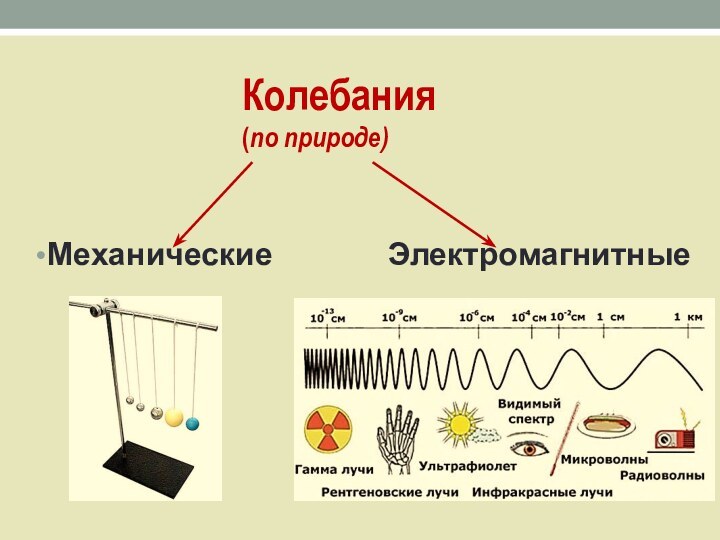
- 3. Колебания (по природе)Механические Электромагнитные
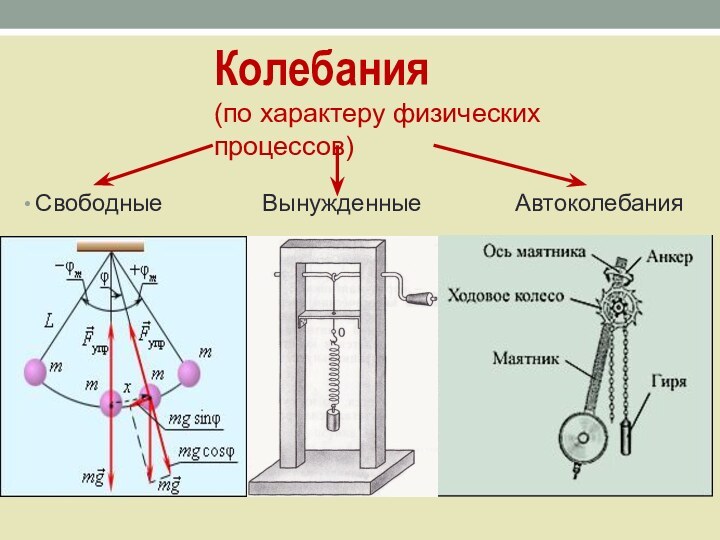
- 4. Колебания (по характеру физических процессов)Свободные
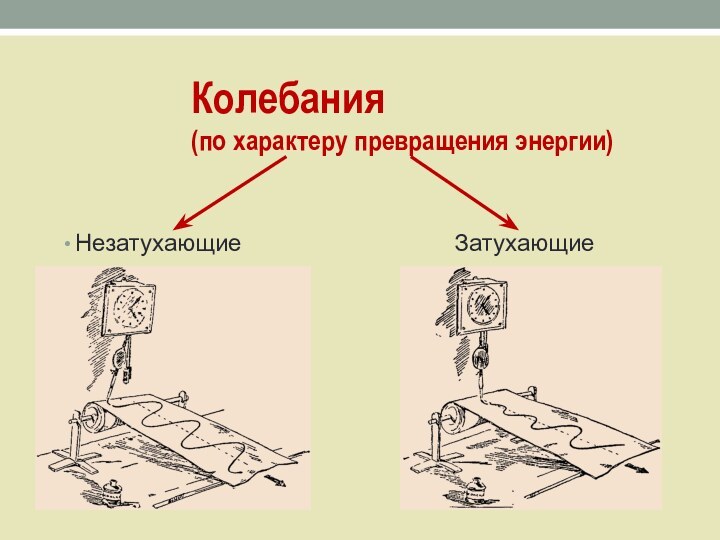
- 5. Колебания (по характеру превращения энергии)Незатухающие
- 6. Колебательная система включает в себя все тела,
- 7. Колебательная система (КС) – система, имеющая положение устойчивого равновесия.Положение устойчивого равновесия:струна
- 8. Свободные колебания – самый простой вид колебаний.Свободные
- 9. Основные характеристики (параметры) колебаний:
- 10. Основные характеристики (параметры) колебаний:
- 11. Х0 Х0
- 12. ХY 123 (нормальное) центростремительное ускорение(тангенциальное) касательное ускорение
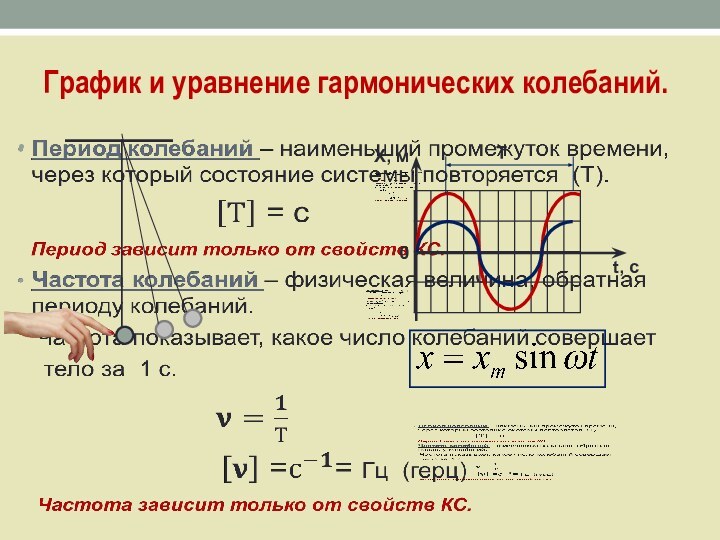
- 13. График и уравнение гармонических колебаний. Х, мt, c0 Т
- 14. Графики и уравнения гармонических колебанийНачало колебаний из
- 15. Уравнения гармонических колебаний.
- 16. Проверим знания!
- 17. Начертите таблицу ответов. В верхней строчке таблицы
- 18. 1. За время, равное периоду колебаний, маятник
- 19. 2. Тело за 1 с совершает 100
- 20. 3. За 1 минуту тело совершило 300
- 21. 4. Амплитуда колебаний пружинного маятника зависит от:
- 22. 5. За одно и то же время
- 23. 6. Начальная фаза гармонических колебаний материальной точки
- 24.
- 25. 8. В уравнении гармонического колебания
- 26. 9. Частота колебаний математического маятника равна:А.В.С.D.
- 27. 10. Длину нити математического маятника увеличили в
- 28. 11. Период колебаний пружинного маятника равен Т.
- 29. 12. Какое из перечисленных ниже действий позволит
- 30. 13. Для гармонического колебания, изображенного на рисунке,
- 31. 14. Материальная точка совершает колебания
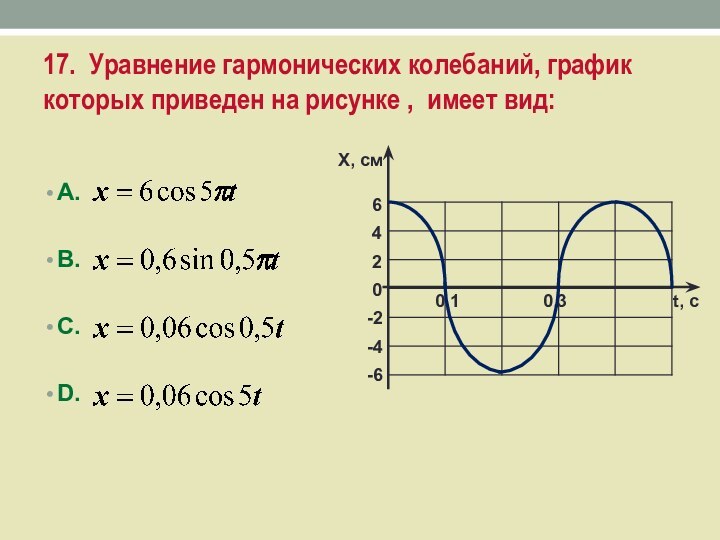
- 32. 15. Уравнение гармонических колебаний материальной точки (график на рисунке) имеет следующий вид:А.B.C.D. Х, м120-1-212345t, c
- 33. 16. Маятниковые часы идут на поверхности Луны
- 34. Скачать презентацию
- 35. Похожие презентации
Колебаниями называются процессы различной природы, которые точно или почти точно повторяются через определенные промежутки времени..






















Слайд 2 Колебаниями называются процессы различной природы, которые точно или
почти точно повторяются через определенные промежутки времени.
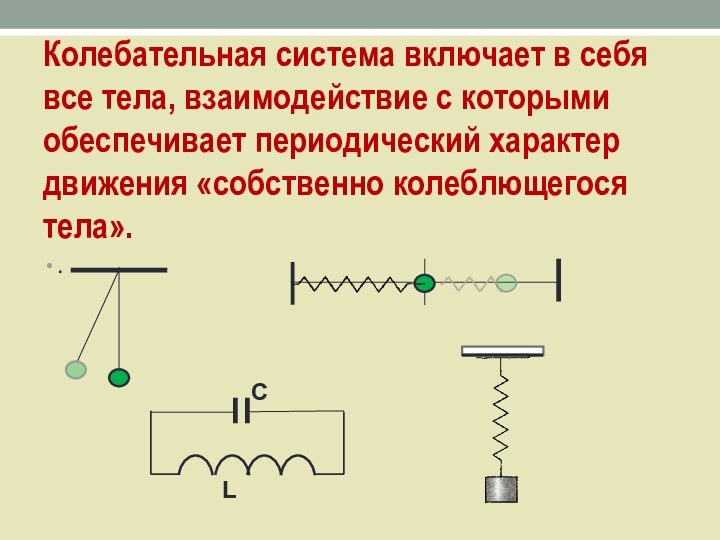
Слайд 6 Колебательная система включает в себя все тела, взаимодействие
с которыми обеспечивает периодический характер движения «собственно колеблющегося тела».
.
С
L
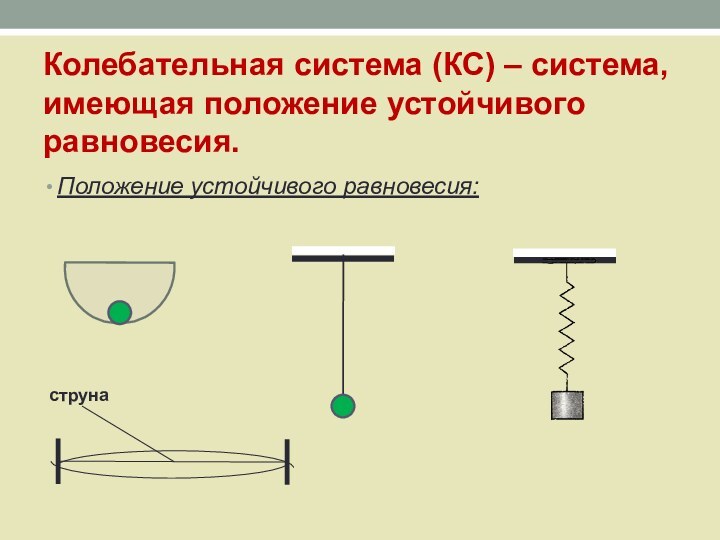
Слайд 7 Колебательная система (КС) – система, имеющая положение устойчивого
равновесия.
Положение устойчивого равновесия:
струна
Слайд 8
Свободные колебания – самый простой вид колебаний.
Свободные колебания
возникают в системе после того, как она была выведена
из состояния равновесия, и происходят под действием внутренних сил, действующих в системе.Свободные колебания могут происходить только в колебательной системе.
Условия необходимые для возникновения в системе свободных колебаний:
1) имеется положение устойчивого равновесия;
2) отсутствие диссипативных сил;
3) выведение системы из состояния равновесия
(сообщение запаса энергии)
Свободные колебания – физическая модель.
Слайд 14
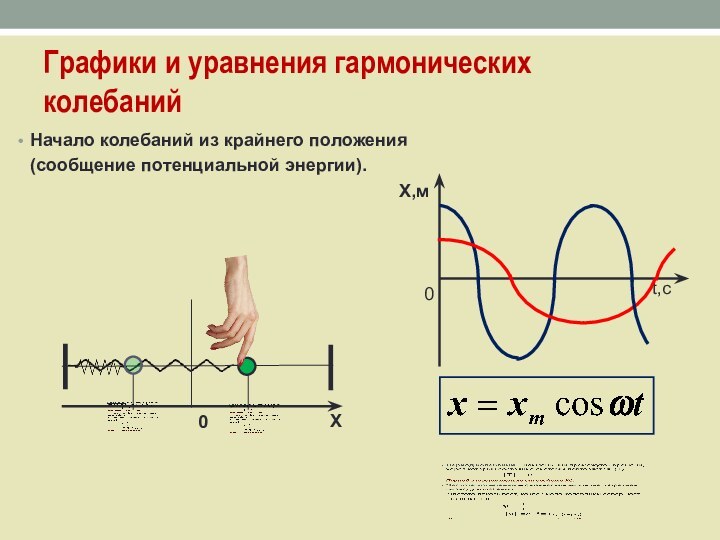
Графики и уравнения гармонических колебаний
Начало колебаний из крайнего
положения
(сообщение потенциальной энергии).
Х,м0
Х
0
t,c
Слайд 17 Начертите таблицу ответов. В верхней строчке таблицы номера вопросов. В
нижнюю строчку таблицы запишите букву, соответствующую правильному, на Ваш
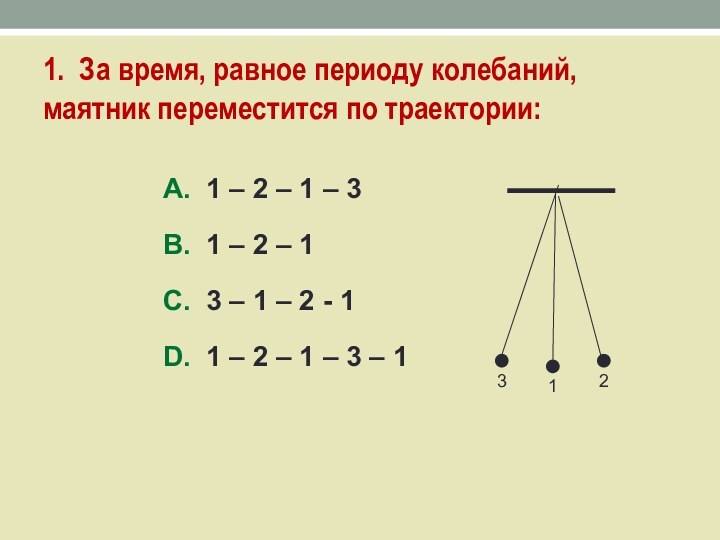
взгляд, ответу.Слайд 18 1. За время, равное периоду колебаний, маятник переместится
по траектории:
A. 1 – 2 – 1 – 3
B.
1 – 2 – 1C. 3 – 1 – 2 - 1
D. 1 – 2 – 1 – 3 – 1
1
2
3
Слайд 19 2. Тело за 1 с совершает 100 колебаний.
Период колебаний равен:
A. 100 с
B. 0,01 с
С. 60
сD. 0,6 c
Слайд 20 3. За 1 минуту тело совершило 300 колебаний.
Частота колебаний равна:
А. 300 Гц
B. 5 Гц
С.
0,2 ГцD. 20 Гц
Слайд 21
4. Амплитуда колебаний пружинного маятника зависит от:
А.
Массы груза
B. Жесткости пружины
C. От первоначального запаса энергии
D. От
массы груза, жесткости пружины и первоначального запаса энергии. Слайд 22 5. За одно и то же время первый
математический маятник совершает одно колебание, а второй – четыре.
Нить первого маятникаА. в 16 раз длиннее
В. в 4 раза длиннее
С. в 2 раза длиннее
D. в 2 раза короче.
Слайд 23
6. Начальная фаза гармонических колебаний материальной точки определяет:
А.
Амплитуду точки
В. Отклонение точки от положения равновесия в начальный
момент времениС. Период и частоту колебаний
D. Максимальную скорость прохождения точкой положения равновесия.
Слайд 25 8. В уравнении гармонического колебания величина, стоящая под
знаком косинуса, называется:
А. Амплитудой
В. Циклической частотой
С. Начальной
фазойD. Фазой
Слайд 27 10. Длину нити математического маятника увеличили в 4
раза, а амплитуду колебаний уменьшили в 2 раза. Как
изменится период колебаний маятника?А. Уменьшится в 4 раза
В. Уменьшится в 2 раза
С. Не изменится
D. Увеличится в 2 раза
Слайд 28 11. Период колебаний пружинного маятника равен Т. Массу
маятника увеличили в 4 раза. Как изменился период колебаний?
А.
Увеличился в 4 разаВ. Уменьшился в 4 раза
С. Не изменился
D. Увеличился в 2 раза
Слайд 29 12. Какое из перечисленных ниже действий позволит уменьшить
частоту колебаний математического маятника?
А. Уменьшение длины подвеса
В. Увеличение амплитуды
колебанийС. Увеличение массы груза
D. Увеличение длины подвеса
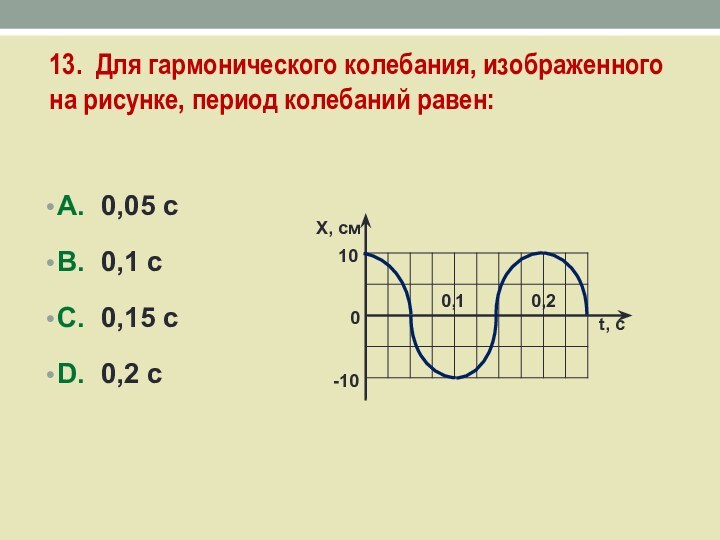
Слайд 30 13. Для гармонического колебания, изображенного на рисунке, период
колебаний равен:
А. 0,05 с
В. 0,1 с
С. 0,15 с
D. 0,2
cХ, см
10
0
-10
t, c
0,1
0,2
Слайд 31 14. Материальная точка совершает колебания по закону: смещение точки
через t = 0,1 с равно…
А. 0 м
В.
0,2 мС. 0,4 м
D. 1 м
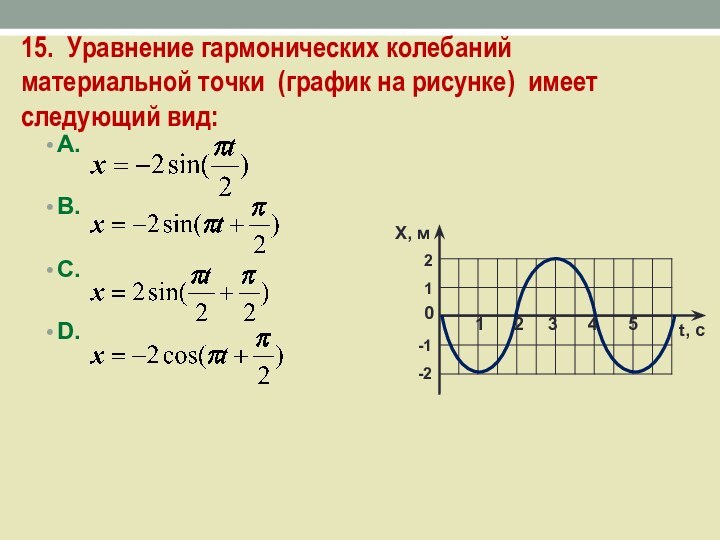
Слайд 32 15. Уравнение гармонических колебаний материальной точки (график на
рисунке) имеет следующий вид:
А.
B.
C.
D.
Х, м
1
2
0
-1
-2
1
2
3
4
5
t, c
Слайд 33 16. Маятниковые часы идут на поверхности Луны в
2,46 раз медленнее, чем на Земле. Ускорение свободного падения
на Луне равно…А. 3,98 м/с²
В. 1,62 м/с²
С. 24,1 м/с²
D. 6,25 м/с²