- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Коллоидно-химические свойства и методы определения дисперсности НДС. Лекция 3
Содержание
- 2. Особенности нефтяных дисперсных систем Большая удельная
- 3. Удельная поверхность НДСS уд. =S /М, м2/кг Для
- 4. Влияние размеров дисперсных частиц на свойства НДС
- 5. Размерные эффектыСхема образования избыточного давления (закон Лапласа)
- 6. Уравнение давления насыщенного пара над плоской P∞
- 7. т.е. растворимость малых частиц выше растворимости крупныхУравнение
- 8. Лиофильные и лиофобные поверхности0< θ90 ºС – лиофобные поверхности (гидрофобные или олеофобные)
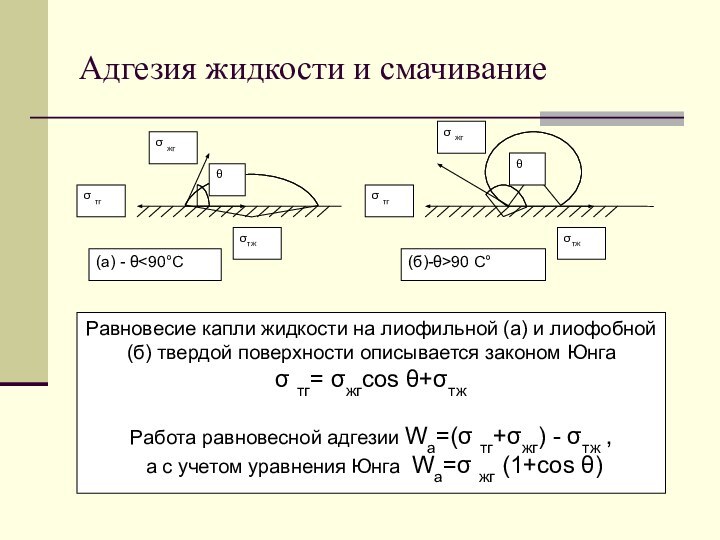
- 9. Адгезия жидкости и смачивание
- 10. Капиллярные явления в пористых телах В капилляре за счет смачивания (угол θ
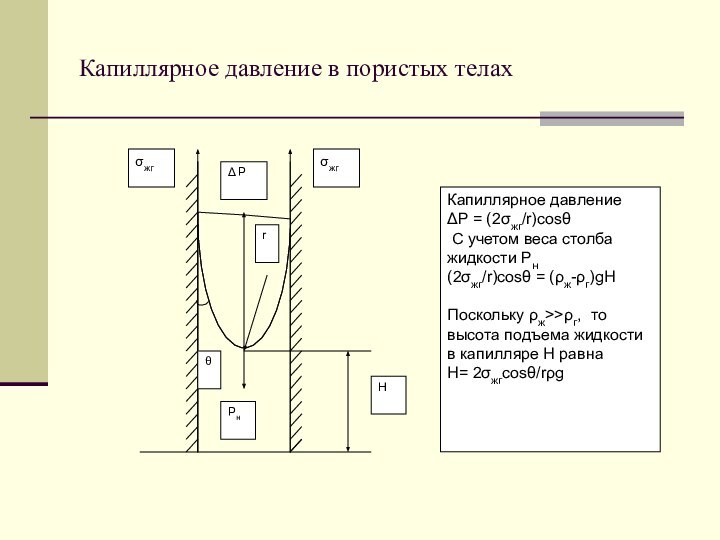
- 11. Капиллярное давление в пористых телах
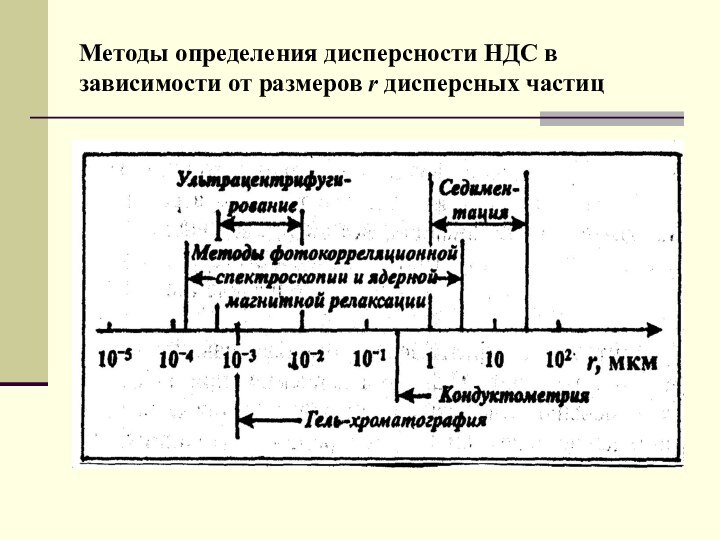
- 13. Методы определения дисперсности НДС в зависимости от размеров r дисперсных частиц
- 14. Интегральные и дифференциальные параметры .Интегральные параметры дают
- 15. Нижний предел измерения размеров частиц различными методами1- глаз человека; 2 -седиментация; 3 -оптический микроскоп; 4 -рассеяние света
- 16. Определение размеров частиц НДС методом турбидиметрии Закон
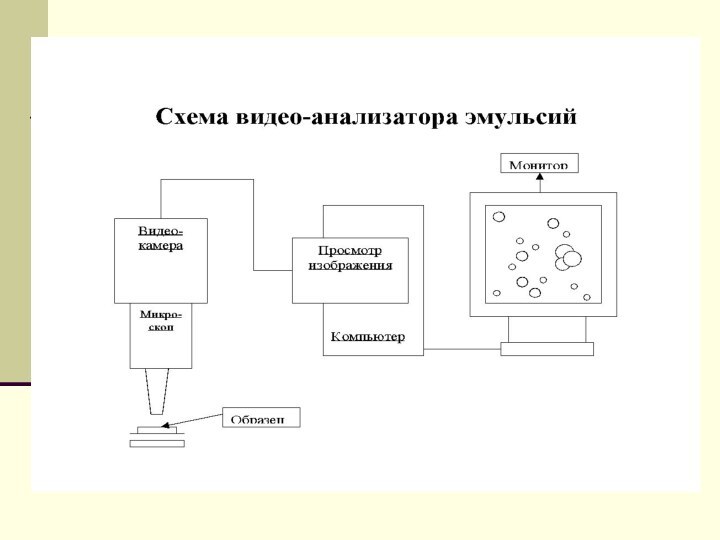
- 17. Устройство кондуктометрического счетчика прибора фирмы "Coulter
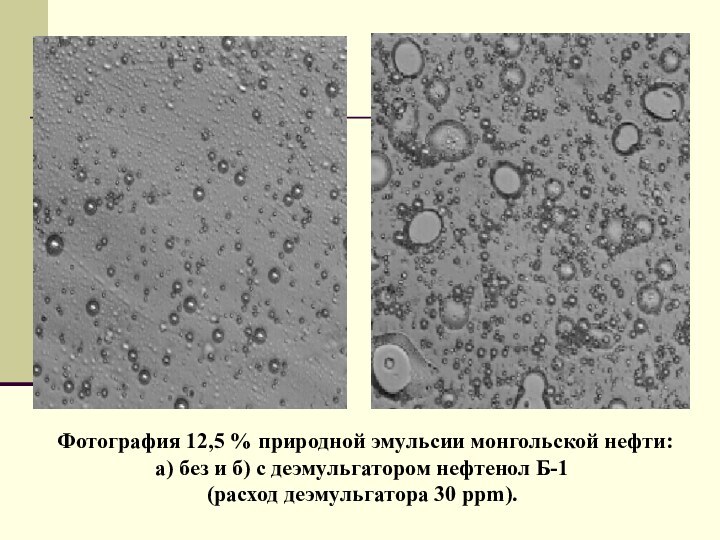
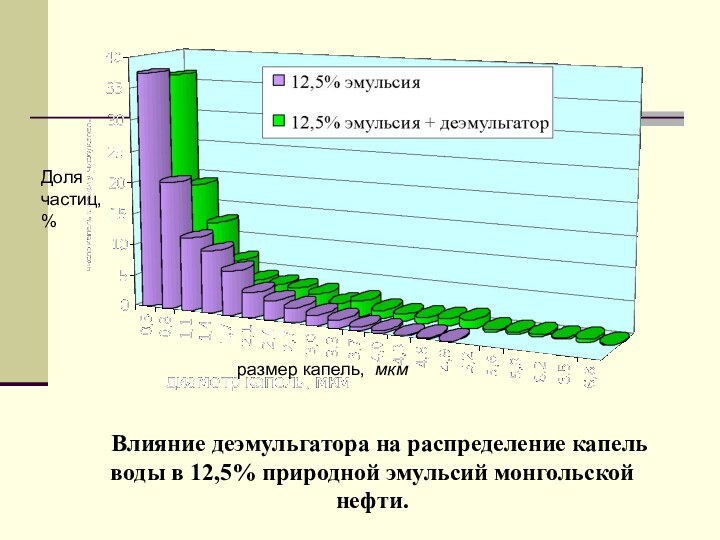
- 19. Фотография 12,5 % природной эмульсии монгольской нефти:а)
- 20. Скачать презентацию
- 21. Похожие презентации
Особенности нефтяных дисперсных систем Большая удельная поверхность (Sуд.)Избыток поверхностной энергии (σ)Дополнительный избыток поверх-ностной энергии на выпуклой поверх-ности раздела фаз ΔР (закон Лапласа)









Слайд 2
Особенности
нефтяных дисперсных систем
Большая удельная поверхность (Sуд.)
Избыток
поверхностной энергии (σ)
раздела фаз ΔР (закон Лапласа)
Слайд 3
Удельная поверхность НДС
S уд. =S /М, м2/кг
Для частиц
одного и того же размера r
S уд. =
S1n,где n - число частиц в 1 кг дисперсной фазы.
Число сферических части в 1 кг дисперсной фазы
n =(4/3 πr3ρ) -1
Учитывая, что поверхность сферических частиц равна 4πr2 , получаем
S уд. =3/ rρ
Слайд 4 Влияние размеров дисперсных частиц на свойства НДС (наноразмерные
эффекты)
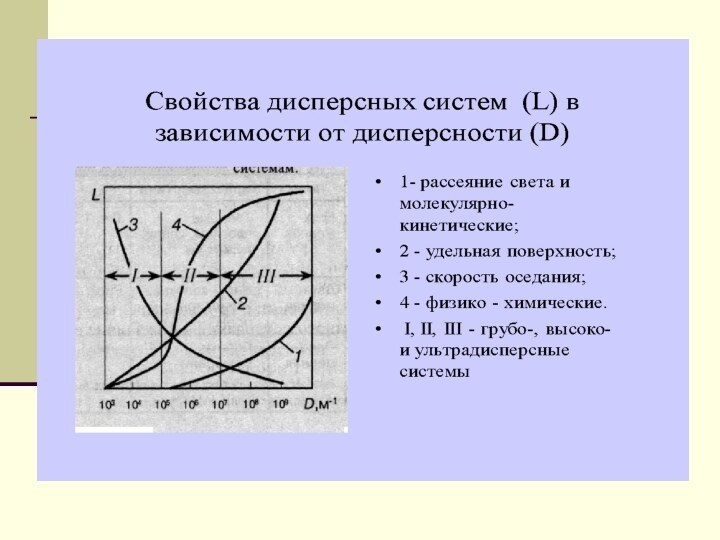
Свойства ультрадисперсных и высокодисперсных НДС зависят не только от
химического состава образующего их вещества, но и от размера частиц. Такую зависимость называют размерным, или масштабным, эффектом.
Различают две группы размерных эффектов:
1. Эффекты, связанные с кривизной поверхности жидкой или газовой дисперсной частицы
2. Изменения физических и химических свойств, обусловленные малыми размерами дисперсных частиц
Слайд 5
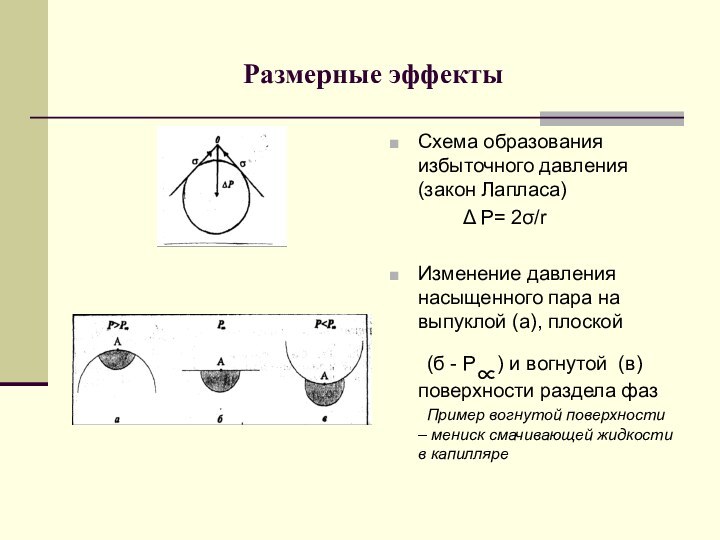
Размерные эффекты
Схема образования избыточного давления (закон Лапласа)
Δ P=
2σ/rИзменение давления насыщенного пара на выпуклой (а), плоской
(б - Р∝) и вогнутой (в) поверхности раздела фаз
Пример вогнутой поверхности – мениск смачивающей жидкости в капилляре
Слайд 6 Уравнение давления насыщенного пара над плоской P∞ и
искривленной Р поверхностями
Уравнение Кельвина
Ln(P/P∞)
= ± 2σжг Vm/(rRT)Прирост давления насыщенного пара тем больше,
чем меньше размер капель:
ΔР,% r
0,1 1 мкм
1 100 нм
10 10 нм
Слайд 7
т.е. растворимость малых частиц выше
растворимости крупных
Уравнение зависимости
растворимости
частиц C(r) от размера r
При разложении в ряд
получаем
Слайд 8
Лиофильные и лиофобные поверхности
0< θ
(гидрофильные или олеофильные)
θ>90 ºС – лиофобные поверхности (гидрофобные
или олеофобные)
Слайд 10
Капиллярные явления в пористых телах
В капилляре за счет
смачивания
(угол θ
σжг на искривленной поверхности с радиусом кривизны r вызывает капиллярное давление ΔP , которое уравновешивается весом столба жидкости Pн
Слайд 14
Интегральные и дифференциальные параметры .
Интегральные параметры дают усредненные
характеристики частиц − радиуса r или диаметра d, удельной
поверхности s, среднего объема сферических частиц V и др.r = Σ fi ri /ni; s= 4πΣfi ri 2/ni ; V=πΣ(fi di 3/6ni) ,
где fi − частота вероятности появления частиц с радиусом ri
в поле зрения;
n, ni − общее число измеряемых частиц или
число частиц в i-ом интервале размеров;
ri - средний размер частиц в i-ом интервале размеров.
В случае полидисперсных частиц наиболее полную и достоверную информацию об ансамбле частиц дают дифференциальные характеристики. Результаты дисперсионного анализа обычно представляют в форме дифференциальных кривых распределения частиц по размерам
Слайд 15
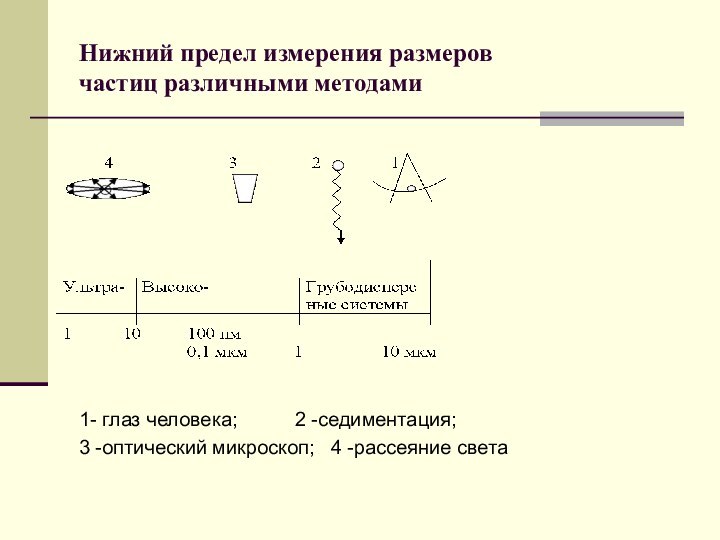
Нижний предел измерения размеров
частиц различными методами
1- глаз
человека; 2 -седиментация;
3 -оптический микроскоп; 4 -рассеяние света
Слайд 16
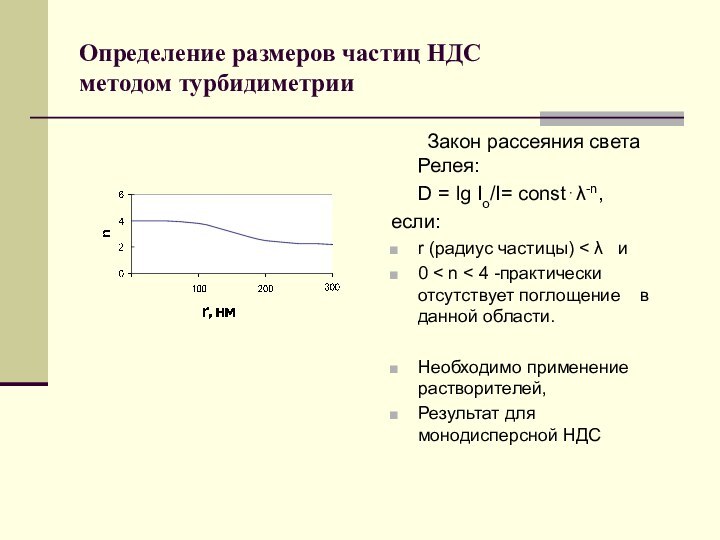
Определение размеров частиц НДС
методом турбидиметрии
Закон рассеяния света
Релея:
D = lg Io/I= const⋅λ-n,
если:
r (радиус частицы) < λ и
0 < n < 4 -практически отсутствует поглощение в данной области.
Необходимо применение растворителей,
Результат для монодисперсной НДС
Слайд 17
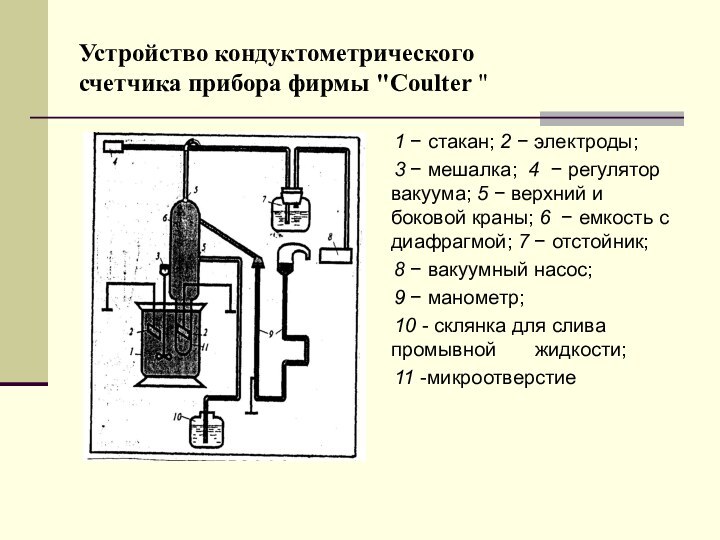
Устройство кондуктометрического
счетчика прибора фирмы "Coulter "
1 −
стакан; 2 − электроды;
3 − мешалка; 4 −
регулятор вакуума; 5 − верхний и боковой краны; 6 − емкость с диафрагмой; 7 − отстойник; 8 − вакуумный насос;
9 − манометр;
10 - склянка для слива промывной жидкости;
11 -микроотверстие





























