Слайд 2
Итак, в неклассической версии ЕНКМ:
учет
стохастических воздействий и вызываемых ими флуктуаций требует использования вероятностного
описания природы.
Это означает отказ от детерминистского взгляда на природу, который несовместим с понятием случайности.
Слайд 3
Квантовые состояния
«холодное окружение»
Т=0
В этих условиях объект
называется квантоном
Слайд 4
П.А.-М. Дирак (1902-1984) -основатель современных квантовых идей
Нобелевская премия
1934 г.
Слайд 5
В неклассической ЕНКМ исходят из того, сто под
влиянием стохастического воздействия все характеристики объекта являются случайными.
При
описании квантовых явлений нельзя использовать модель изолированного объекта, как это делается в классике. Термин «свободный объект" следует понимать только как отсутствие регулярного воздействия сил и полей.
Так чем же обусловлено квантовое воздействие, если при Т=0 тепловое движение в окружении объекта полностью заморожено, нет столкновений с молекулами окружения и никаких внешних сил?
Слайд 6
Но отсутствие молекул вещества еще не означает
полную пустоту. В этом случае объект окружён физическим вакуумом.
Это огромный резервуар, заполненный океаном виртуальных частиц, обладающих энергией и импульсом.
При Т=0 вакуум беспорядочно воздействует на объект, вызывая при этом флуктуации его характеристик и особенности поведения. Если не учитывать стохастическое воздействие вакуума, то невозможно объяснить, откуда же тогда берутся все те «чудесные» свойства, которые "вдруг" проявляет объект, ни с чем не взаимодействующий в привычном классическом смысле.
Слайд 7
Определяющая роль стохастического воздействия в поведении квантона, или
о странностях квантона по сравнению с классическими частицами
Слайд 8
Они обнаруживают очень «необычное» поведение
Быть может, эти электроны
–
Миры, где пять материков,
Искусства, знанья, войны, троны
И память
сорока веков.
Еще, быть может, каждый атом –
Вселенная, где сто планет;
Там все, что здесь, в объеме сжатом,
Но также то, чего здесь нет….
В. Брюсов. Мир ЭЛЕКТРОНА.
Собр.соч. в 7-и тт. Т. 3. С. 172.
М.: Худ. лит., 1974.
Слайд 9
Пример необычного поведения свободного электрона, описываемого моделью
квантона
Свободная электрон в классическом подходе должен двигаться равномерно и
прямолинейно, т.е. с постоянной скоростью V=const, что соответствует линейной зависимости координаты от времени x=Vt. График этой зависимости – прямая линия.
Однако при скоростях, сравнимых со скоростью света, его скорость перестает быть константой. Она начинает быстро флуктуировать вокруг среднего значения с частотой приблизительно 1,6·1021 Гц.
Слайд 10
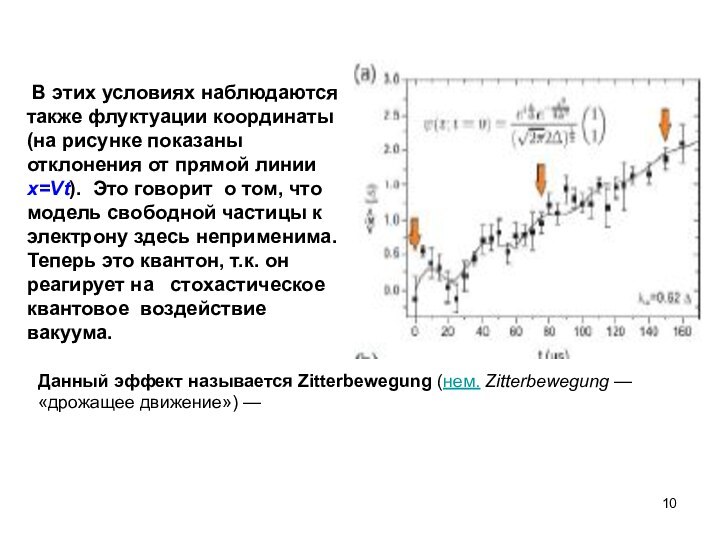
В этих условиях наблюдаются также флуктуации координаты
(на рисунке показаны отклонения от прямой линии x=Vt). Это
говорит о том, что модель свободной частицы к электрону здесь неприменима. Теперь это квантон, т.к. он реагирует на стохастическое квантовое воздействие вакуума.
Данный эффект называется Zitterbewegung (нем. Zitterbewegung — «дрожащее движение») —
Слайд 11
ПОВЕДЕНИЕ КЛАССИЧЕСКОГО ОБЪЕКТА
(не испытывает
стохастического воздействия)
КУДА ПОЛЕТИТ МЯЧ?
ОН ЛИБО ПРОЛЕТИТ НАД ВОРОТАМИ, ЛИБО БУДЕТ ЗАБИТ ГОЛ
ПРОЛЕТАЯ ВЫШЕ ВОРОТ, МЯЧ НЕ «ОЩУЩАЕТ» ИХ.
ПОПАДАЯ В ВОРОТА, МЯЧ МОЖЕТ ОТРАЗИТЬСЯ ОТ СЕТКИ, НО НЕ МОЖЕТ ОКАЗАТЬСЯ ЗА ПРЕДЕЛАМИ ПОЛЯ
Слайд 12
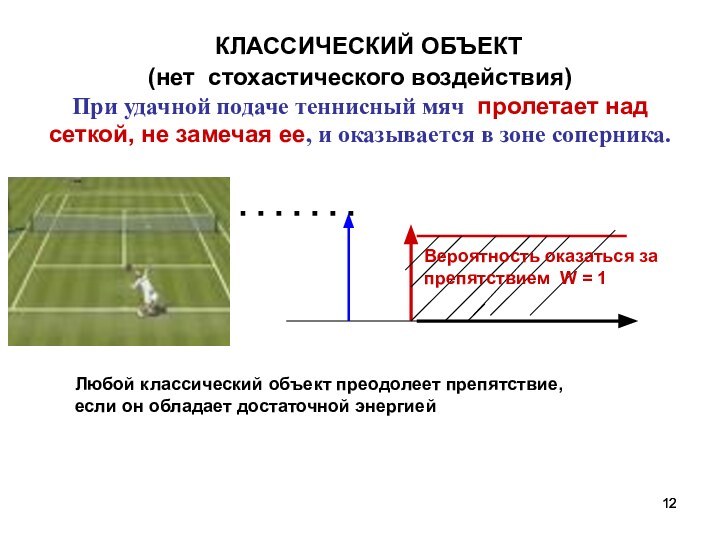
КЛАССИЧЕСКИЙ ОБЪЕКТ
(нет стохастического воздействия)
При удачной подаче теннисный мяч пролетает над сеткой, не замечая ее, и оказывается в зоне соперника.
Вероятность оказаться за препятствием W = 1
Любой классический объект преодолеет препятствие, если он обладает достаточной энергией
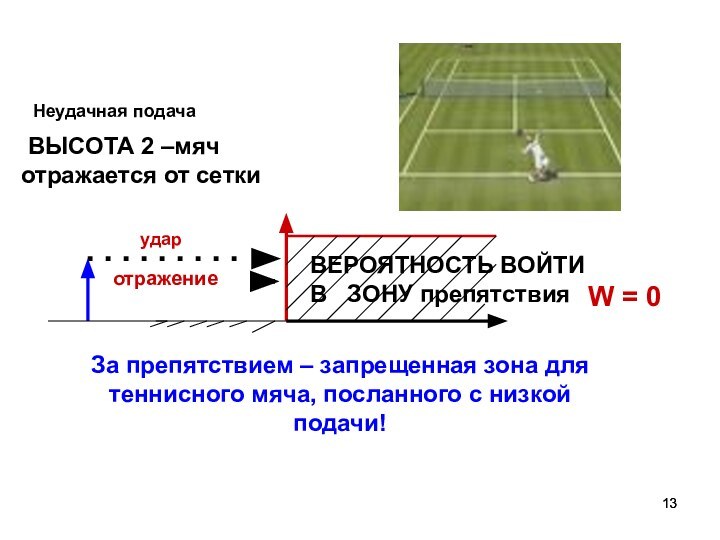
W = 0
ВЕРОЯТНОСТЬ ВОЙТИ
В ЗОНУ препятствия
ВЫСОТА 2 –мяч отражается от сетки
За препятствием – запрещенная зона для теннисного мяча, посланного с низкой подачи!
отражение
удар
Неудачная подача
Слайд 14
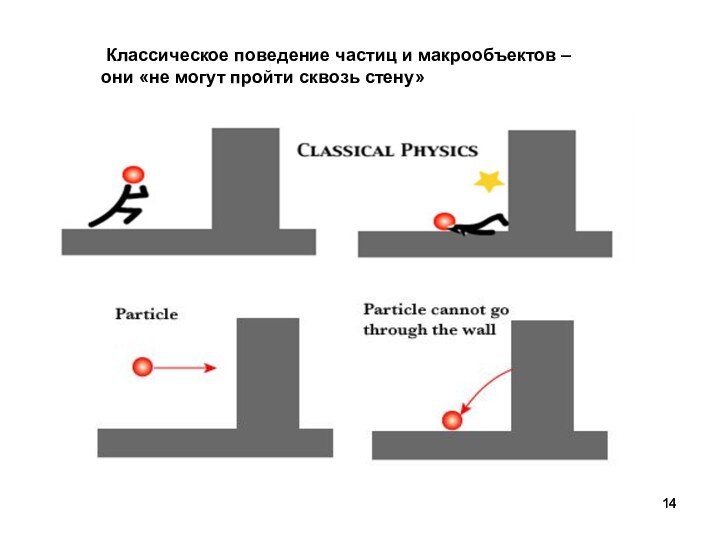
Классическое поведение частиц и макрообъектов –
они «не могут
пройти сквозь стену»
Слайд 15
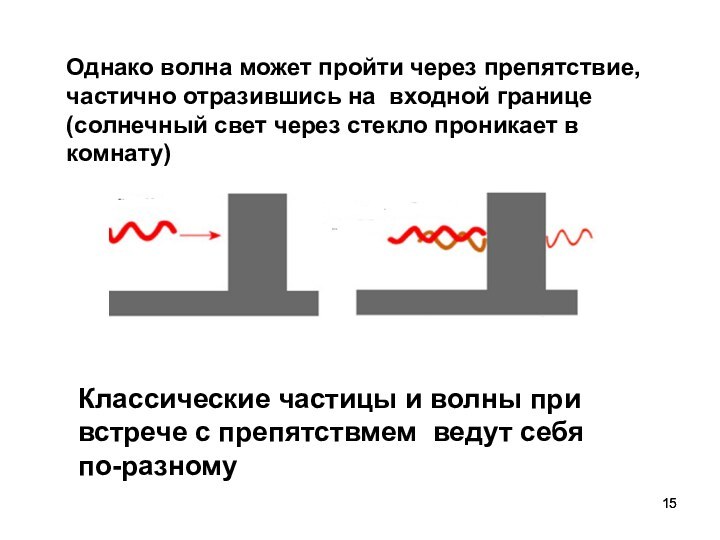
Однако волна может пройти через препятствие, частично отразившись
на входной границе (солнечный свет через стекло проникает в
комнату)
Классические частицы и волны при встрече с препятствмем ведут себя по-разному
Слайд 16
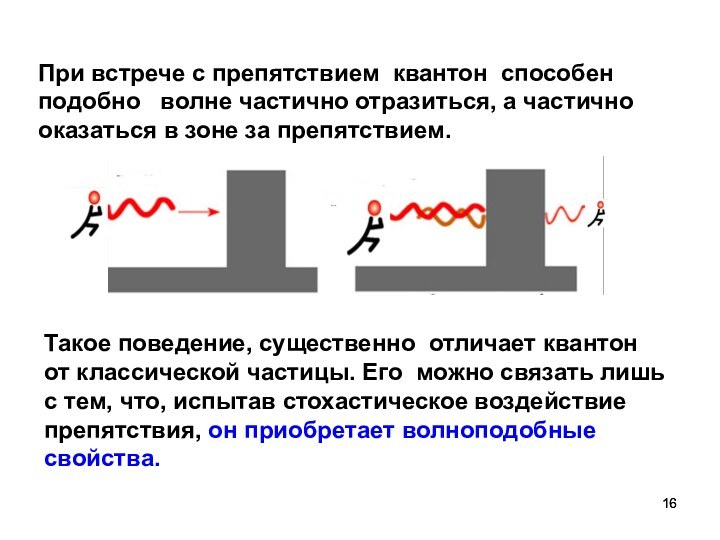
При встрече с препятствием квантон способен подобно
волне частично отразиться, а частично оказаться в зоне за
препятствием.
Такое поведение, существенно отличает квантон от классической частицы. Его можно связать лишь с тем, что, испытав стохастическое воздействие препятствия, он приобретает волноподобные свойства.
Слайд 17
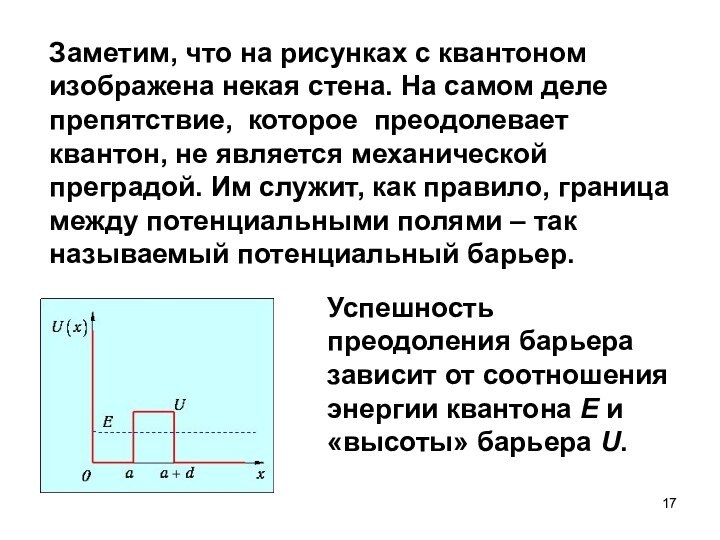
Заметим, что на рисунках с квантоном изображена некая
стена. На самом деле препятствие, которое преодолевает квантон, не
является механической преградой. Им служит, как правило, граница между потенциальными полями – так называемый потенциальный барьер.
Успешность преодоления барьера зависит от соотношения энергии квантона E и «высоты» барьера U.
Слайд 18
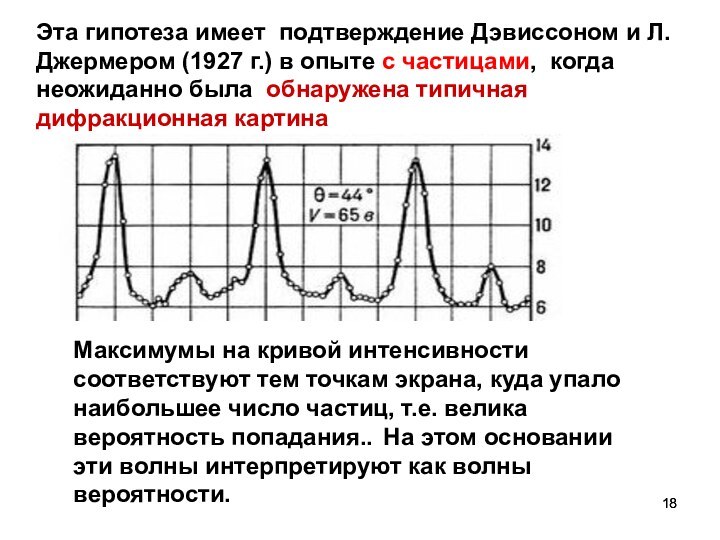
Эта гипотеза имеет подтверждение Дэвиссоном и Л. Джермером
(1927 г.) в опыте с частицами, когда неожиданно была
обнаружена типичная дифракционная картина
Максимумы на кривой интенсивности соответствуют тем точкам экрана, куда упало наибольшее число частиц, т.е. велика вероятность попадания.. На этом основании эти волны интерпретируют как волны вероятности.
Слайд 19
Дифракция - свидетельство особого волнового процесса, который
в данном случае порождается движущимися частицами (напр., электронами)
Природа
этого процесса необычна (противоречивое сочетание волны и частицы, что невозможно в классике).
Для интерпретации природы этих волн необходимо обсудить их особенности
Слайд 20
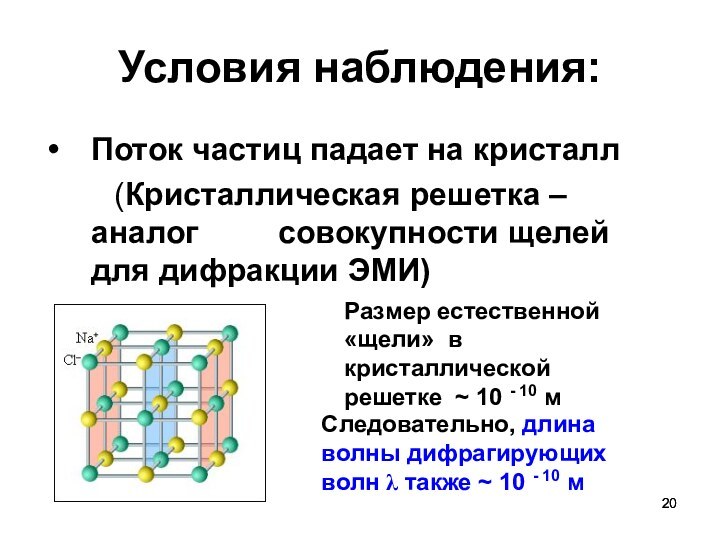
Условия наблюдения:
Поток частиц падает на кристалл
(Кристаллическая решетка – аналог
совокупности щелей для дифракции ЭМИ)
Размер естественной «щели» в кристаллической решетке ~ 10 - 10 м
Следовательно, длина волны дифрагирующих волн λ также ~ 10 - 10 м
Слайд 21
Волна, которая связана с микрочастицей, называется
волной де Бройля
Луи де Бройль
(1892-1987), Нобелевский лауреат 1929г.
Франция
Эксперимент подтверждает .ю что длина волны де-Бройля
Здесь ħ- постоянная Планка, а величина λ ~ равна периоду кристаллической решётки, на которой наблюдается дифракция, p- импульс частицы.
характеристикой микрочастицы) и λ (характеристикой состояния микрочастицы, формируемого окружением).
Это соотношение указывает на связь между р (корпускулярной
Слайд 22
Особенности дифракции частиц
Эффект наблюдается для любых
микрочастиц (с зарядом и нейтральных)
След., природа этого процесса не
связана с электромагнитными волнами.
Волновые свойства проявляются и у свободных (в классическом смысле) микрочастиц.
След., природа этого процесса не связана с механическими волнами, т.е. с процессами, вызванными механическими возмущениями.
Итак, экспериментально доказано, что при движении любых микрочастиц проявляются волновые свойства.
Слайд 23
Дифракция микрочастиц происходит, если
1. Через «щель»
одновременно проходит «поток» микрочастиц
2. Одну и ту же
частицу поочередно возвращать в исходное положение перед щелью
Одна микрочастица в одиночном опыте со щелью не создает дифракционной картины.
Слайд 24
NВ
Волновые свойства возникают только в коллективе N
одинаковых событий, происходящих в одних и тех же условиях
Этот
коллектив называется неклассическим статистическим ансамблем
Корректно использовать теорию вероятностей можно только в случае, когда N∞.
Слайд 25
Классические представления не работают. Необходимо обращение к
неклассическим
идеям о стохастическом воздействии
В момент прохождения условной
«щели» частицы испытывают стохастическое квантовое воздействие
Возникает ансамбль квантонов и образуется дифракционная картина.
Направление импульса (и скорости) квантона становится случайным.
В случае ансамбля квантонов возникает устойчивая дифракционная картина
Слайд 26
В опыте по дифракции одиночной микрочастицы на щели
нельзя однозначно предсказать координату квантона х после прохождения щели.
Это случайная характеристика.
Координату квантона x после щели можно предсказать только через указание вероятности W(x) ее попадания в определенную точку экрана x ,
С помощью теории вероятностей для случайных величин находят средние значения характеристик и отклонения от них.
Импульс и скорость способны испытывать флуктуации, характеризуемые дисперсией
Слайд 27
Ансамбль квантонов описывается вероятностным образом через величину Ψ(x),
называемую амплитудой вероятности, или волновой функцией. Она может быть
комплекской функцией.
Вероятность события W(х) , при котором одиночный квантон попадет в точку экрана с координатой х связана с амплитудой вероятности Ψ(x)| следующим соотношением: W(х) = |Ψ(x)|2 .
Так как вероятность – действительная и сугубо положительная величина, в этой формуле амплитуда вероятности берётся по модулю: |Ψ(x)|2 = Ψ*(x) Ψ(x), где символ * означает комплексное сопряжение
Слайд 28
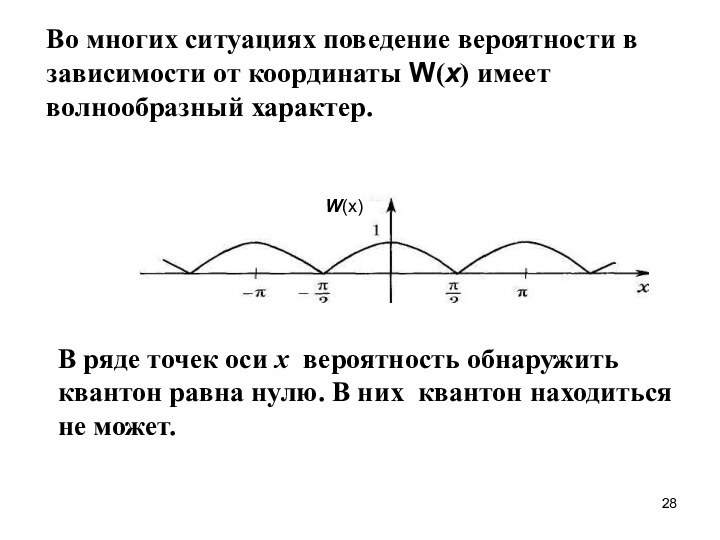
Во многих ситуациях поведение вероятности в зависимости от
координаты W(х) имеет волнообразный характер.
В ряде точек оси x
вероятность обнаружить квантон равна нулю. В них квантон находиться не может.
Слайд 29
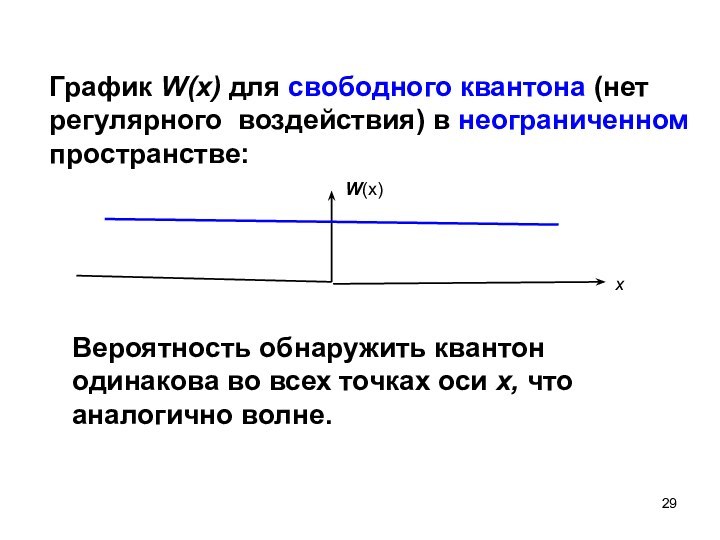
График W(x) для свободного квантона (нет регулярного
воздействия) в неограниченном пространстве:
W(x)
x
Вероятность обнаружить квантон одинакова во всех
точках оси x, что аналогично волне.
Слайд 30
Как узнать вероятность W(x)?
1. Определить из опыта;
2. Вычислить
теоретически, решая знаменитое уравнение, предложенное Э.Шредингером.
Э. Шрёдингер 1887-1961
(Нобелевская премия
1933 г.)
Слайд 31
Уравнение Шредингера
позволяет непосредственно найти волновую функцию Ψ(x)
квантона, а через нее и вероятность W(x) для целого
ряда конкретных ситуаций
Для квантовых состояний уравнение Шредингера играет роль, аналогичную роли уравнения второго закона Ньютона в классической физике.
Слайд 32
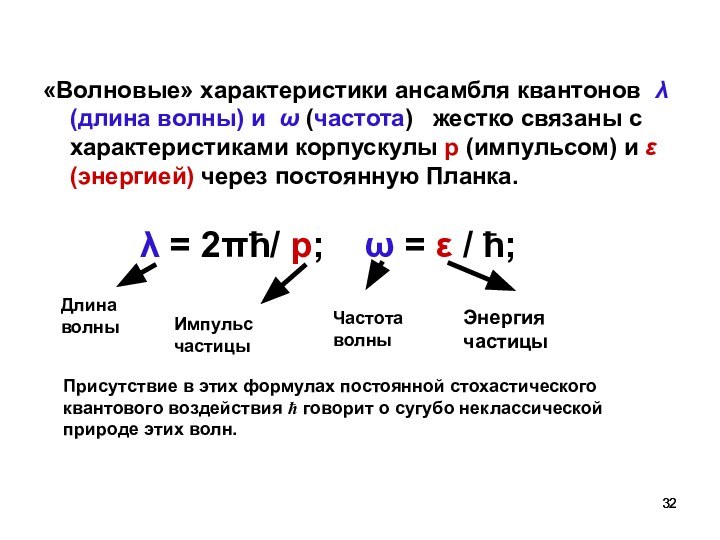
«Волновые» характеристики ансамбля квантонов λ (длина волны) и
ω (частота) жестко связаны с характеристиками корпускулы р
(импульсом) и ε (энергией) через постоянную Планка.
λ = 2πћ/ р; ω = ε / ћ;
Длина волны
Импульс частицы
Частота волны
Энергия частицы
Присутствие в этих формулах постоянной стохастического квантового воздействия ħ говорит о сугубо неклассической природе этих волн.
Слайд 33
Постоянная Планка –фундаментальная константа квантового стохастического воздействия
= 1,06 ·10-34 Дж · сек
Она характеризует
минимальное значение квантового стохастического воздействия окружения на объект
Слайд 34
в собранном «загоне» видны стоячие волны электронной плотности
захваченного ловушкой электрона
«Наблюдение» волн вероятности
«квантовый
загон» для электрона из атомов железа на поверхности кремния
Волны де Бройля могут быть стоячими (в ограниченной области) и бегущими (в свободном пространстве)
Слайд 35
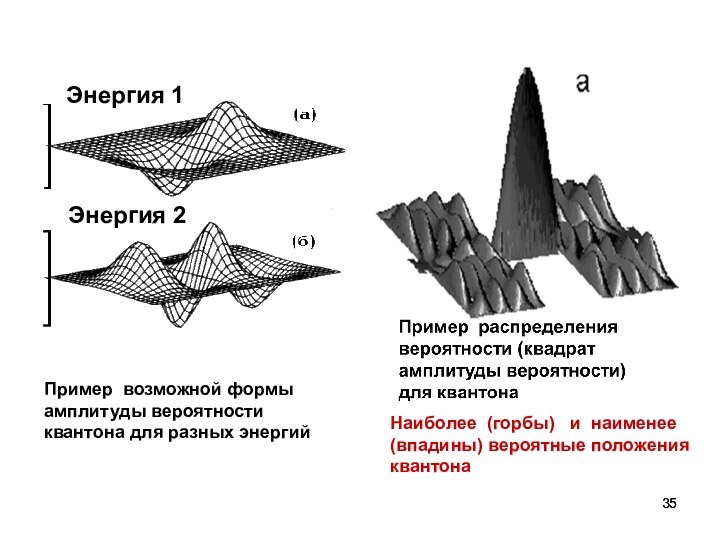
Энергия 1
Энергия 2
Пример возможной формы амплитуды вероятности
квантона для разных энергий
Наиболее (горбы) и наименее (впадины)
вероятные положения квантона
Слайд 36
Особенность квантовых состояний:
Квантон может одновременно
находиться в нескольких квантовых состояниях:
и в состоянии |1› и в состоянии |2›: состояние |3› = C1 |1› + C2 |2›;
возникает «смесь» (суперпозиция) состояний, осуществляемых с разными вероятностями: W1 =|C1|2 ; W2 =|C2|2
Однако в эксперименте обнаруживается только одно из двух возможных состояний. Как правило, это будет состояние, вероятность которого больше.
Слайд 37
Природа диктует нам НЕКЛАССИЧЕСКУЮ ЛОГИКУ
квантон может одновременно
находиться в разных точках пространства : и здесь, и
там, и сям.
Одновременное сочетание нескольких альтернативных возможностей – признак неклассической логики
Логика «и-и»
(идея дополнительности!)
Слайд 38
В классической логике это невозможно–
Всегда есть альтернатива:
или здесь, или там
Классическая логика
основана на выборе одной из альтернативных возможностей.
Это логика или-или
Слайд 39
Парадокс кота Шрёдингера
Пока атом не распался, с котом
всё в порядке,
В закрытом ящике находится кот.
В том же ящике : - атом радиоактивного изотопа, - счётчик продуктов распада, - молоток, разбивающий ампулу с ядом при срабатывании счетчика
Слайд 40
Далее вступает в силу вероятностный характер квантового состояния.
Неизвестно,
когда атом распадётся. В каждый данный момент имеется лишь
определённая вероятность его распада.
В каждый данный момент атом находится в суперпозиции двух квантовых состояний: состояния, когда он ещё не распался, и состояния, когда он уже распался.
Слайд 41
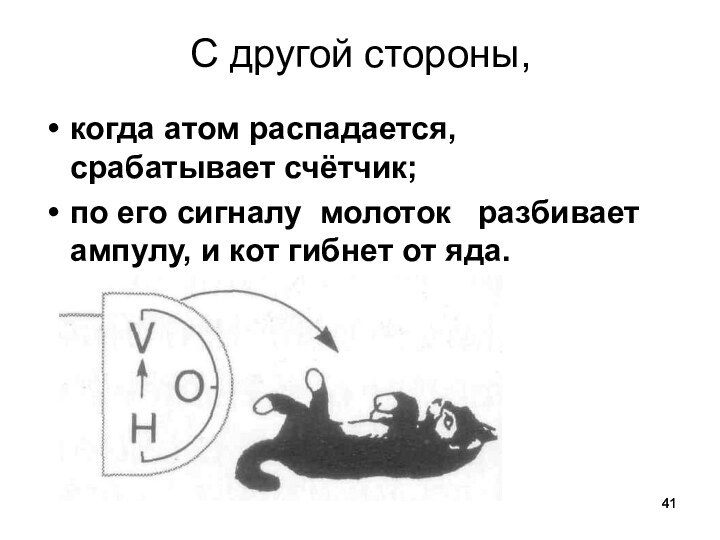
С другой стороны,
когда атом распадается, срабатывает
счётчик;
по его сигналу молоток разбивает ампулу, и
кот гибнет от яда.
Слайд 42
подходя к закрытому ящику, мы должны считать, что
система (атом- кот) находится в суперпозиции двух состояний:
Возникающий nonsense
является парадоксом лишь для макроскопического тела, каким является кот
нераспавшийся атом и живой кот
распавшийся атом и мёртвый кот.
+
В микромире – это обыденное явление
Слайд 43
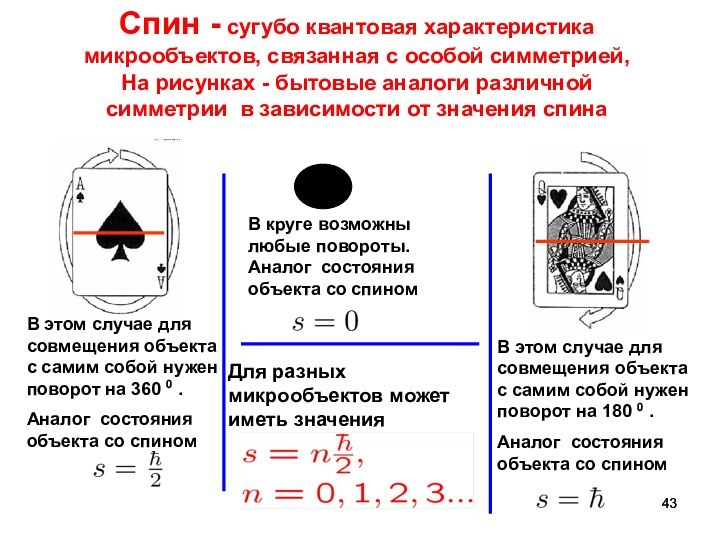
Спин - сугубо квантовая характеристика микрообъектов, связанная с
особой симметрией,
На рисунках - бытовые аналоги различной симметрии в зависимости от значения спина
В этом случае для совмещения объекта с самим собой нужен поворот на 360 0 .
Аналог состояния объекта со спином
В этом случае для совмещения объекта с самим собой нужен поворот на 180 0 .
Аналог состояния объекта со спином
В круге возможны любые повороты. Аналог состояния объекта со спином
Для разных микрообъектов может иметь значения
Слайд 44
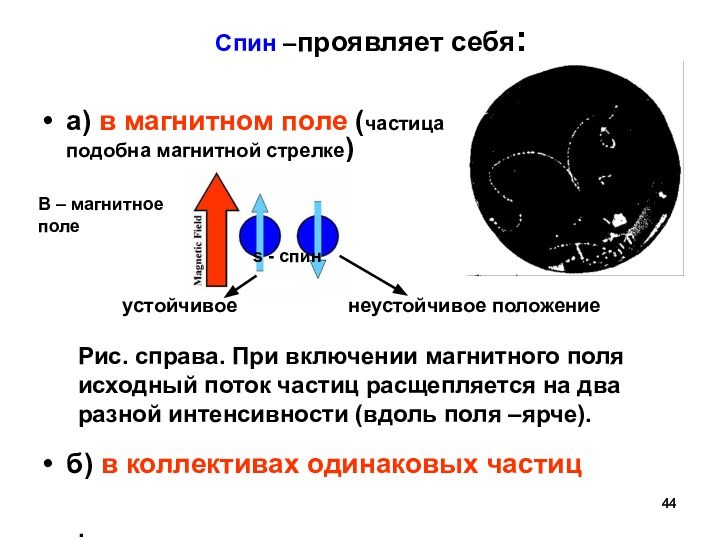
Спин –проявляет себя:
а) в магнитном поле
(частица
подобна магнитной стрелке)
устойчивое неустойчивое положение
б) в коллективах одинаковых частиц
В – магнитное поле
s - спин
Рис. справа. При включении магнитного поля исходный поток частиц расщепляется на два разной интенсивности (вдоль поля –ярче).
.
Слайд 45
В зависимости от величины спина микрообъекты делятся на
бозоны
(фотоны и другие переносчики фунламентальных взаимодействий с нулевой массой):
s = 0, 1ħ, 2ħ, любое чётное число ħ/2 .
фермионы (электроны, протоны, нейтроны и другие частицы с ненулевой массой):
s = ½ ħ, 3/2 ħ, 5/2 ħ, …. (любое нечётное число ħ/2)
- Различие между фермионами и бозонами проявляется в коллективном поведении тождественных квантонов.
Слайд 46
Особенность поведения бозонов
Бозоны с полностью идентичными характеристиками
могут пребывать в одном и том же квантовом состоянии
без ограничения их количества. образовывать конденсат.
В этом отношении они ведут себя подобно ансамблю музыкантов, играющих в унисон
Благодаря способности идентичных фотонов (бозонов) скапливаться в одном состоянии, мы наблюдаем мощное когерентное излучение лазеров
Этим свойством объясняется сверхтекучесть и сверхпроводимость жидкого гелия, в котором фермионы-электроны образуют пары и возникает бозонный конденсат. Недавно открыто большое количество новых бозонных конденсатов в различных средах.
Слайд 47
Особенность поведения фермионов
Два и
более фермиона с полностью идентичными характеристиками не могут одновременно
находиться в одном квантовом состоянии! – принцип запрета Паули
В этом отношении фермионы подобны исполнителю-солисту
Между фермионами с рядом одинаковых характеристик должно быть различие хотя бы в ориентации их спинов.
Этому требованию подчиняются электронные состояния в атомах.
Австрийская почтовая марка с портретом Вольфганга Паули
(1900-1958)
Слайд 48
Эвристичность принципа Паули
(Архимед воскликнул «эврика!» (нашёл!). Эвристический
– стиль продуктивного мышления при решении нестандартных задач.
Если всё-таки
все известные характеристики фермионов в одном состоянии совпадают, необходимо вводить новую характеристику, по которой между фермионами будет отличие!
Пример 1. Для различения в нуклоне практически идентичных состояний трех кварков (фермионов) вводится новая трёхзначная характеристика – «цвет» (красный, синий, зелёный) (см. модель нуклона)
Пример 2. Для различения в ядре дейтрона идентичных состояний протона и нейтрона (двух фермионов) вводится новая двузначная характеристика изоспин (±).
Это позволяет глубже проникнуть в свойства микромира
Слайд 49
тепловые
свойства
нанообъектов
10 - 9 м
атомы
молекулы
свойства
ЭМИ
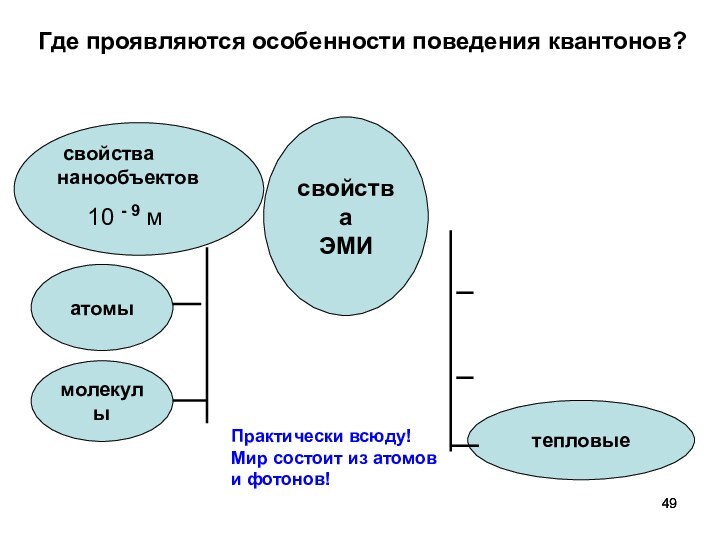
Где
проявляются особенности поведения квантонов?
Практически всюду! Мир состоит из атомов и фотонов!
Слайд 50
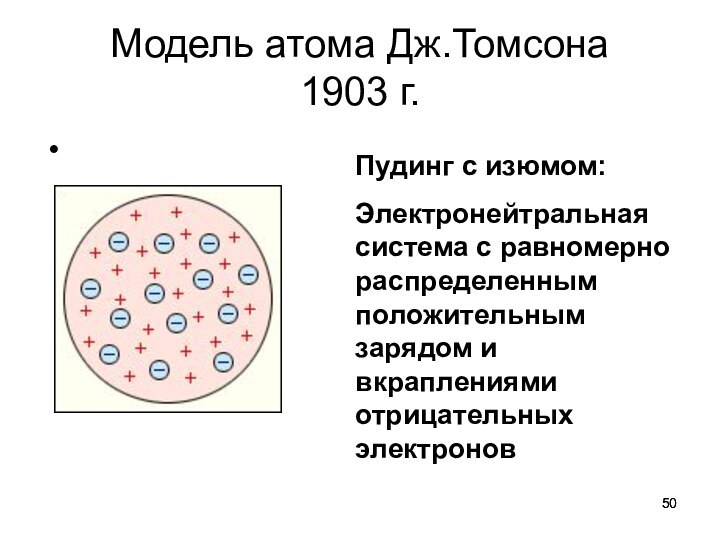
Модель атома Дж.Томсона
1903 г.
Пудинг с изюмом:
Электронейтральная система с равномерно распределенным положительным зарядом и вкраплениями отрицательных электронов
Слайд 51
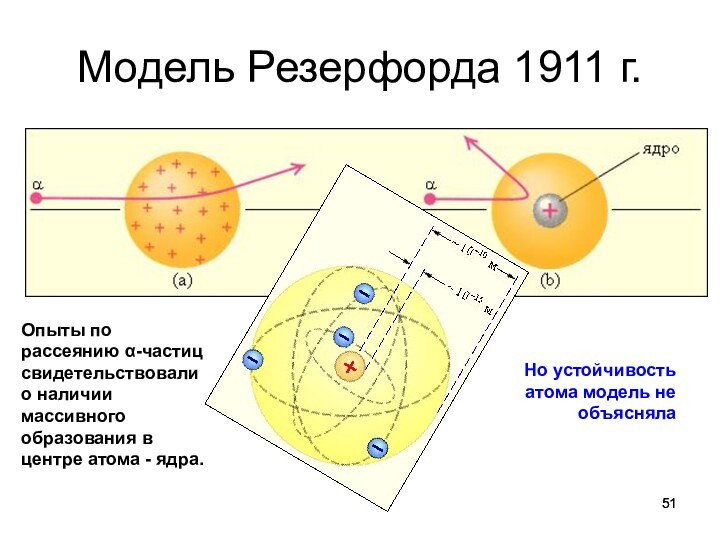
Модель Резерфорда 1911 г.
Опыты по рассеянию α-частиц свидетельствовали
о наличии массивного образования в центре атома - ядра.
Но
устойчивость атома модель не объясняла
Слайд 52
Нильс Бор (1885 - 1962 )
датский ученый,
один из создателей современной физики. Автор основополагающих трудов по
квантовой механике, теории атома, атомного ядра, ядерным реакциям.
Слайд 53
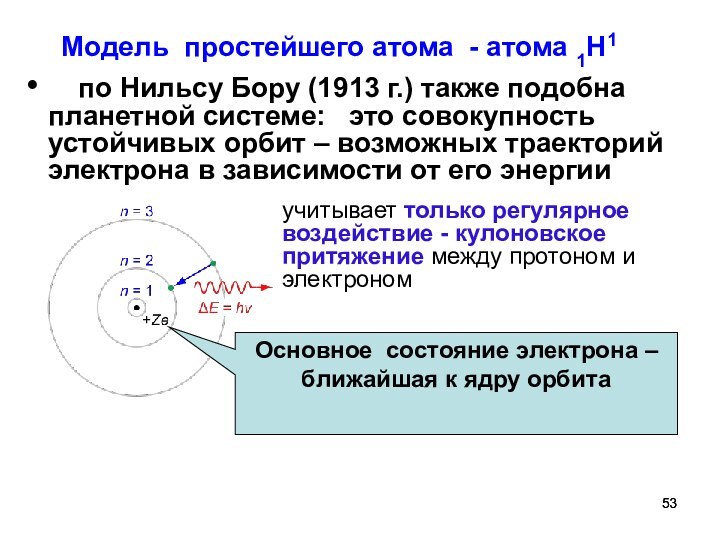
Основное состояние электрона –ближайшая к ядру орбита
Модель простейшего
атома - атома 1Н1
по Нильсу Бору (1913
г.) также подобна планетной системе: это совокупность устойчивых орбит – возможных траекторий электрона в зависимости от его энергии
учитывает только регулярное воздействие - кулоновское притяжение между протоном и электроном
Слайд 54
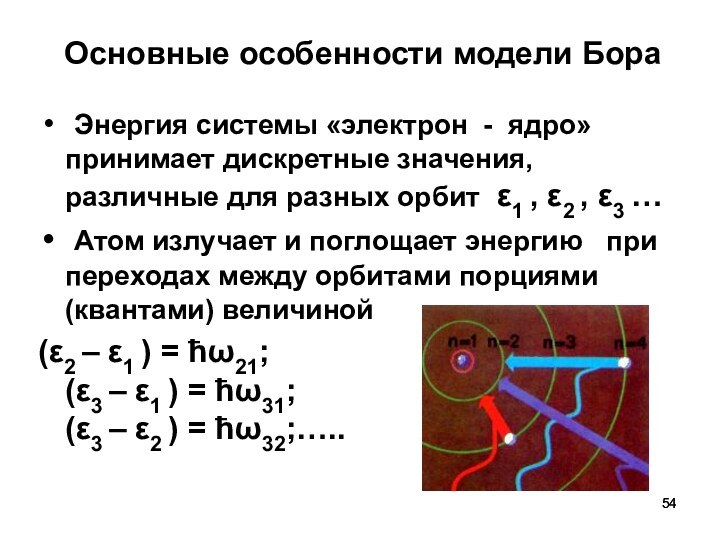
Основные особенности модели Бора
Энергия системы «электрон -
ядро» принимает дискретные значения, различные для разных орбит ε1
, ε2 , ε3 …
Атом излучает и поглощает энергию при переходах между орбитами порциями (квантами) величиной
(ε2 – ε1 ) = ћω21; (ε3 – ε1 ) = ћω31; (ε3 – ε2 ) = ћω32;…..
Слайд 55
Модель Бора - противоречива
– использует понятие электронной орбиты
(определенной траектории) с постоянной энергией.
но движение по ней
должно сопровождаться потерей энергии на излучение, однако модель этого не учитывает - модель непоследовательна
Волновые свойства электрона учитывает только косвенно - на орбите укладывается целое число стоячих волн де Бройля, однако рассматривается только дискретная совокупность разрешенных орбит
Слайд 56
Модель Бора сочетает классические и неклассические положения
- учитывает
только регулярное воздействие - кулоновское притяжение между протоном и
электроном (классический подход),
приписывает электрону дискретные значения энергии (противоречит классике!)
не объясняет многие свойства атомов, наблюдаемые на опыте (в том числе – разнообразие геометрии и наличие объема).
Слайд 57
Современная модель атома водорода как решение уравнения Шрёдингера
ОСОБЕННОСТИ:
Учитывает стохастическое воздействие на электрон со стороны ядра
Электрон - квантон даже в основном состоянии, он адекватно описывается волновой функцией
Электрон может быть обнаружен практически на любом расстоянии от ядра, но с разной вероятностью
Слайд 58
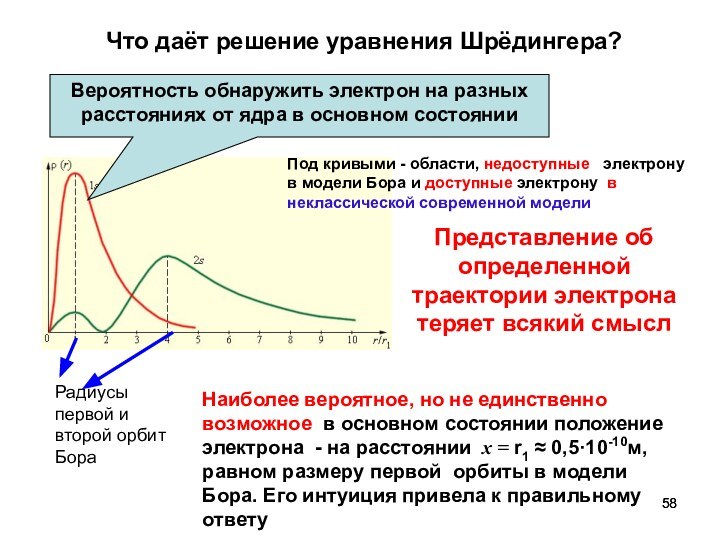
Вероятность обнаружить электрон на разных расстояниях от ядра
в основном состоянии
Под кривыми - области, недоступные электрону
в модели Бора и доступные электрону в неклассической современной модели
Радиусы первой и второй орбит Бора
Наиболее вероятное, но не единственно возможное в основном состоянии положение электрона - на расстоянии x = r1 ≈ 0,5·10-10м, равном размеру первой орбиты в модели Бора. Его интуиция привела к правильному ответу
Представление об определенной траектории электрона теряет всякий смысл
Что даёт решение уравнения Шрёдингера?
Слайд 59
ядро
электронные состояния в атоме
Нечеткость контуров электронных состояний –
свидетельство различной вероятности пребывания электронов в данной области
Слайд 60
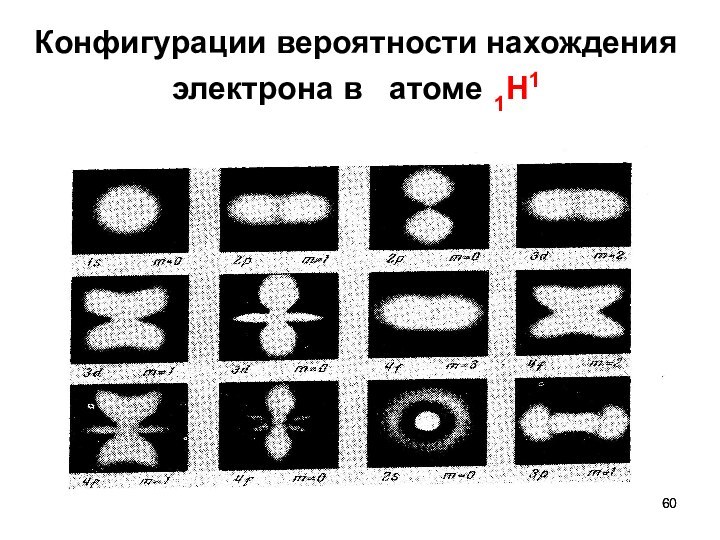
Конфигурации вероятности нахождения электрона в атоме 1Н1
Слайд 61
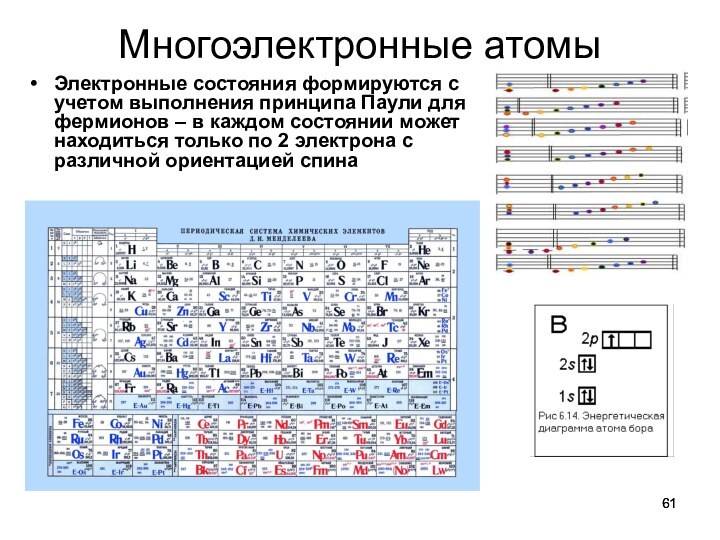
Многоэлектронные атомы
Электронные состояния формируются с учетом выполнения принципа
Паули для фермионов – в каждом состоянии может находиться
только по 2 электрона с различной ориентацией спина
Слайд 62
Современное представление системы Менделеева
Слайд 63
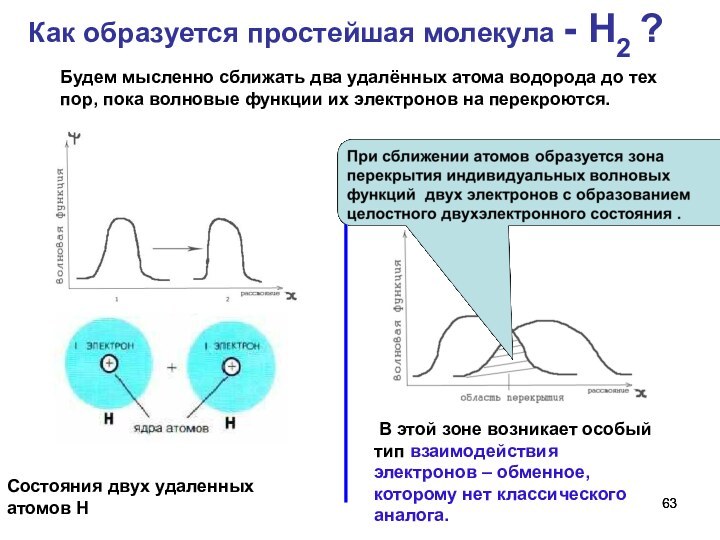
Как образуется простейшая молекула - Н2 ?
Состояния двух удаленных атомов Н
В этой зоне возникает особый тип взаимодействия электронов – обменное, которому нет классического аналога.
Будем мысленно сближать два удалённых атома водорода до тех пор, пока волновые функции их электронов на перекроются.
Слайд 64
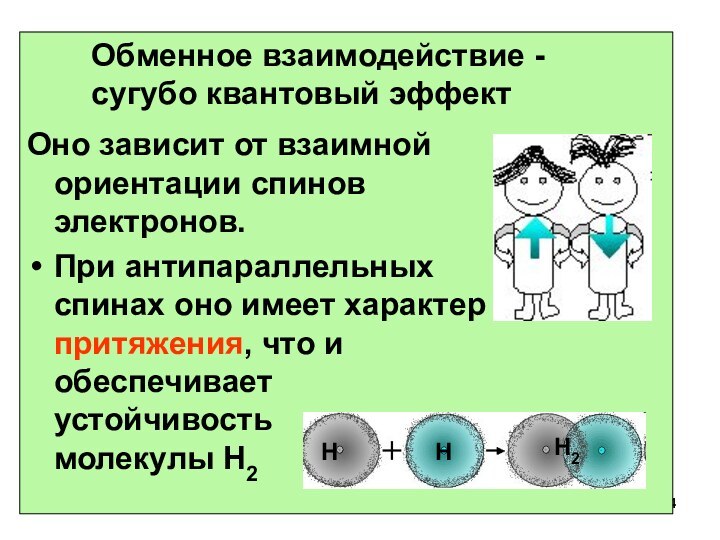
Оно зависит от взаимной
ориентации спинов электронов.
При антипараллельных спинах оно имеет характер притяжения, что и обеспечивает устойчивость молекулы Н2
Н
Н
Н2
Обменное взаимодействие - сугубо квантовый эффект
Слайд 65
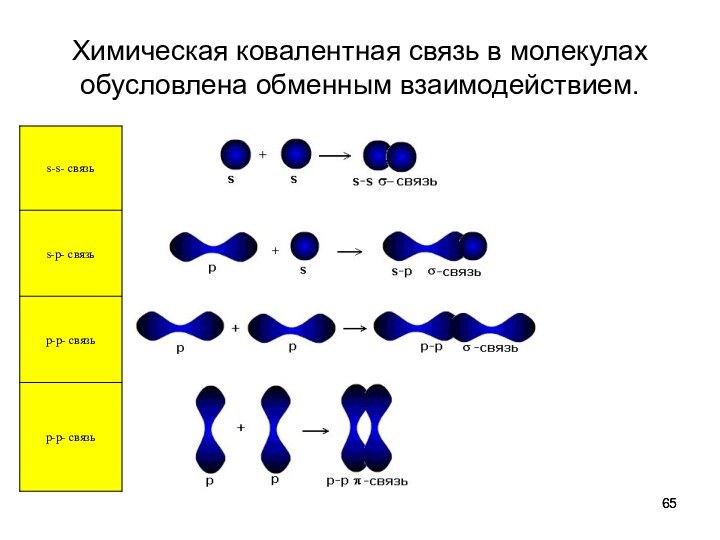
Химическая ковалентная связь в молекулах обусловлена обменным
взаимодействием.
Слайд 66
Помимо ковалентной связи, имеющей квантовую природу, существуют и
другие механизмы возникновения устойчивых молекул
Слайд 67
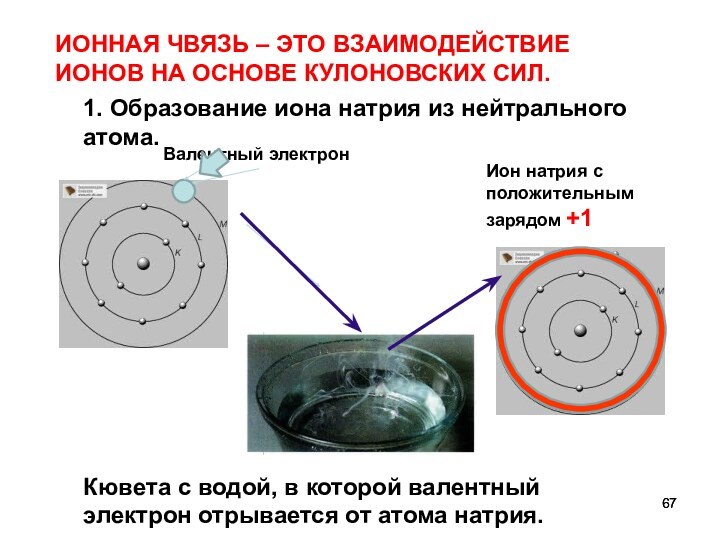
1. Образование иона натрия из нейтрального атома.
Валентный электрон
Ион
натрия с положительным зарядом +1
Кювета с водой, в которой
валентный электрон отрывается от атома натрия.
ИОННАЯ ЧВЯЗЬ – ЭТО ВЗАИМОДЕЙСТВИЕ ИОНОВ НА ОСНОВЕ КУЛОНОВСКИХ СИЛ.
Слайд 68
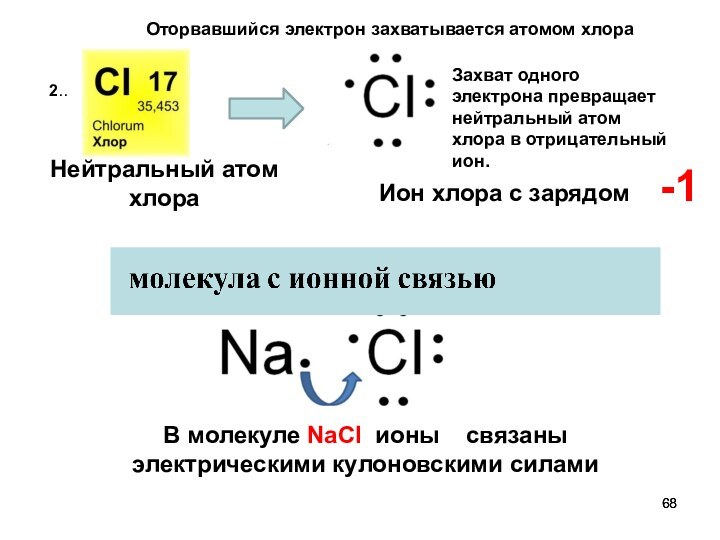
Нейтральный атом хлора
Ион хлора с зарядом -1
В
молекуле NaCl ионы связаны электрическими кулоновскими силами
Захват одного
электрона превращает нейтральный атом хлора в отрицательный ион.
2..
Оторвавшийся электрон захватывается атомом хлора
Слайд 69
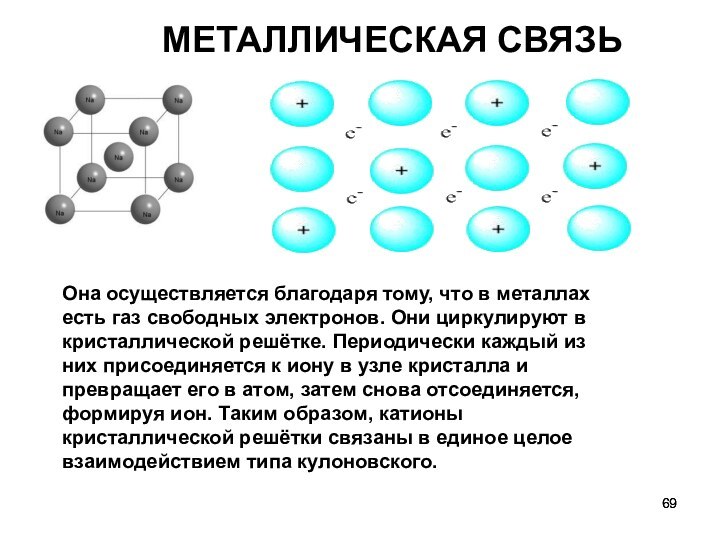
МЕТАЛЛИЧЕСКАЯ СВЯЗЬ
Она осуществляется благодаря тому, что
в металлах есть газ свободных электронов. Они циркулируют в
кристаллической решётке. Периодически каждый из них присоединяется к иону в узле кристалла и превращает его в атом, затем снова отсоединяется, формируя ион. Таким образом, катионы кристаллической решётки связаны в единое целое взаимодействием типа кулоновского.
Слайд 70
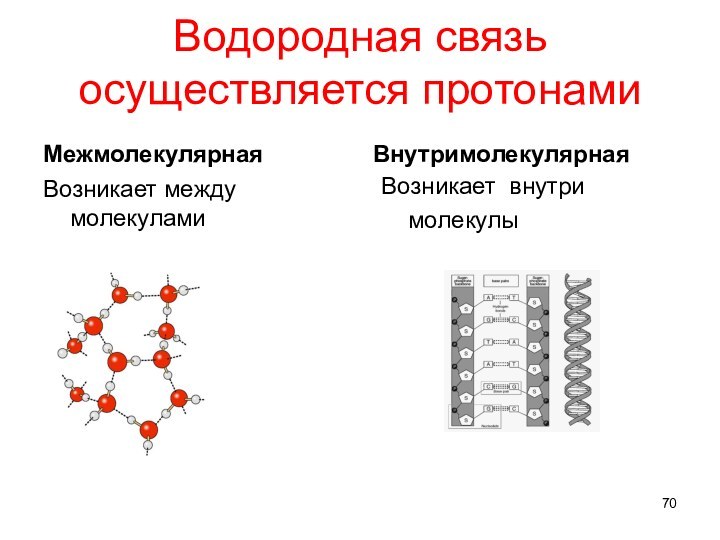
Водородная связь осуществляется протонами
Межмолекулярная
Возникает между молекулами
Внутримолекулярная
Возникает внутри
молекулы
Слайд 71
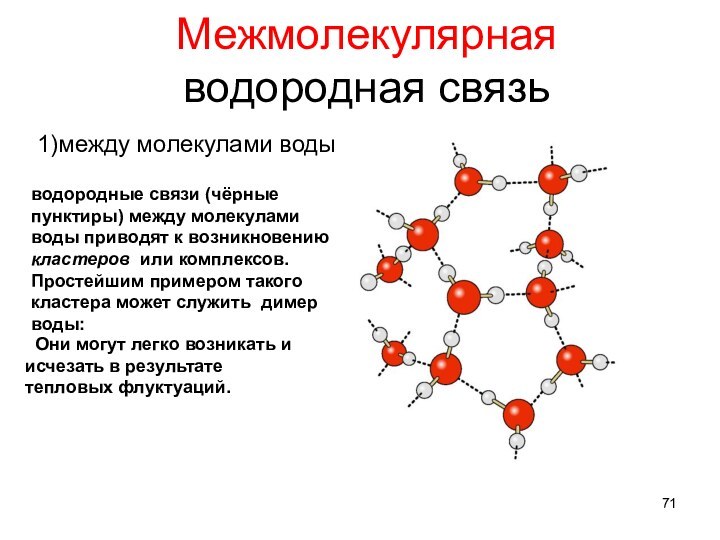
Межмолекулярная водородная связь
1)между молекулами воды
водородные связи (чёрные
пунктиры) между молекулами воды приводят к возникновению кластеров
или комплексов. Простейшим примером такого кластера может служить димер воды:
Они могут легко возникать и исчезать в результате тепловых флуктуаций.
Слайд 72
Межмолекулярные водородные связи способствуют образованию кристаллов в виде
снежинок или измороси
Слайд 73
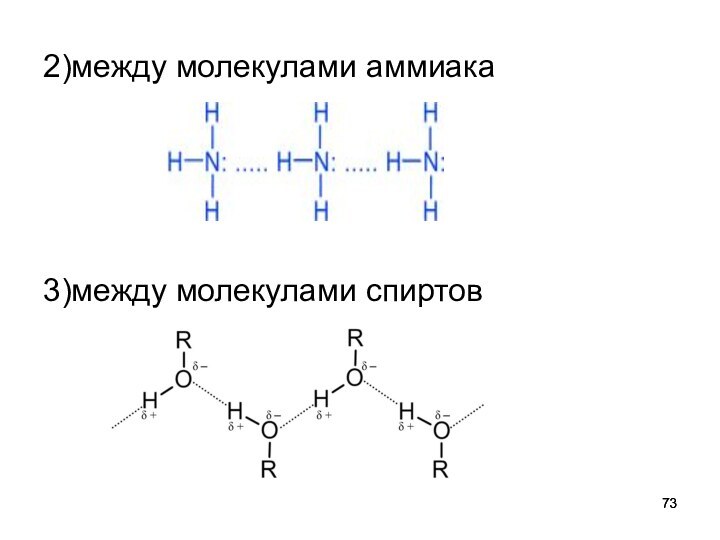
2)между молекулами аммиака
3)между молекулами спиртов
Слайд 74
Внутримолекулярная водородная связь
возникает
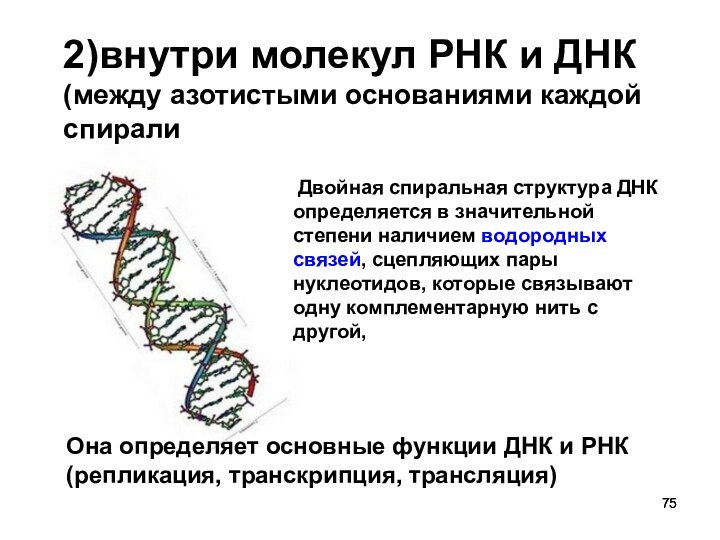
1)внутри молекул белков (водородная связь
удерживает витки спирали пептидной молекулы)