Презентация на тему Өлшеу қателіктері

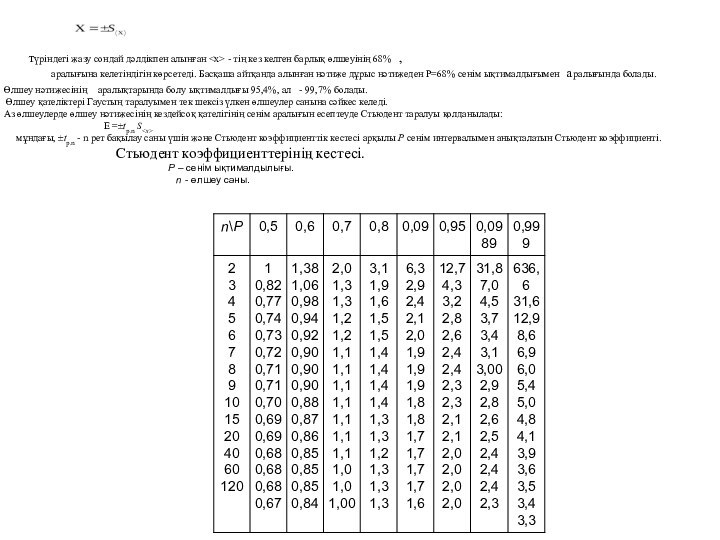
жуық нәтижесін береді және өлшеу қателіксіз болмайды.
Қандай да бір х физикалық

шаманы п рет өлшенді дейік, нәтижесінде осы шаманың х1, х2,… хn мәндер қатары алынды. Өлшеуді орындаған кезде, нәтижені біліп қана қоймай, оның дәлдігі жайлы хабардар болу керек. Көптеген жағдайларда х шамасының өлшем мәндері х1, х2… хn болғанда, бұл өлшеудің орташа арифметикалық нәтижесі <х> болып табылады. Бұл кезде өлшенген шама мәнінің интервалын ±Dx көрсету қажет;
<х> +Dx - өлшенген шаманың дәл үлкен мәні; <х>-Dx – дәл кіші мәні.
Dx шамасы өлшеу нәтижесінің қателігі немесе қателік деп аталады, ал <х>+Dx интервалыны мен <х>-Dx интервалына дейінгі аралық (сенімді) дәлме-дәл интервал делінеді. <х> - орташа мәнінің шындықтан айырмашылығы, ол Р-ның дәлме-дәл болуынан шығады. Ол бір тектес өлшеу түрлерінің нәтижелерінің үлесіне тең, яғни Dx шамасының шындықтан айырмашылығы сандық мәнінде болады. Сенім аралығы e- берілген Р ықтимал бойынша, <х> нүктесінде кесіндінің 2e сандық осі центрмен бірге өлшенетін хшаманың мәнін өзіне қосу арқылы анықталады.

шаманың дәл мәніне сәйкес келуі үшін үлкен Р ықтимал алынады. Бұл

жағдайда, ±e =kDxинтервалының аралығы қалыптасады, мұнда k коэффициенті Р/Р0 қатынасы бойынша анықталады.
k = Р/Р0
Егер құралдың көрсетуі бойынша өлшеу нәтижелерін қайта жөндеп, көп немесе аз қателіктерін тапсақ, онда өлшеудің жөнделген нәтижелерінің орташа арифметикалық мәні мына формула бойынша табылады:

Әдетте жалпы қабылданған өлшеудің стандарт қателіктерінің орнына орташа квадраттық қателіктер алынады. Ол өлшеу қателіктерінің жақсы жуықтайтын кездейсоқ шамалары үшін Гаусс анықтамасының дисперсиясына тең.
Өлшеу нәтижесінің орташа арифметикалық мәнінен алынған орташа квадраттық ауытқу мына формуламен анықталады:

Орташа квадраттық қателіктің ауытқуы S шамасының орташа арифметикалық қателігін түсіндіреді.

түріндегі жазу сондай дәлдікпен алынған <х> - тің кез келген барлық өлшеуінің 68%  , 
  аралығына келетіндігін көрсетеді. Басқаша айтқанда алынған нәтиже дұрыс нәтижеден Р=68% сенім ықтималдығымен  аралығында болады.
Өлшеу нәтижесінің   аралықтарында болу ықтималдығы 95,4%, ал  - 99,7% болады.
Өлшеу қателіктері Гаустың таралуымен тек шексіз үлкен өлшеулер санына сәйкес келеді.
Аз өлшеулерде өлшеу нәтижесінің кездейсоқ қателігінің сенім аралығын есептеуде Стьюдент таралуы қолданылады:
E =±tp.n S
мұндағы, ±tp.n - n рет бақылау саны үшін және Стьюдент коэффициенттік кестесі арқылы Р сенім интервалымен анықталатын Стьюдент коэффициенті.
Стьюдент коэффициенттерінің кестесі.
Р – сенім ықтималдылығы.
n - өлшеу саны.

қалатын қателік болып бөлінеді. Олар тәжірибе жүргізушінің анық зер

салмауынан болады (мысалы, өлшеуіш құрал арқылы дұрыс өлшемеу, санақты дұрыс жазбау және т.с.с.) Көп жағдайда, байқамай жіберілетін қателіктер көп ретті өлшеулер кезінде анық білінеді, себебі сәйкес санаудың басқалардан айырмашылықтары болады..

Өлшеу жұмыстарының сапасын анықтау үшін жуық мәндердің салыстырмалы қателіктерін қолданады.

см-ге тең
\АВ\ =3,3см

Мысалы:

табылады. Өлшеу дәлдігін арттыру мүмкін болатын қателіктердің көзін жою.

Шкаламен жұмыс жасаған кезде мұндай қателіктер шкаланың біркелкі болмауынан, шкала штрихтарының қалыңдығынан болуы және т.б. Барлық алынған өлшеу құралдарын дұрыстау қателік көздерін жою және шкала бөліктерін азайтумен шектеледі.
Штангенциркуль. Штангенциркуль бөліктерге бөлінген сызғыштан, араларына өлшенетін дене орналастырылған екі қысқаштан тұрады. Қысқыштың біреуі қозғалыссыз, онымен сызғыштың нөлдік санағы байланысады, екінші қысқыш сызғыш бойымен, дене өлшемі бойында сырғиды.

орын ауыстыруын ескеру қажет. Әдетте, ол микрометрлік бұранда көмегімен

болады. Микрометрлік бұранда – бұл үлкен диаметрлі және аз жүрісті бұранда. Бұранданың бір айналымы қысқыштың аз жүріске тең арақашықтығына орын ауыстырады. Үлкен диаметрдің көмегімен бұранданың шеңберін үлкен бөліктерге бөледі (50-100 бөліктерге) және бұранда айналымының бөлігін оның жүріс бөлігіне ауыстырады. Бұранданың 0,5 мм жүрісі және бұранда шеңберінің 50 бөлікке бөлінуі – бұл 0,01 мм. дәлдікпен қалыңдықты өлшеуге мүмкіндік береді. Микрометрлік бұранданың шкаласы әдетте нониуспен қамтамасыз етілмейді, себебі бұранданың жүрісінің дәл келмеуі және бұранда қысқышының (резьба) сапасы штрих қалыңдығына сәйкес келетін жүріс бөлігінен артық болады.