Слайд 2
План лекции
Виды зубчатых передач. Основные характеристики зубчатых передач.

Геометрия и кинематика эвольвентного зубчатого зацепления. Материалы и допускаемые
напряжения. Допускаемые контактные напряжения. Расчет зубчатого зацепления на контактную прочность. . Расчет зубьев на изгиб. Проектировочный расчет на контактную выносливость.
Зубчатые редукторы. Червячные передачи. Общие сведения. Классификация червячных передач. Верхнее и нижнее расположение червяка. Геометрия и кинематика червячного зацепления. Расчет червячного зацепления на контактную прочность. Расчет открытых червячных передач. Конструкции червяков и червячных колес.
Цепные передачи. Основные характеристики цепных передач, устройство и область применения. Основные геометрические параметры. Разрушающая нагрузка. Критерии работоспособности цепных передач.
Передача винт-гайка. Устройство и назначение передач винт-гайка. Силовые соотношения в винтовой паре. Привод винтовой передачи. Критерии работоспособности. Методика расчета передачи. Грузовой винтовой механизм. Расчет винтов и гаек передач на прочность.
Слайд 3
Виды цилиндрических зубчатых передач
Цилиндрические зубчатые передачи передают вращающий
момент между параллельными валами.
Прямозубые колёса (около 70%) применяют при
невысоких и средних скоростях, когда динамические нагрузки от неточности изготовления невелики, в планетарных, открытых передачах, а также при необходимости осевого перемещения колёс.
Слайд 4
Косозубые колёса (более 30%) имеют большую плавность хода
и применяются для ответственных механизмов при средних и высоких
скоростях.
Шевронные колёса имеют достоинства косозубых колёс плюс уравновешенные осевые силы и используются в высоконагруженных передачах.
Колёса внутреннего зацепления вращаются в одинаковых направлениях и применяются обычно в планетарных передачах.
Выбор параметров цилиндрических зубчатых передач обусловлен конструктивными и технологическими условиями.
Слайд 5
Передаточное отношение U определяется соотношением угловых скоростей (ω)
или частот вращения (n) ведомого и ведущего колёс
U = ω1 / ω2 = n1 / n2.
Здесь и далее индексы 1 и 2 расставлены в порядке передачи механической энергии 1- ведущее (шестерня), 2- ведомое (колесо). Учитывая, что в зацепление входят колёса с одинаковым модулем (, можно задавшись числом зубьев шестерни Z1 найти число зубьев колеса
Z2 = U * Z1.
Передаточное число U ограничено габаритами зубчатой передачи.
Слайд 6
Основные характеристики зубчатых передач
Расчетная окружная скорость м/с
цилиндрической зубчатой передачи
Конической передачи
где - угловая скорость зубчатого
колеса,
n- частота вращения зубчатого колеса, мин-1
dw- начальный диаметр цилиндрического зубчатого колеса, м
dwm- начальный средний диаметр конического зубчатого колеса
Слайд 7
Учитывая, что скорость точек начальных окружностей, находящихся в
зацеплении зубчатых колес, одинаково, имеем
Выражая диаметр через модуль зацепления
и соответствующее число зубов, получаем
Отсюда передаточное отношение пары зубчатых колес (для одноступенчатой передачи)
где T1 и T2 - крутящий момент ведущего и ведомого колеса .
Отношение числа зубьев Z2 колеса и числа зубьев Z1, шестерни называют передаточным числом зубчатой передачи .
Слайд 8
Окружная сила цилиндрической зубчатой передачи определяется по формуле
Окружная сила конической зубчатой передачи определяется по формуле
Слайд 9
Геометрия эволентного зубчатого зацепления
Модуль зубьев m
m = p/π
= d/z
Высота зуба h
h = 2,25m
3. Высота головки
зуба ha
ha = m
4. Высота ножки зуба hf
hf = 1,25m
Диаметр делительной окружности d
d = mz
Слайд 10
Модуль зубьев m
m = p/π = d/z
Высота зуба
h
h = 2,25m
3. Высота головки зуба ha
ha =
m
4. Высота ножки зуба hf
hf = 1,25m
Диаметр делительной окружности d
d = mz
6. Диаметр окружности
Выступов da
da = d + 2ha = d+2m
7.Диаметр окружности
впадин df
= d — 2hf = d — 2,5m
8. Радиальный зазор между сопряженными колесами с
с = 0,25m
9. Межосевое расстояние aω
aω=
Слайд 11
10. Шаг зубьев p
p =π/m
11. Толщина зуба st
st
= 0,5p
12. Ширина впадины e
e = 0,5p
13. Ширина
венца зубчатого колеса
(длина зуба) b
b ≈ (6...8)m
14. Диаметр ступицы dCT
dCT ≈ (l,6...2)dB1)
15. Длина ступицы Lcr
LCT ≈ 1.5dB
16. Толщина обода δ
δ ≈ (2,5...4)m
Слайд 12
Материалы и допускаемые напряжения
Зубчатые колеса изготовляют из сталей,
чугуна и неметаллических материалов. Колеса из неметаллических материалов имеют
небольшую массу и не корродируют, а передачи с ними бесшумны в работе. Но невысокая прочность материалов и, как следствие, большие габариты передачи и сравнительно высокая стоимость изготовления колес ограничивают их применение в силовых механизмах.
Чугунные зубчатые колеса дешевле стальных, их применяют в малонагруженных открытых передачах. Они имеют малую склонность к заеданию и хорошо работают при бедной смазке, но не выдерживают ударных нагрузок.
Слайд 13
Допускаемые напряжения.
Допускаемые напряжения изгиба при расчете на выносливость
определяют по формуле
Где σFlim — предел выносливости зубьев, соответствующий
заданному (установленному) числу циклов нагружений; SF— коэффициент безопасности (допускаемый запас прочности); YS= 1,08—0,16lgm— коэффициент, учитывающий влияние абсолютных размеров зубьев; KxF=( 1 — 8,3X 10-5)da—то же, для колес (da — диаметр вершин колеса, мм; m — модуль, мм); YR — коэффициент, учитывающий влияние шероховатости поверхности (при полировании переходной поверхности равен 1.05÷1,2).
Слайд 14
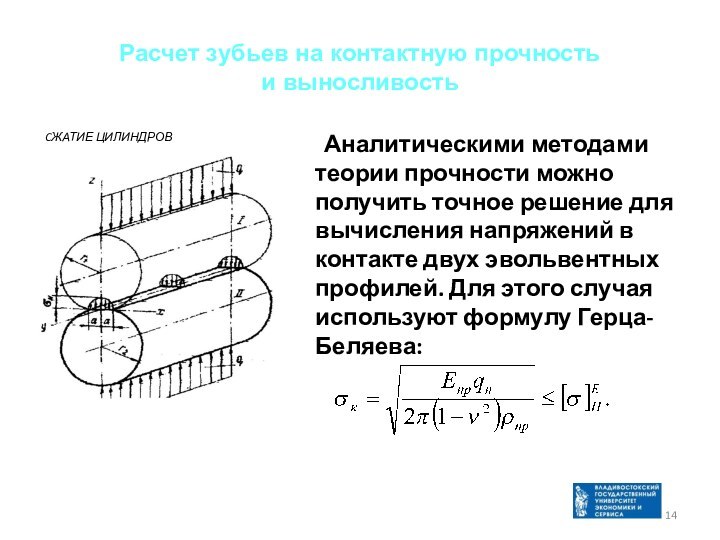
Расчет зубьев на контактную прочность
и выносливость
Аналитическими методами
теории прочности можно получить точное решение для вычисления напряжений
в контакте двух эвольвентных профилей. Для этого случая используют формулу Герца-Беляева:
Слайд 15
Здесь Епр – приведённый модуль упругости материалов шестерни
и колеса
Епр = 2 Е1 Е2 / ( Е1
+ Е2),
пр – приведённый радиус кривизны зубьев
1/пр = 1/1 1/2, 1,2 = 0,5dW 1,2 sin W ,
- коэффициент Пуассона, qn - удельная погонная нормальная нагрузка, []HE - допускаемые контактные напряжения с учётом фактических условий работы.
Слайд 16
Расчёт зубьев на контактную выносливость для закрытых передач
(длительно работают на постоянных режимах без перегрузок) выполняют как
проектировочный. В расчёте задаются передаточным отношением, которое зависит от делительных диаметров и определяют межосевое расстояние Аw (или модуль m), а через него и все геометрические параметры зубьев. Для открытых передач контактные дефекты не характерны и этот расчёт выполняют, как проверочный, вычисляя контактные напряжения и сравнивая их с допускаемыми.
Слайд 18
Напряжения сжатия вычитаются из напряжений изгиба. Учитывая, что
напряжения изгиба в консольной балке равны частному от деления
изгибающего момента Mизг на момент сопротивления корневого сечения зуба W, а напряжения сжатия это сила Fr, делённая на площадь корневого сечения зуба, получаем:
.
Здесь b – ширина зуба, m – модуль зацепления,
YH – коэффициент прочности зуба.
Слайд 19
Зубчатые редукторы
Редуктором называют механизм, состоящий из зубчатых или
червячных передач, выполненный в виде отдельного агрегата и служащий
для передачи вращения от вала двигателя к валу рабочей машины.
Назначение редуктора — понижение угловой скорости и соответственно повышение вращающего момента ведомого вала по сравнению с ведущим.
Редуктор состоит из корпуса (литого чугунного или сварного стального), в котором помещают элементы передачи — зубчатые колеса, валы, подшипники и т. д.
Слайд 20
Примеры цилиндрических зубчатых редукторов
Рис. 1. Одноступенчатый горизонтальный
редуктор с цилиндрическими зубчатыми колесами:
а — кинематическая
схема; б - общий вид редуктора с косозубыми колесами
Слайд 21
Рис. 2. Двухступенчатый горизонтальный редуктор с цилиндрическими колесами:
а
— кинематическая схема; б — редуктор
со снятой крышкой (колеса косо-
зубчатые); в — общий вид редуктора, у которого подшипниковые узлы закрыты
врезными крышками; г — общий вид редуктора, у которого подшипниковые
крышки привернуты винтами
Слайд 22
Рис. 3. Двухступенчатый горизонтальный
редуктор с раздвоенной первой (быстроходной) ступенью:
«-кинематическая
схема; б - общий вид (без крышки)
Слайд 23
Червячные передачи и передачи винт-гайка
Основы проектирования
червячных передач и винтовой передачи (винт-гайка) рассмотрены в теме
3 данной презентации.
Слайд 24
Цепные передачи
Основные характеристики цепных передач, устройств и область
применения
Рис.1.
Схема цепной передачи
Цепными называют передачи с помощью цепей.
Слайд 25
Передача (рис. 1) состоит обычно из ведущей 1
и ведомой 2 звездочек, связанных между собой приводной цепью
(в машиностроении применяют
также грузовые и тяговые цепи). Их применяют в качестве ступеней в приводах стационарных механизмов и машин (станках, роботах, сельскохозяйственной, транспортной технике и др.).
Числа зубьев z1 и z2 звездочек выбирают из условия обеспечения минимальных габаритов и более плавного хода цепи.
Расстояние а между осями звездочек (см. рис. 1) также влияет на работоспособность цепи, так как оно определяет частоту нагружения шарниров. При малом а цепь быстро изнашивается, а при большом а ведомая ветвь начинает колебаться из-за сильного провисания.
Слайд 26
На практике стремятся к тому, чтобы
а=(30>50)t.
Минимальное значение а
ограничивают обхватом цепи (amin≥120°): при i≤3
amin = 0,5(d1+ d2)
+ (30÷50) мм; при i>3
Потребное число звеньев цепи (длина цепи в шагах) определяется по предварительно выбранным значениям a, t, z1 и z2:
Для обеспечения нормального провисания ведомой ветви цепи межосевое расстояние уменьшают на 0,2—0,4%.
Слайд 27
Критерии работоспособности цепных передач
Износ шарниров в процессе эксплуатации
— типичный вид повреждения цепей быстроходных закрытых и полузакрытых
передач станков,
двигателей и оборудования общего машиностроения.
Усталостное разрушение элементов цепи вызывается переменными напряжениями от внешней нагрузки, сил инерции и ударных нагрузок, обусловленных внутренней динамикой цепного привода. Разрушению часто предшествует контактная коррозия, развивающаяся на стенках отверстий пластин и на поверхностях роликов и осей.
Слайд 28
При скоростях vц>15 м/с возрастают ударные нагрузки в
передаче, и даже при сравнительно небольших нагрузках может происходить
раскалывание роликов и ослабление прессовых соединений валиков и втулок с пластинками.
Таким образом, износостойкость и прочность цепей являются основными критериями работоспособности передач.